0

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ,

СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»

(СПбГУТ)

Факультет Инфокоммуникационных сетей и систем

Кафедра Защищенных систем связи

Дисциплина Криптографические протоколы

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №0

Изучение криптосистем с открытыми ключами на основе эллиптических кривых

(тема отчета)

Направление/специальность подготовки

10.03.01 Информационная безопасность

(код и наименование направления/специальности)

Выполнил студент 3 курса:

Травкина Е.А., ИКБ-14

(Ф.И.О., № группы) (подпись)

Преподаватель:

д.т.н., проф. Яковлев В.А.

(Ф.И.О., № группы) (подпись)

Цель работы:

Приобретение навыков анализа алгоритмов криптосистем с открытыми ключами на основе эллиптических кривых.

Ход работы:

Вариант 19.

	Задано				Найти
Nвар	A	B	k	C		-C	kC
19	4,11	8,1	4

Задание 1.

Задана эллиптическая кривая Е13(1,1) в поле GF(13) по уравнению . (Уравнение вида , где a=1, b=1.)

Точки Е13(1,1) (без нулевой точки) представлены на рис.1.

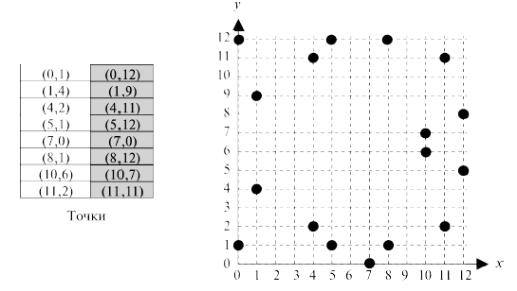
Рис. 1. Точки и граф эллиптической кривой

Проверка принадлежности точек заданной кривой:

Так как x=y, то точка B принадлежит заданной кривой.

A(4,11)	:
	:

Так как x=y, то точка A принадлежит заданной кривой.

В(8,1)	:
	:

Так как x=y, то точка В принадлежит заданной кривой.

Взаимообратные точки:

A(4;11)	→	A’(4;2)
В(8;1)	→	В’(8;12)

Вычисления:

1. Найдем точку C по формуле

Так как A≠B, то

Ищем обратный элемент



,

2. Поиск противоположной точки C

3. Умножение на константу k=4

1. 

Так как С=С, то

Ищем обратный элемент



,

2. 

Так как R=R, то

Ищем обратный элемент



,

3. и

Так как С≠Q, то

Ищем обратный элемент





, 1

,

Задание 2.

Моделирование криптосистемы Эль-Гамаля на эллиптической кривой

Вариант 19.

	Задано			Вычислить
Nвар	d	r	E1		E2	C1	C2
19	5	1

1. Записать уравнение кривой Е₆₇(2,N), где N номер варианта.

– кривая, – уравнение кривой

2. Выбрать точку Е₁. Проверить ее принадлежность кривой.

Пусть Е₁ (4,15). 15² = 4³ +2*4+19 (mod 67) → 225 = 91 (mod 67) → 24=24 →Точка E принадлежит кривой y² = x³ + 2x+19

3. Вычислить точку Е₂ = d*E₁ (d=5 согласно варианту)

E₂ = 5*E₁= (34,14) (см. Рисунок 2.)

Рисунок 2. Умножение точки Е₁ на 5.

1. Передаем E₆₇(2,19), E₁(4,15) и E₂(34,14) корреспонденту В, в качестве открытого ключа, параметр d-закрытый ключ (не передается).

2. Выбираем произвольную точку P(9,30) (900=766 mod 67 → 29=29 → точка принадлежит кривой) и r – r =1.

3. Высчитать C₁=r*E₁= 1*Е₁(4,15) (см. Рисунок 3.)

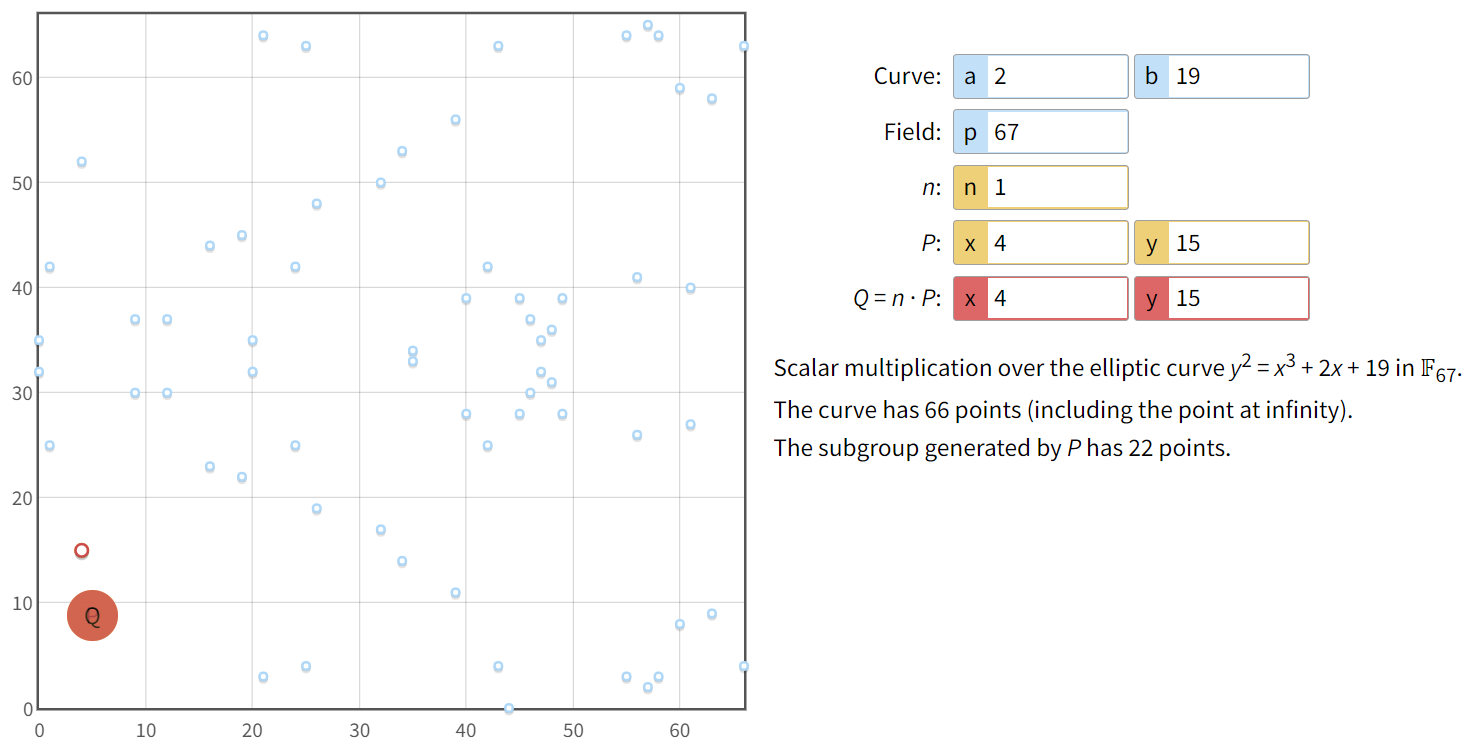
Рисунок 3. Умножение r на E₁.

4. Высчитать С₂ = P(9,30)+1*E₂(34,14) = (38,33) (cм. Рисунок 4-5.)

Рисунок 4. Умножение r на E2.

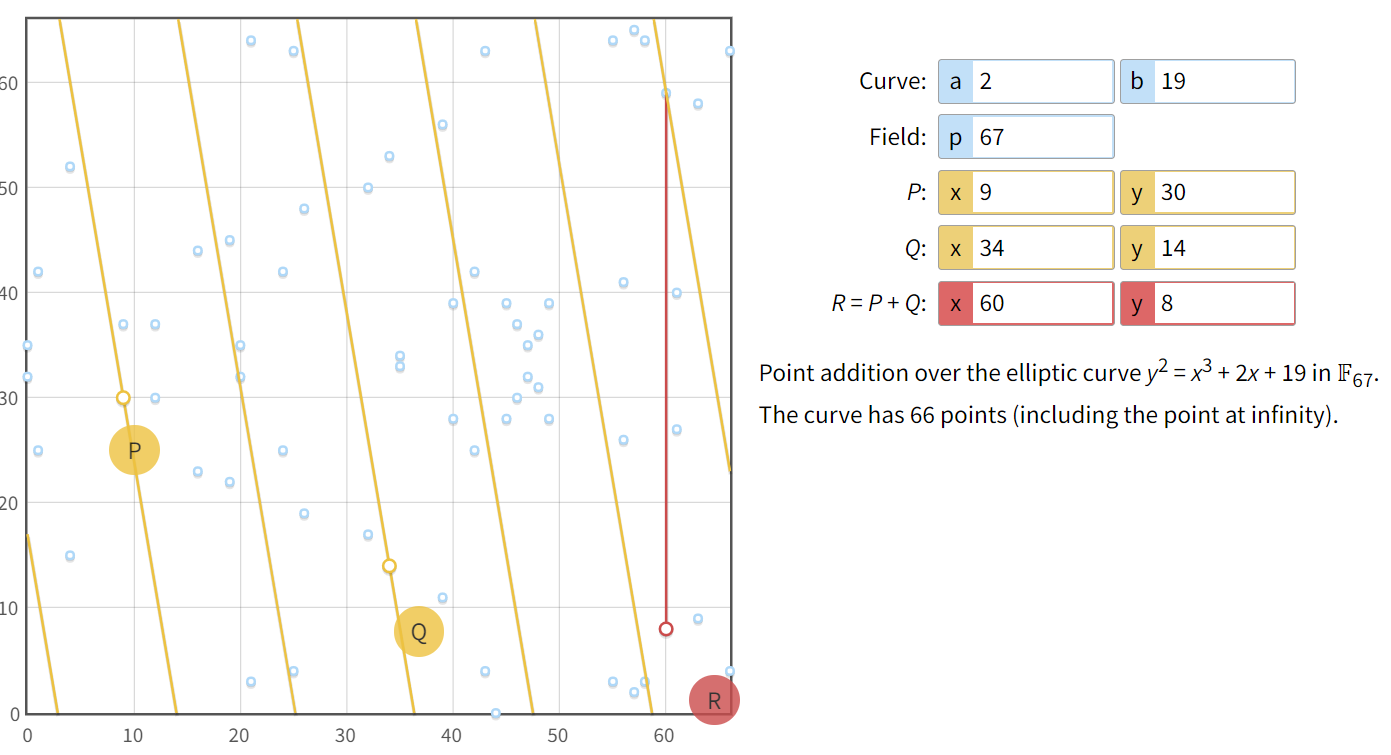
Рисунок 5. Значение точки С2.

5. P=C2-(d*C1) = (60,8)-(34,14)

Инверсной точкой к точке (34,14) будет (34,67-14) = (34,53), следовательно

P=(60,8)+(34,53)=(9,30) (см. Рисунок 6-7)

Переданное сообщение при расшифровке совпадает с изначальным.

Рисунок 6. Умножение d на C1.

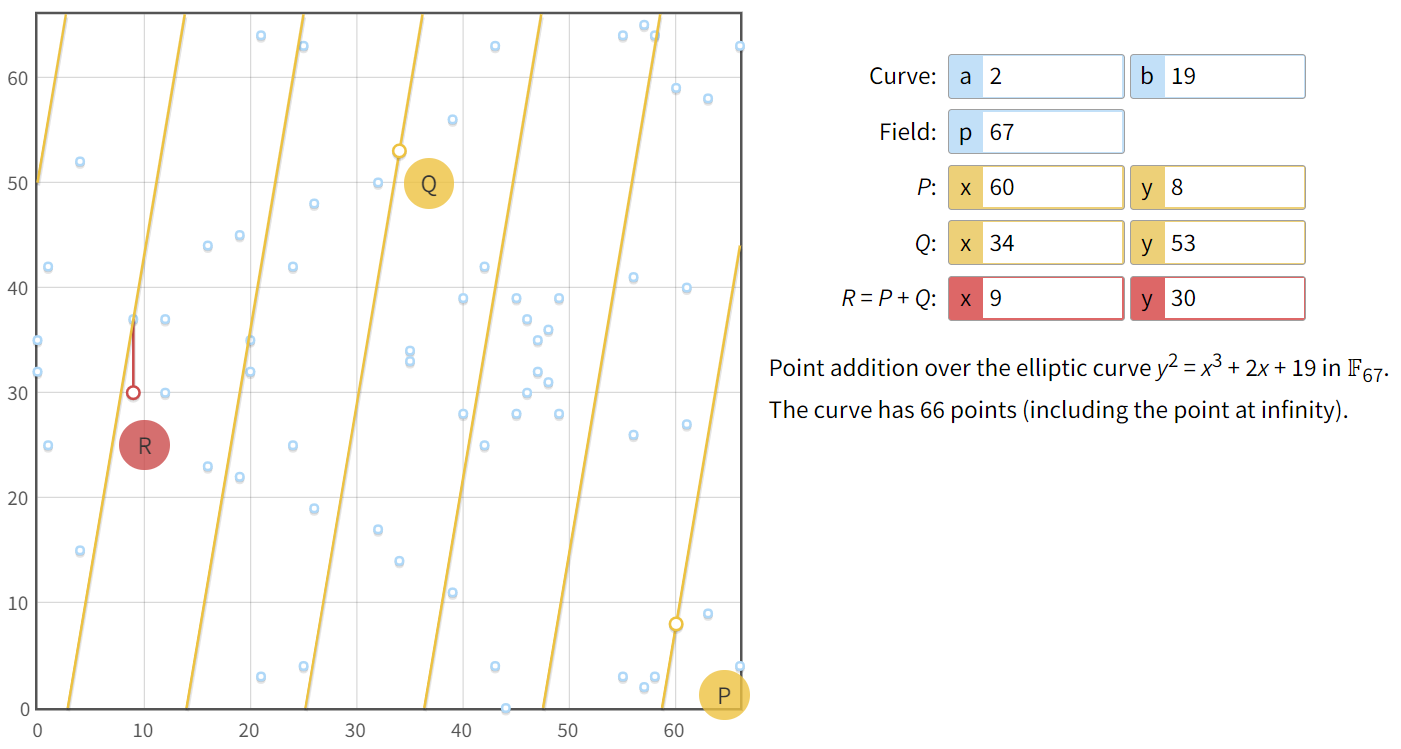
Рисунок 7.Вычисление сложения точки с инверсной.

Вывод:

В ходе выполнения практического задания мы приобрели навыки вычислений с использованием матаппарата эллиптических кривых. Провели моделирование криптосистемы Эль-Гамаля на основе эллиптической кривой.

Санкт-Петербург

2023