Расчет электрических цепей в Smath Studio (учебное пособие)

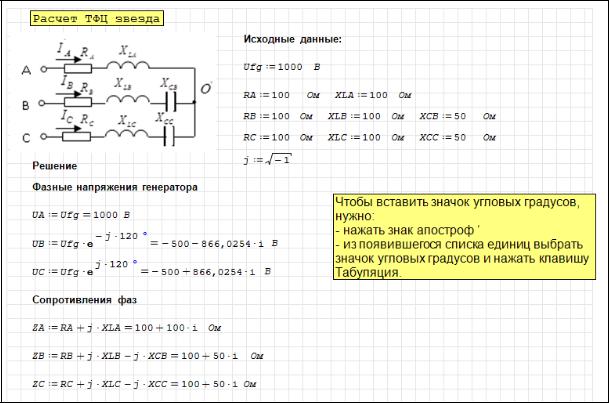
При построении обязательно выдержить масштаб по мнимой и действительной осям одинаковым. Так, на рисунке 2.31, ячейки полотна графика представляют собой квадраты со стороной 256 В в масштабе. Если масштаб будет разным по осям, то вектора UA, UB, UC не образуют трехфазную симметричную систему на диаграмме. Для звезды векторов токов,

изображенной на рисунке 2.31 красным цветом, масштаб увеличен в 80 раз.

Коэффициент масштабирование выбирается в зависимости от полученных результатов. Так как на одном полотне необходимо построить несколько графиков необходимо выбрать знак системы с панели инструментов Функции

и увеличить размерность системы, нажимая на клавиатуре <;>.

На рисунках 2.32 - 2.35 показан расчет трехфазной цепи при соединении приемника звездой.

Рисунок 2.32 – Расчет фазных сопротивлений

71

Рисунок 2.33 – Расчет фазных напряжений на нагрузке

Рисунок 2.34 – Расчет фазных токов и баланс мощностей

72

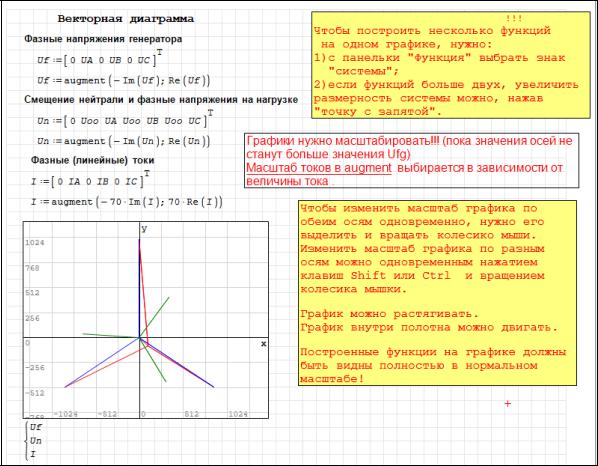
Рисунок 2.35 – Векторная диаграмма при соединении нагрузки звездой

Особенностью векторной диаграммы при соединении несимметричной нагрузки звездой является построение вектора напряжения смещения нейтрали.

Построение начинаем с симметричной трехфазной системы напряжений генератора (источника), это три вектора одинаковой длины строятся из начала координат под угол 1200 (на рисунке 2.35 изображены синим цветом). Затем записываем матрицу-строку для фазных напряжений нагрузки, которые строятся из конца вектора напряжения смещения нейтрали (на рисунке 2.35

изображены красным цветом). Так две звезды напряжений связаны друг с другом, их строят в одном масштабе. Для звезды векторов токов, на рисунке

2.35 изображены зеленым цветом, масштаб увеличен в 70 раз. Коэффициент масштабирование выбирается в зависимости от полученных результатов.

73

Расчет трехфазной цепи при соединении нагрузки треугольником показан на рисунках 2.36 – 2.39.

Рисунок 2.36 – Расчет напряжений

Рисунок 2.37 – Расчет фазных токов

74

Рисунок 2.38 – Расчет линейных токов и баланс мощностей

На рисунке 2.39 представлено построение векторной диаграммы при соединении несимметричной нагрузки треугольником. Построение начинаем с симметричной трехфазной системы напряжений генератора (источника), это три вектора одинаковой длины строятся из начала координат под угол 1200 (на рисунке 2.39 изображены синим цветом). Затем записываем матрицу-строку для линейных напряжений генератора, которые являются фазными напряжениями нагрузки, так как нагрузка соединена треугольником. В матрице строке последовательно указываем точки, которые должны быть соединены. В

результате получаем равносторонний треугольник линейныхъ напряжений (на рисунке 2.39 изображены красным цветом). Звезда фазных напряжений и треугольник линейных напряжений связаны друг с другом, их строят в одном масштабе. Аналогично записываются матрицы строки для построения токов.

Фазные токи строятся из начала координат (на рисунке 2.39 изображены зеленым цветом), а линейные токи образуют треугольник (на рисунке 2.39

изображены розовым цветом). Для векторов токов масштаб увеличен в 50 раз.

Коэффициент масштабирование выбирается в зависимости от полученных результатов и должен быть одинаковым и для фазных, и для линейных токов.

75

Так как на одном полотне необходимо построить несколько графиков необходимо выбрать знак системы с панели инструментов Функции и

увеличить размерность системы, нажимая на клавиатуре <;>.

Рисунок 2.39 – Векторная диаграмма при соединении нагрузки треугольником

2.5 Метод симметричных составляющих

Для анализа и расчета несимметричных режимов в трехфазных цепях широко применяется метод симметричных составляющих [6]. В основе метода лежит представление любой трехфазной несимметричной системы величин суммой трех симметричных трехфазных систем. На рисунках 2.40 -2.45 представлен расчет аварийного режима, короткого замыкания в фазе А на землю, в SMath

76

Studio. В данном разделе используются описанные выше возможности работы в SMath Studio с комплексными числами, матрицами и построение двумерного графика.

Рисунок 2.40 – Расчет параметров схемы замещения при поперечной несимметрии

Следует отметить, что при продольной несимметрии расчет будет аналогичным по использованию возможностей SMath Studio, но формулы будут иметь другой вид [6]. Единицы измерения, также как и в предыдущих примерах, набираются с помощью клавиатуру, вне области переменной. На рисунке 2.41. Записана система шести уравнений, составленных на основании метода симметричных составляющих. Три нижних уравнения описывают вид повреждения, в нашем случае, короткое замыкание фазы А на землю.

77

Рисунок 2.41 – Решение системы уравнений

Рисунок 2.42 – Симметричные составляющие. Определение токов в месте аварии

78

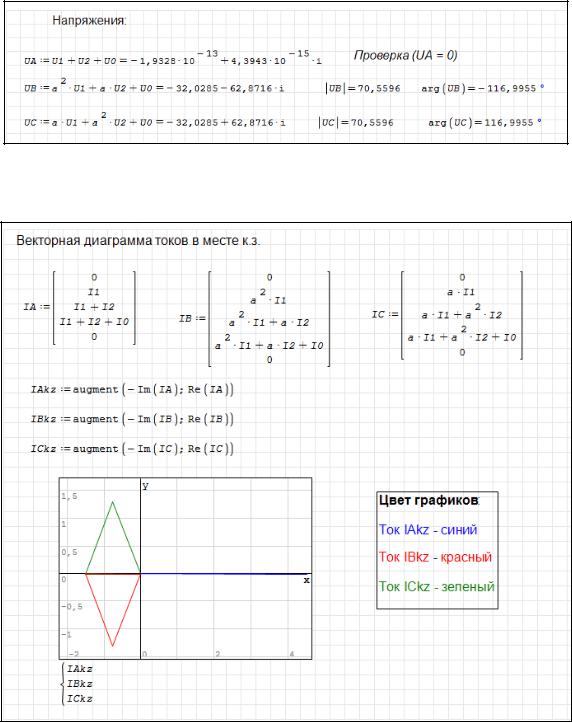
Рисунок 2.43 – Определение напряжений в месте аварии

Рисунок 2.44 – Векторная диаграмма токов в месте аварии

При построении векторной диаграммы, рисунок 2.44, выдерживаем масштаб по действительной и мнимой оси одинаковым. Так как и при расчете трехфазных цепей комплексная плоскость повернута на 900 , поэтому мнимую часть записываем со знаком минус.

79

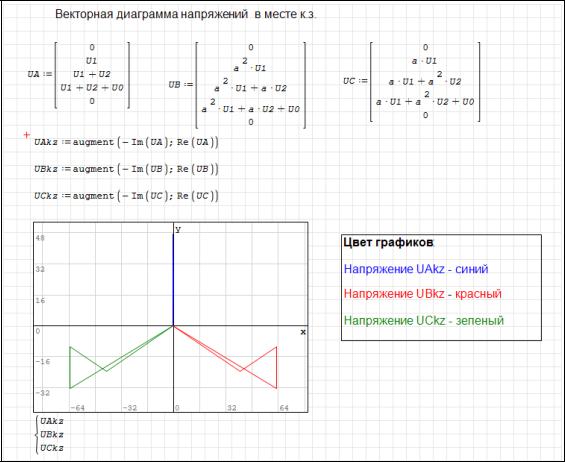
Рисунок 2.45 – Векторная диаграмма напряжений в месте аварии

2.6 Магнитные цепи

При анализе нелинейных электрических и магнитных цепей, в которых нелинейные характеристики элементов в основном задаются совокупностью табличных значений широко используется интерполяция. SMath Studio

позволяет использовать помимо линейной интерполяции интерполяцию сплайнами. При этом следует учитывать, что на заданном отрезке при любой интерполяции получаются близкие значения функции, а вот за пределами заданных отрезков данных значения при линейной интерполяции и интерполяции сплайнами будут сильно различаться. Рассмотрим пример расчет магнитной цепи при постоянных магнитных потоках в SMath Studio методом двух узлов.

80