
Расчет электрических цепей в Smath Studio (учебное пособие)
.pdf
1.9 Производные и интегралы
Производные. SMath Studio позволяет вычислять производные первого и высших порядков, их численные (в заданной точке) и аналитические значения.
Чтобы вычислить производную первого порядка в SMath Studio, можно воспользоваться кнопкой  на панели инструментов <Функции> или набрать с клавиатуры diff и во всплывающей подсказке выбирать diff(2), или использовать меню <Вставка><Функция> и функцию diff(2).
на панели инструментов <Функции> или набрать с клавиатуры diff и во всплывающей подсказке выбирать diff(2), или использовать меню <Вставка><Функция> и функцию diff(2).
Чтобы получить результат в виде функции (в символьном виде),
необходимо:
– задать функцию;
– вызвать оператор дифференцирования с панели «Функции» или с клавиатуры diff(2) , на экране появится шаблон оператора производной с двумя метками-заполнителями ;
–на месте переменной (черный квадратик внизу шаблона) ввести имя переменной, по которой производится дифференцирование (например, х), а
на месте функции (черный квадратик в правой части шаблона) ввести имя функции (или саму функцию);
–нажать кнопку  – оператор символьного вычисления на панели
– оператор символьного вычисления на панели
«Арифметика», результат будет выведен в символьном виде (в виде функции), рисунок 1.23.
Рисунок 1.23 – Пример дифференцирования функции в символьном виде
Для дифференцирования функции можно использовать также операцию
«Дифференцировать» из вкладки Главного меню «Вычисление». В этом
31
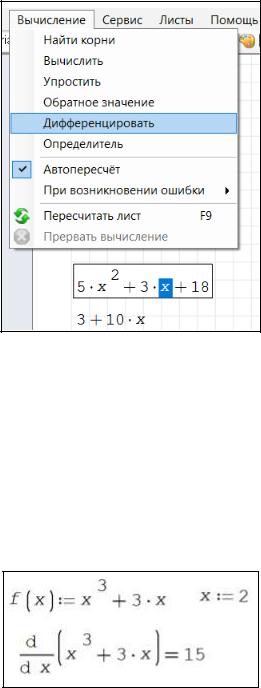
случае нужно в формуле функции выделить переменную дифференцирования и нажать «Дифференцировать», рисунок 1.24. Результат в виде формулы появится ниже.
Рисунок 1.24 – Выбор опции «Вычисление–Дифференцировать»
Чтобы найти значение производной функции в заданной точке,
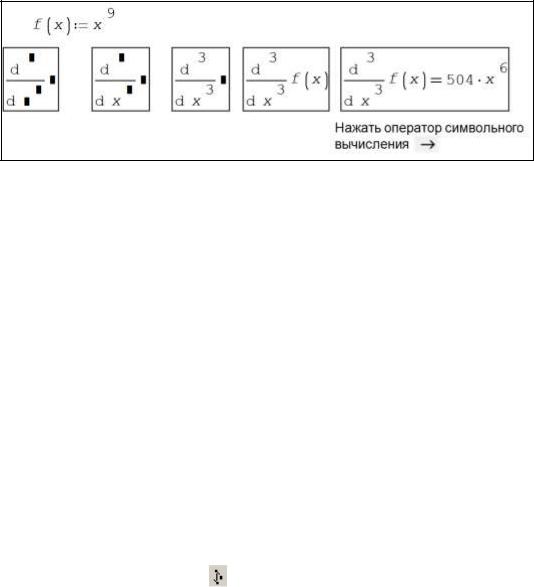
необходимо перед нахождением производной присвоить переменной дифференцирования заданное значение, рисунок 1.25.
Рисунок 1.25 – Нахождение производной в заданной точке
Для нахождения производных второго и более высоких порядков нужно с клавиатуры или из меню <Вставка><Функция> ввести функцию diff(3).
32
На экране появится шаблон оператора производной с четырьмя метками-
заполнителями. Здесь помимо функции и переменной дифференцирования нужно ввести порядок производной (он вводится в знаменателе, в числителе появится автоматически). Пример последовательности действий при нахождении производной, например, третьего порядка показан на рисунке
1.26.
Рисунок 1.26 – Последовательность действий при дифференцировании высокого порядка
Интегралы. В SMath Studio можно вычислить только определенные
интегралы.
Чтобы вычислить интеграл в SMath Studio, можно воспользоваться кнопкой 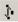 на панели инструментов <Функции> или набрать с клавиатуры
на панели инструментов <Функции> или набрать с клавиатуры
int и во всплывающей подсказке выбрать эту функцию, или использовать меню <Вставка><Функция> и функцию int.
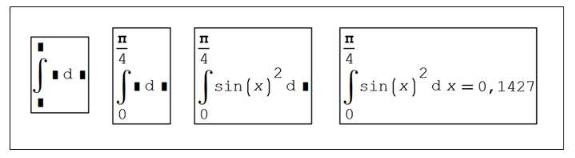
Например, определим интеграл функции |
sin2( x ) в интервале от 0 до |
||
/4. Для этого: |
|
|
|
– щелкаем мышью значок |
на панели инструментов <Функции>, |
либо |
|
выбираем стандартную функцию int с |
клавиатуры или из |
меню |
|
<Вставка><Функция>. |
|
|
|
– в появившемся символе интеграла, с метками-заполнителями заполняем пределы интегрирования, подынтегральное выражение, переменную
33
интегрирования;
– нажимаем знак = для получения результата, рисунок 1.27.
Рисунок 1.27 – Последовательность действий при интегрировании
1.10 Решение уравнений
Для решения уравнений в SMath Studio существуют встроенные функции, представленные в таблице 1.6.
Таблица 1.6
solve(2) |
Возвращает |
|
действительные |
||||
solve(<уравнение>; <переменная>) |
корни |
уравнения |
относительно |
||||
указанной переменной. |
|
|
|
||||
|
|
|
|
||||
solve(4) |
Возвращает |
|
действительные |
||||
solve(<уравнение>; <переменная>; |
корни уравнения |
внутри промежутка |
|||||
между a и b относительно указанной |
|||||||
|
|||||||
a;b) |
переменной. |
|
|
|
|
||
|
|
|
|
||||
|
Возвращает |
корни |
полинома, |
||||
polyroots(v) |
заданного |
вектором |
(v) |
его |
|||
коэффициентов. Может использоваться |
|||||||
|
|||||||
|
для нахождения как действительных, |
||||||
|
так и комплексных корней |
|
|
||||
Функция solve предназначена для решения отдельных уравнений только с действительными корнями. Уравнение может быть как линейным, так и нелинейным. В SMath Studio представлены два варианта функции solve: с
двумя solve(2) и с четырьмя solve(4) аргументами.
34
При использовании solve(2) необходимо помнить, что диапазон, в
котором программа будет искать корни, ограничен диапазоном, который установлен во вкладке «Опции» – «Вычисление» – «Корни (диапазон)». По умолчанию этот диапазон установлен от (–20) до (+20), но его можно менять.
Функция solve(4) позволяет сразу задать диапазон, в котором следует искать корни уравнения. Если в пределах заданного диапазона решение не найдено, то уравнение не будет решено, останется выделено красной рамкой,
при наведении курсора появляется надпись «действительных корней нет».
Если часть корней находится за пределами заданного диапазона, программа выдаст неполный список корней. Границы локализации корней называют начальными условиями и обычно рекомендуют определять перед решегтем графически.
Уравнение в функции solve можно задать следующими способами:
– как имя функции, которое заранее задано, например, f (x): 2x+10; solve(f (x); x);
– непосредственно уравнением без правой части, например, solve(2x+10; x);
– уравнением с правой частью, где вместо знака обычного равно ставится так называемое булево (или «жирное») равно с панели «Булева»,
например, solve(2ex=5x+2; x).
Примеры нахождения корней уравнений с помощью функции solve
показаны на рисунке 1.28.
35

Рисунок 1.28 – Использование функции solve |
для решения уравнений |
|
||||||
Для |
нахождения |
|
корней |
полинома |
степени |
n |
||
f (x) a xn a |
xn 1 ... a x1 |
a |
целесообразно |
использовать функцию |
||||
n |
n 1 |
1 |
0 |
|
|
|
|
|
polyroots. Данная функция не требует начального приближения и возвращает корни сразу, действительные или комплексные. Коэффициенты полинома должны быть заданы в виде вектора, начиная со свободного члена. Примеры нахождения корней уравнений с помощью функции polyroots показаны на рисунке 1.29.
Рисунок 1.29 – Использование функции polyroots для решения уравнений
В SMath Studio существует еще один способ, которым можно решить уравнение с действительными корнями, с помощью команды «Найти корни»
36
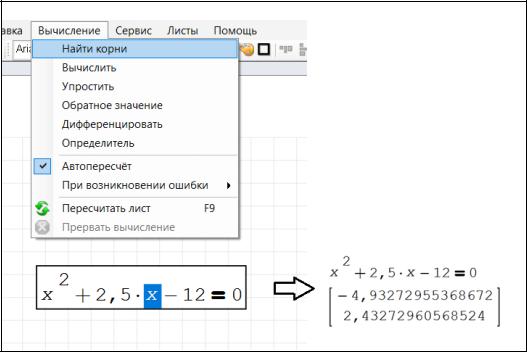
во вкладке меню «Вычисление». Для этого в уравнении нужно выделить курсором переменную и в меню выбрать «Вычисление Найти корни».
После этого под уравнением появятся найденные корни, рисунок 1.30.
Рисунок 1.30 – Нахождение корней через «Вычисление Найти корни»
При этом, независимо от предустановленной точности, корни рассчитаются с точностью 15 знаков. По умолчанию диапазон, в котором будут искаться корни, установлен от (–20) до (+20). При необходимости его можно изменить во вкладке «Сервис → Опции».
1.11 Решение систем уравнений
Для решения систем линейных алгебраических уравнений (СЛАУ) в SMath Studio можно использовать различные методы. Для решения СЛАУ как с действительными, так и с комплексными коэффициентами можно использовать метод Крамера и метод обратной матрицы.
При расчете методом Крамера для нахождения определителей матриц
(детерминант) используют кнопку  с панели «Матрицы» или функцию det.
с панели «Матрицы» или функцию det.
37

При решении системы методом обратной матрицы составляют матрицу коэффициентов при неизвестных и вектор (матрицу-столбец) свободных членов. Пример решения СЛАУ методом обратной матрицы приведен на рисунке 1.31.
Рисунок 1.31 – Метод обратной матрицы
В примере 2, рисунок 1.31, показана эксклюзивная способность SMath Studio решать СЛАУ методом обратной матрицы сразу для нескольких вариантов правой части уравнений. Каждый вариант правой части записывается при расчете в отдельный столбец в матрице свободных членов.
Матрица результатов расчета будет содержать столько же столбцов.
И методом Крамера, и методом обратной матрицы можно решать системы уравнений в символьном виде. Такая возможность продемонстрирована в примере 3, рисунок 1.31. При символьных вычислениях для выведения результата расчета используют значок « → » (оператор символьного вычисления) с боковой панели «Арифметика».
Встроенная функция roots предназначена для решения систем нелинейных уравнений, но ее можно успешно использовать и для решения СЛАУ, таблица 1.7. Функция roots находит только действительные решения.
38
Таблица 1.7
roots(2) |
Нахождение корней системы уравнений. Возвращает |
|
roots(f(z);z) |
значения в векторе z, при которых функции вектора f(z) |
|
равны нулям. |
||
|
||
roots(3) |
Нахождение корней системы уравнений с учётом |
|
roots(f(z);z;z0) |
указанных приближений в векторе z0. Возвращает |
|
значения в векторе z, при которых функции вектора f(z) |
||
|
||
|
равны нулям. |
|
|
|
Как уравнения, так и переменные в roots задаются с помощью вектора
(матрицы-столбца). |
Уравнения |
можно |
задать |
непосредственно |
в |
первоначальном виде, где используют булево (жирное) равно. Можно также
предварительно привести уравнения к виду f(x)=0. Диапазон искомых корней
не зависит от предустановленного диапазона во вкладке <Сервис> <Опции>
<Вычисление>.
При решении системы нелинейных уравнений часто система имеет не
одно, а несколько возможных решений. Функция roots(2) выдаст только один
вариант решения. Для нахождения других вариантов решения целесообразно
использовать функцию roots(3), в которой задаются приближенные значения
неизвестных. Для системы с двумя неизвестными число решений и начальные
приближения можно определить графически, хотя это достаточно трудоемко.
Примеры решения систем уравнений функцией roots приведены на
рисунке 1.32.
39
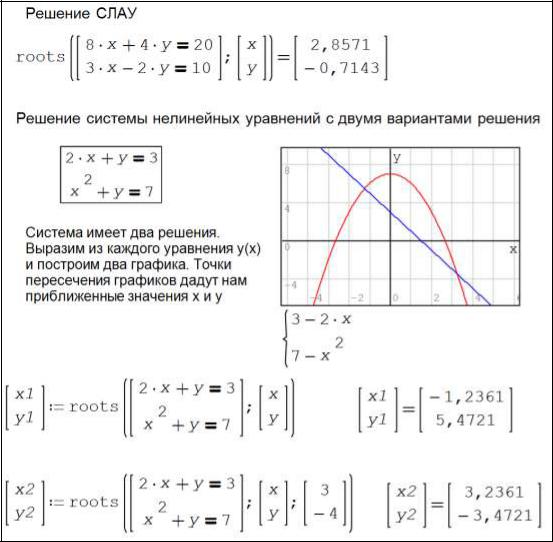
Рисунок 1.32 – Использование функции roots для решения систем уравнений
1.12 Символьные вычисления
Если используется символьная математика, то результатом вычисления будет выражение.
Выполнить символьное преобразование для выражения можно, если использовать символьный знак равенства  . В отличие от обычного знака равенства, символьный знак равенства способен возвращать выражения. Он вставляется либо с панели <Арифметика>, либо с клавиатуры комбинацией клавиш <Ctrl>+< . >.
. В отличие от обычного знака равенства, символьный знак равенства способен возвращать выражения. Он вставляется либо с панели <Арифметика>, либо с клавиатуры комбинацией клавиш <Ctrl>+< . >.
40
