Расчет электрических цепей в Smath Studio (учебное пособие)

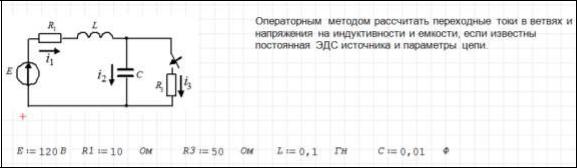
В SMath Studio оператора процедуры обратного преобразования Лапласа нет,

поэтому для перехода от изображений к оригиналам целесообразно использовать стандартный алгоритм используемой в электротехнике теоремы разложения. И здесь успешность расчета опять зависит от того, какие корни получатся в процессе расчета: действительные или комплексно-сопряженные.

При комплексных корнях возникают описанные выше неудобства при формировании полинома.

Кроме того, и при действительных, и при комплексных корнях в SMath Studio не получается сформировать читаемые результирующие выражения для оригиналов и их приходится формировать вручную, используя промежуточные результаты расчетов. Таким образом, расчет переходного процесса операторным методом целесообразно проводить в SMath Studio только для случая с действительными корнями. На рисунках 2.73 - 2.82 показан пример расчета переходного процесса в электрической цепи операторным методом для случая с действительными корнями характеристического уравнения.

Рисунок 2.73 – Исходные данные

Рисунки вставлены на рабочий лист из другого приложение через меню

Вставка, Рисунок.

На рисунке 2.74 записаны независимые начальные условия и представлена схема замещения. В системе уравнений на рисунке 2.75

используем знак <=> с панели инструментов Булева.

101

Рисунок 2.74 – Начальные условия и операторная схема замещения

Рисунок 2.75 – Система уравнений по законам Кирхгофа в операторной форме

102

Рисунок 2.76 – Операторные выражения для токов в ветвях и напряжений на реактивных элементах

Для получения результатов решения системы уравнений при символьных вычислениях используем знак < > с панели инструментов Арифметика,

рисунок 2.76. Далее, вручную присваиваем выражения для операторных токов на основе значений в полученной матрице результатов.

Далее в соответствии с алгоритмом операторного метода осуществляем переход от операторных изображений к оригиналам по теореме изображений.

Для всех токов и напряжений последовательность действий одинакова, поэтому на рисунках 2.77 – 2.79 представлены примеры только для тока через индуктивность и напряжения на емкости. Вручную разъединяем и присваиваем числитель и знаменатель операторного изображения как функции от р - N(p) и M(p). Приравниваем знаменатель к нулю и находим корни характеристического

103

уравнеия с помощью встроенной функции solve(4). Решение получим только,

если корни действительные.

Рисунок 2.77 – Применение теоремы разложения для получения оригинала тока через индуктивность

104

Для получения производной от знаменателя используем знак

производной с панели инструментов Функции.

Аналогичные действия проводим для получения оригинала напряжения на емкостном элементе.

Рисунок 2.78 – Применение теоремы разложения для получения оригинала напряжения на емкости

105

При комплексных корнях применение SMath Studio ограничено,

использовать его есть смысл только как калькулятор комплексных чисел и для получения операторных изображений. На рисунках 2.79 – 2.81 показан расчет операторных изображений токов для схемы, рассчитанной ранее классическим методом, рисунок 2.64.

Рисунок 2.79 – Система уравнений по законам Кирхгофа в операторной форме

На рисунке 2.80 все вычисления проведены в символьной форме, поэтому в качестве знака равно используется знак < > с панели инструментов

Арифметика. Комплексные корни можно определить только с помощью встроенной функции polyroots, работа с которой описана при рассмотреннии классического метода. Продолжение расчета и применения теоремы разложения для случая с комплекными корнями осуществляется вручную

106

Рисунок 2.80 – Операторные выражения для токов в ветвях и напряжения на индуктивности

Рисунок 2.81 – Определение корней характеристического уравнения

107

Переходной процесс в электрической цепи можно рассчитывать и численно. Для численного решения дифференциальных уравнений в SMath Studio можно применять дополнение <Mathcad Toolbox> из онлайн – галереи.

На верхней панеле инструментов находим вкладку <Дополнения>, откроется диалоговое окно, в котором открываем дополнительную вкладку <Локальное

хранилище>, из открывшегося списка устанавливаем <Mathcad Toolbox>. Это дополнение содержит функции rkfixed и Rkadapt. Обе функции используют для решения метод Рунге — Кутты четвертого порядка, rkfixed — с

фиксированным шагом, Rkadapt — с адаптивным шагом. На рисунках 2.82 - 2.83 показан расчета переходного процесса в сложной электрической цепи с двумя накопителями энергии с помощью функции rkfixed.

Рисунок 2.82 – Исходная система уравнений, составленная по законам Кирхгофа для мгновенных значений

108

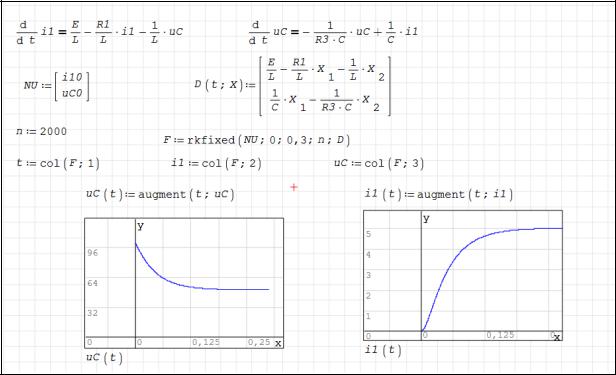
Рисунок 2.82 – Численное решение с помощью функции rkfixed

109

Список использованных источников

1 Приказ Минкомсвязи России «Об утверждении методических рекомендаций по переходу государственных компаний на преимущественное использование отечественного программного обеспечения, в том числе отечественного офисного программного обеспечения». – М.: Минцифры России, 2019. — URL: https://digital.gov.ru/ru/documents/6294 (дата обращения 08.11.2020)

2 Ушаков Ю. А., Ушакова Н. Ю. О специфике применения SMath Studio в

электротехнических расчетах // Современная наука: актуальные проблемы теории и практики. Серия: Естественные и Технические Науки. -2020. -№12. -

С. 145-155 DOI 10.37882/2223-2966.2020.12.38 3 SMath Studio Руководство пользователя.

– URL: https://www.smath.com/docs/SMathStudio_user_tutorial.pdf

4 Бессонов, Л. А. Теоретические основы электротехники. Электрические цепи:

учебник для бакалавров: учебник для студентов высших учебных заведений, обучающихся по направлениям подготовки дипломированных специалистов "Электротехника, электромеханика и электротехнологии", "Электроэнергетика", "Приборостроение" / Л. А. Бессонов.- 11-е изд., перераб. и доп. - Москва : Юрайт, 2013. - 702 с. - ISBN 978-5-9916-2562

5РГЗ №1 по дисциплине ТОЭ / составители Н.Ю.Ушакова, Л.В.Быковская; Оренбургский гос. ун-т. – Оренбург: ОГУ, 2023. – 50 с.

6РГЗ №2 по дисциплине ТОЭ / составители Н.Ю.Ушакова, Л.В.Быковская; Оренбургский гос. ун-т. – Оренбург: ОГУ, 2023. – 44 с.

7Семенова, Н. Г. Расчет и моделирование электрических и магнитных цепей [Электронный ресурс] : учебное пособие / Н. Г. Семенова, Н. Ю. Ушакова, Л. В. Быковская . - Оренбург : ОГУ. - 2021. - 186 с.

110