Расчет электрических цепей в Smath Studio (учебное пособие)

Рисунок 2.58 – Решение характеристического уравнения с действительными корнями

Для определения постоянных интегрирования определяем зависимые начальные условия для свободных составляющих, рисунок 2.59. Записываем систему уравнений по законам Кирхгофа для свободного режима и решаем ее с помощью встроенной функции roots. Решение систем линейных алгебраических уравнений (СЛАУ) в SMath Studio можно осуществить методом обратной матрицы или с использованием встроенной функции roots(f(x); x; c),

где первый параметр это функция, второй – аргумент, третий – начальное приближение. На рисунке 2.59 аргументами функции roots() являются вектор,

состоящий из уравнений системы и вектор неизвестных величин (i1sv0; i3sv0; uLsv0).

91

Рисунок 2.59 – Определение зависимых начальных условий

Рисунок 2.60 – Определение постоянных интегрирования

92

Рисунок 2.61 – Свободные составляющие искомых токов и напряжений

Рисунок 2.62 – Переходные токи и напряжения

93

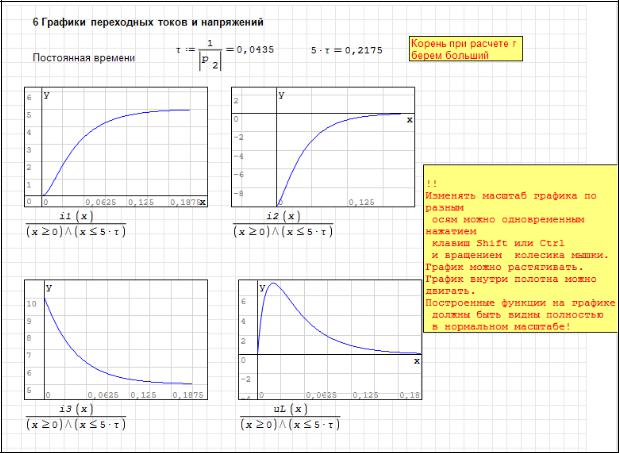
На рисунках 2.61, 2.62 записаны результаты расчета. Все выражения набираются с клавиатуры (вручную) на основе полученных выше результатов.

В последней строке на рисунке 2.62 проведена проверка полученных выражений для токов на основании уравнения, составленного для исходной электрической цепи, по первому закону Кирхгофа.

Завершается расчет простроением графических зависимостей искомых величин от времени, рисунок 2.63. По времени график ограничивают временем переходного процесса, то есть токи и напряжения должны достичь принужденных составляющих.

Рисунок 2.63 – Построение графиков переходных токов и напряжений

Рассмотрим второй пример расчета переходного процесса с комплексно-

сопряженными корнями характеристического уравнения.

94

Рисунок 2.64 – Запись системы уравнений

Рисунок 2.65 – Расчет принужденных составляющих

95

Рисунок 2.66 – Расчет независивых начальных условий

Рисунок 2.67 – Решение характеристического уравнения с комплексно-

сопряженными корнями

96

На рисунках 2.64 - 2.66 присутствуют простые вычисления в SMath Studio. Сложности возникают при решении характеристического уравнения, так как функция solve решает уравнения только с действительными корнями.

Единственно возможный путь решения уравнения с комплексными корнями на сегодняшний день в бесплатной версии SMath Studio - это использование встроенной функции polyroots. Функция предназначена для нахождения корней полинома, поэтому сначала нужно вручную преобразовать характеристическое уравнение до вида полинома. На рисунке 2.67 задаются коэффициенты квадратного уравнения Ау, Ву, Су. Дискриминант можно не находить. Вектор коэффициентов v записывается от свободного члена вниз в порядке возрастания степени неизвестного.

Рисунок 2.68 – Определение зависимых начальных условий

97

Определение зависимых начальных условий, рисунок 2.68, проводим аналогично случаю с действительными корнями. Для решения системы линейных уравнений применяем встроенную функцию roots.

Рисунок 2.69 – Определение постоянных интегрирования

Решение систем трансцендентных уравнений в SMath Studio функцией roots не дает результата, поэтому сначала преобразуем систему двух уравнений, используя метод подстановки, к одному уравнению. Затем решаем уравнение с помощью встроенной функции solve, причем в качестве неизвестного берем котангенс - ctg 1 или ctg 2. При попытке получить сразу

угол решение уравнения SMath Studio выдает в виде вектора с несколькими

98

корнями. Также SMath Studio выдает ошибку при решении системы, если свободные составляющие токов или напряжений, i1sv0 или uCsv0, равны нулю В таком случае решение продолжаем вручную, принимая =0.

Рисунок 2.70 – Свободные составляющие искомых величин

Рисунок 2.71 – Переходные токи и напряжения

99

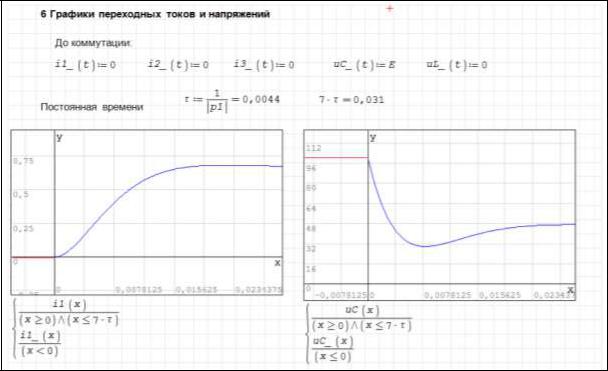
Исходя из результатов решения, формируются вручную выражения для свободных составляющих, рисунок 2.70, и для переходных токов и напряжений, рисунок 2.71.

На рисунке 2.72 показано построение графических зависимостей. На рисунке показано выполнение законов коммутации: ток через индуктивность и напряжение на емкости не могут изменяться скачком. На одном полотне строится два графика: ток через индуктивность до коммутации и после или напряжение на емкости до коммутации и после.

Рисунок 2.72 – Построение графических зависимостей

Операторный метод расчета переходных процессов заключается в том,

что при расчётах действительные функции времени f(t), описывающие процессы в электрических цепях и называемые оригиналами, заменяют их операторными изображениями F(p) с помощью преобразования (интеграла)

Лапласа. Электрическая схема заменяется операторной схемой замещения, из которой рассчитываются изображения искомых токов и напряжений, далее от изображений переходят к оригиналам.

100