Кластеризация

Обычно дана обучающая выборка (размеченные данные), по которым строится модель: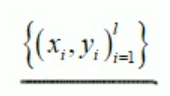

На практике встречается задача, когда исходный набор объектов x не размечен и нужно построить модель, которая разнесет образы по группам (классам), используя некую заданную метрику между объектами – это и есть задача кластеризации:

На выходе нужно найти:

Алгоритм кластеризации – отнесение каждого объекта X_i к тому или иному кластеру.

Так как этот алгоритм должен сам разнести объекты по классам – это обучение без учителя.

Для чего делать кластеризацию данных:

Возможные проблемы кластеризации:

Часто задача кластеризации не имеет четко выраженного единственного решения, например, множество точек можно разбить и на 2, и на 4 и на 6 кластеров.

В итоге для одних и тех же данных могут получаться разные результаты кластеризации:

Второй проблемой является то, что сами кластеры могут образовывать разные типы структур:

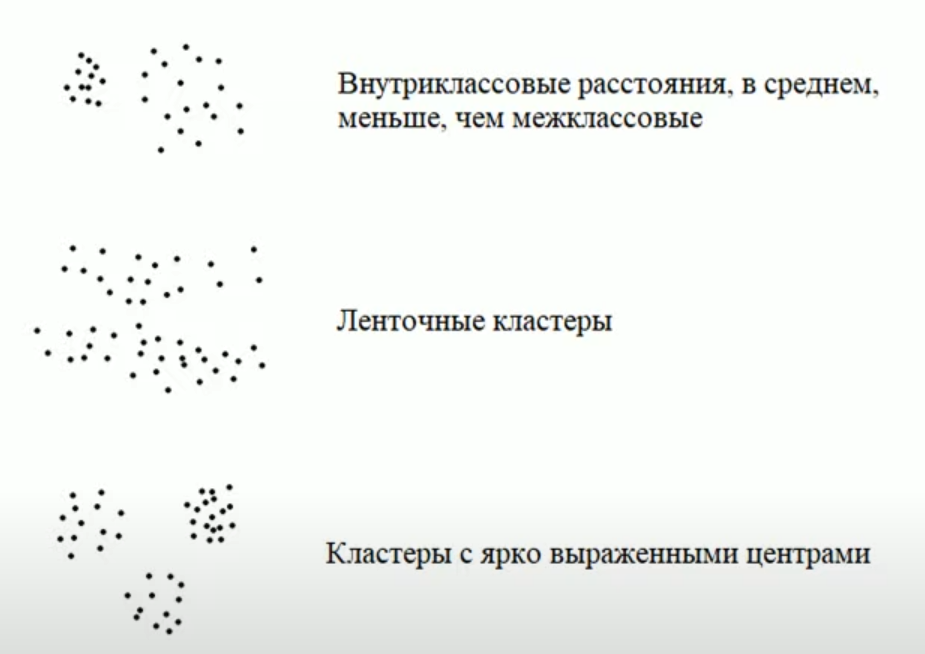
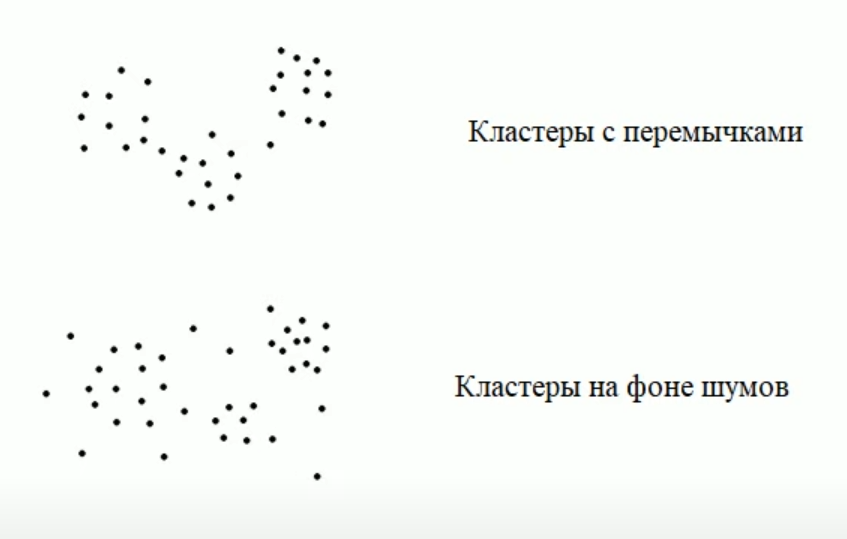
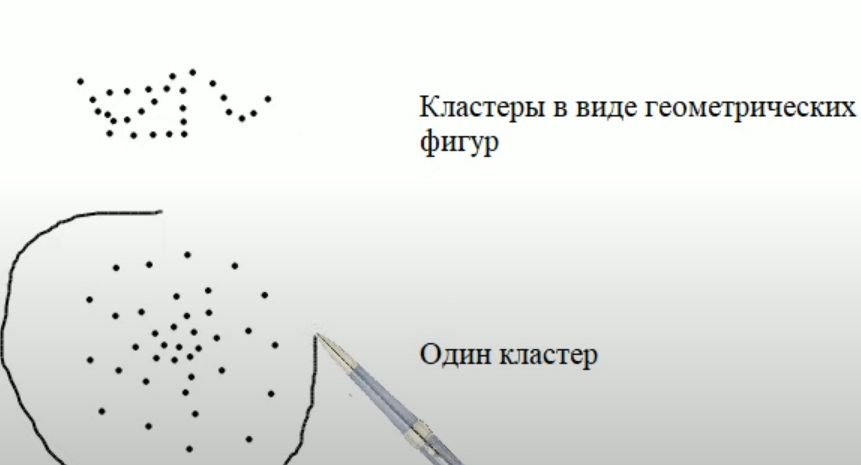
В последних двух примерах вообще нет четко выраженных отдельных кластеров, несмотря на то что в реальности различия могут быть. В таких случаях задачу следует решать другими методами.

Когда сформирована задача кластеризации следует сформулировать критерии для оценки качества разбиения образов по группам.

Мы будем исходить из того, что расстояние между объектами всегда можно определить, иначе задача кластеризации нерешаема. Также нужно чтобы была модель, которая относила бы образ X к тому или иному кластеру:

Исходя из этих данных можно выделить 2 очевидных критерия:

Первый:

В числителе выбираются все объекты, которые относятся с точки зрения модели к одному и тому же кластеру и делится на их количество

По аналогии:

Тут мы выбираем объекты из разных кластеров и делим на количество этих объектов.

Первая характеристика (F0) – должна быть минимальна, а вторая (F1) – максимальна.

Объединить эти два параметра можно так:

Если помимо расстояния мы можем определять и набор признаков для каждого объекта, то дополнительно можно ввести понятие центра кластера.

Тут мы берем и усредняем все признаки для всех объектов , которые относятся к каждому отдельному кластеру . Получаем множество центров для каждого кластера

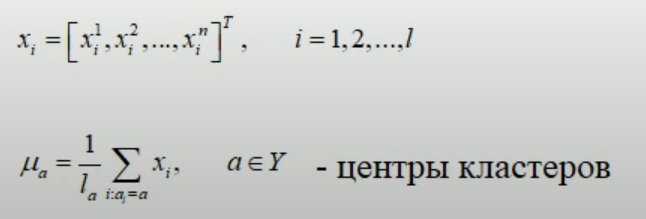
Уже относительно этих центров вычислять внутрикластерное и межкластерное расстояния проще (потому что используется всего одно число (то есть центры) и соответствующие образы . А межкластерное расстояние вычисляется просто как расстояние между центрами

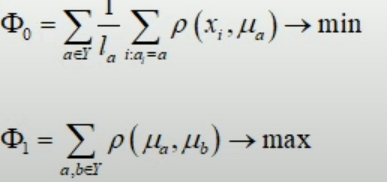
Далее эти характеристики объединяются очевидным образом:

Вопрос – что это за объекты, для которых можно вычислить только расстояние между ними, но не центры кластеров? Например, это могут быть расстояния между словами:

Мы можем сформулировать метрику, которая определяла бы близость этих слов, но представить каждое слово в виде набора признаков невозможно.

То же самое можно сделать и со звуками или порядком нуклиотидов в ДНК, есть много задач.

МЕТОД К-СРЕДНИХ (алгоритм Ллойда)

Пусть у нас есть набор объектов каждый из которых представлен в N-мерном числовом признаковом пространстве , т.е. каждый объект это ничто иное как числовой вектор (вектор, состоящий из определенных чисел)

Например, если число признаков у нас 2 (f1 и f2), то это просто множество точек:

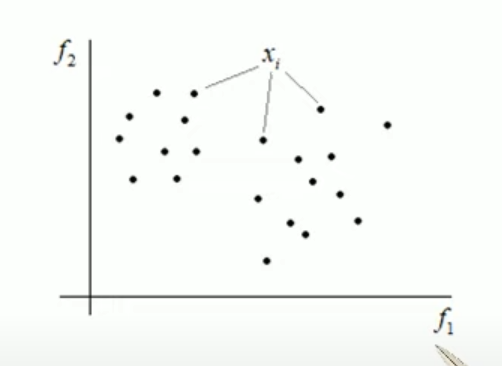
Наша задача разбить это множество объектов по кластерам, например, так:

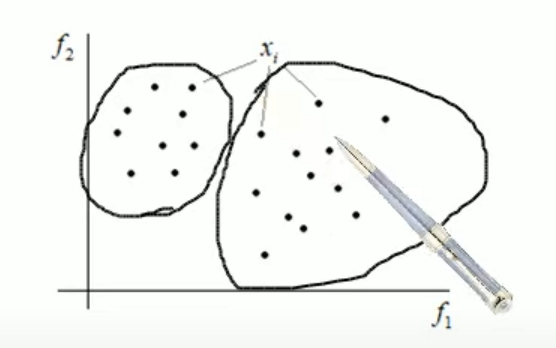
Для этого задается:

То есть мы заранее задаем на сколько кластеров разбиваем объекты выборки.

Также мы определяем метрику:

Часто используется Евклидово расстояние:

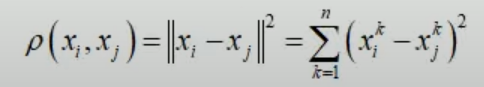
Далее для каждого кластера задаются начальные центры:

Это делается либо случайным образом, либо берутся любые k объектов и говорится, что это центры наших кластеров (все равно что выбрать несколько точек из рисунка с осями выше.

После этого запускается итерационный процесс (цикл):

В этом цикле каждая точка (если смотреть на тот же рисунок с осями) относится с ближайшим центром в соответствии с выбранной метрикой.

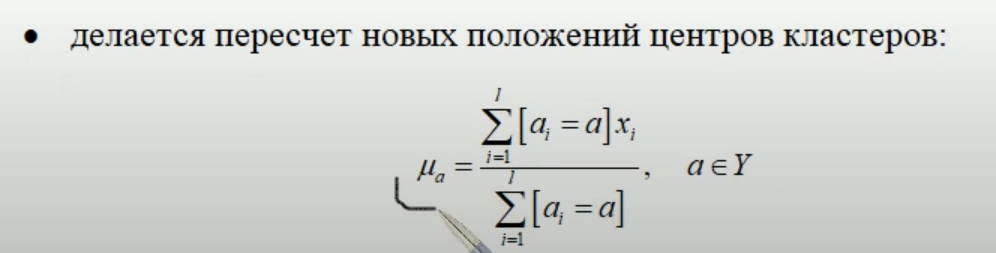
Тут мы суммируем все объекты, относящиеся к кластеру a и делим на их количество. Квадратная скобка, это нотация Айзерсена – выдает 1 если условие истинно и 0 в противном случае.

Цикл делается до тех пор, пока положения центров класетров не будут меняться меняются незначительно.