
2ЛР / lr2
.docxМИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
Московский технический университет связи и информатики
Лабораторная работа № 2
по дисциплине
“Системы искусственного интеллекта”
на тему
“АЛГОРИТМЫ МАШИННОГО ОБУЧЕНИЯ В СРЕДЕ MATLAB”
Выполнил: студент гр. БЗС2002
Ломакин А. А.
Проверила: Матюнина Д. Д.
Москва 2023
Цель работы
Сравнить работу алгоритмов машинного обучения и найти оптимальный из них для решения задачи классификации при самостоятельно сгенерированных начальных данных.
Исходные данные
Дан каталог, содержащий в себе численные характеристики различных моделей жилых помещений. Здания различаются по следующим параметрам (X — непосредственно характеристики, Y — вытекающие из них потребности, которые требуется прогнозировать):
• относительная компактность Х1;
• площадь поверхности Х2;
• площадь стен Х3;
• площадь крыши Х4;
• высота стен Х5;
• ориентация Х6;
• площадь остекления Х7;
• распределение площади остекления Х8;
• потребность в нагреве Y1; • потребность в охлаждении Y2;
В качестве начальных данных использованы данные интернет-источника: archive.ics.uci.edu/ml/datasets/Energy+efficiency. Входные данные доступны в средствах Exсel.
Код программы
Исходные данные были импортированы из Microsoft Excel в программу MATLAB. Ниже, в листинге 1, представлен код программы:
Листинг 1
%% Import data from text file % Script for importing data from the following text file: % % filename: C:\MatLab19\MyProjects\lab2SII.txt % % Auto-generated by MATLAB on 09-Oct-2023 10:11:45
%% Set up the Import Options and import the data opts = delimitedTextImportOptions("NumVariables", 12);
% Specify range and delimiter opts.DataLines = [1, Inf]; opts.Delimiter = "\t";
% Specify column names and types opts.VariableNames = ["X1", "X2", "X3", "X4", "X5", "X6", "X7", "X8", "Y1", "Y2", "Y1_R", "Y2_R"]; opts.VariableTypes = ["double", "double", "double", "double", "double", "double", "double", "double", "double", "double", "double", "double"];
% Specify file level properties opts.ExtraColumnsRule = "ignore"; opts.EmptyLineRule = "read";
% Specify variable properties opts = setvaropts(opts, ["X1", "X2", "X3", "X4", "X5", "X6", "X7", "X8", "Y1", "Y2", "Y1_R", "Y2_R"], "DecimalSeparator", ","); opts = setvaropts(opts, ["X1", "X2", "X3", "X4", "X5", "X6", "X7", "X8", "Y1", "Y2", "Y1_R", "Y2_R"], "ThousandsSeparator", ".");
% Import the data lab2SII1 = readtable("C:\MatLab19\MyProjects\lab2SII.txt", opts);
%% Clear temporary variables clear opts
%% Наивный байесовский классификатор Y1=lab2SII1.Y1_R; Y2=lab2SII1.Y2_R; u=length(unique(Y1)); disp(['There are', num2str(u),'unique output categories']);
c2=cvpartition(Y1, 'holdout'); X=[lab2SII1.X1, lab2SII1.X2, lab2SII1.X3, lab2SII1.X4, lab2SII1.X5, lab2SII1.X6, lab2SII1.X7, lab2SII1.X8]; Xtrain=X(training(c2,1),:); Xtest=X(test(c2,1),:); Ytrain=Y1(training(c2,1),:); Ytest=Y1(test(c2,1),:);
baymodel = fitcnb (Xtrain, Ytrain, 'Distribution', 'kernel'); Ypredict = predict(baymodel, Xtest) pernb_0 = 100* (1- (sum (Ytest~=Ypredict) /length (Ytest))); pernb_1 = 100* (sum(abs (Ytest - Ypredict) <=1)) /length (Ytest); disp(['Naive Bayes % within 1 unit - ', num2str(pernb_1), '8']);
[C, order] = confusionmat (Ytest, Ypredict); C_perc = diag(sum(C, 2))\C; figure; imagesc (C_perc); colorbar; xlabel ('Outputs'); ylabel ('Outputs'); title (['How many responses were correctly predicted within 1: ', num2str(pernb_1), '%']);
%% Регрессионные деревья model = TreeBagger (20, Xtrain, Ytrain, 'Method', 'Classification'); view (model. Trees{1}, 'mode', 'graph'); Ypredict2 = str2double ((predict (model, Xtest))); pernt_0 = 100* (1- (sum (Ytest~=Ypredict2)/length (Ytest))); pernt_1 = 100* (sum (abs (Ytest - Ypredict2) <=1)) /length (Ytest); disp(['Tree Bagger % within 1 unit - ', num2str(pernt_1), '%']);
%% Нейронные сети u = unique (Y1); Ytrain2 = zeros(length(Ytrain), length (u)); for i = 1: length (u) a = Ytrain == u(i); Ytrain2 (:, i) = double (a); end
net = patternnet (10); %% Обучение на 10 нейронах net = train(net, Xtrain', Ytrain2'); Y3 = net (Xtest')'; for i = 1: length (Y3) [~,m] = max(Y3(i, :)); Ypredict3(i, :) = u(m); end pernn_0 = 100* (1- (sum (Ytest ~=Ypredict3)/length(Ytest))); pernn_1 = 100* (sum(abs (Ytest - Ypredict3) <=1))/length(Ytest); disp(['Neural Networks % within unit 1 - ', num2str(pernn_1), '%'])
[C, order] = confusionmat(Ytest, Ypredict3); C_perc = diag(sum(C, 2)) \ C; figure(2); imagesc(C_perc); colorbar; xlabel('Outputs'); ylabel('Outputs'); title(['How many responses were correctly predicted within 1 - ' num2str(pernn_1), ' %']); |
Ниже приведены графики, иллюстрирующие результаты работы программы:
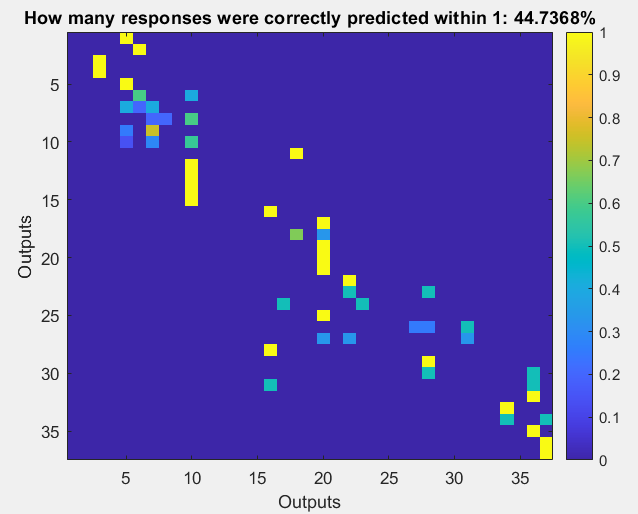
Рисунок 1 – Доля правильно предсказанных ответов с использованием наивного Байсесовского алгоритма
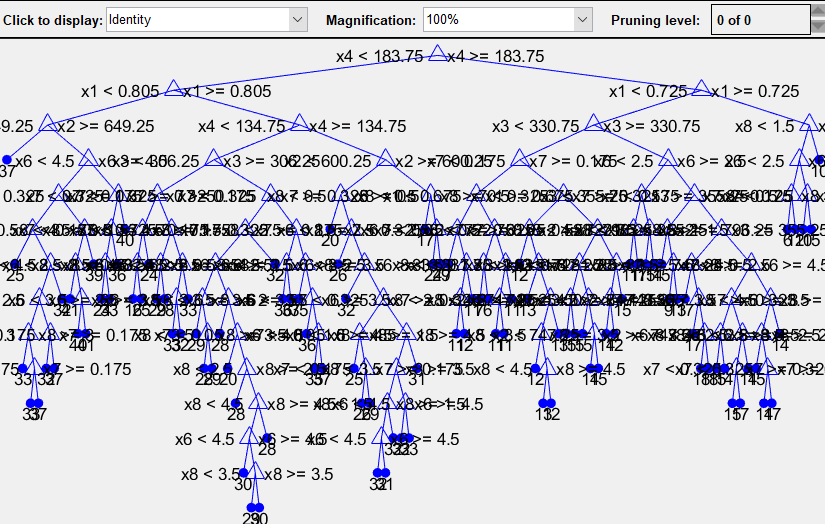
Рисунок 2 – Дерево распределения
![]()
Рисунок 3 – Доля правильно предсказанных ответов с использованием регрессионных деревьев
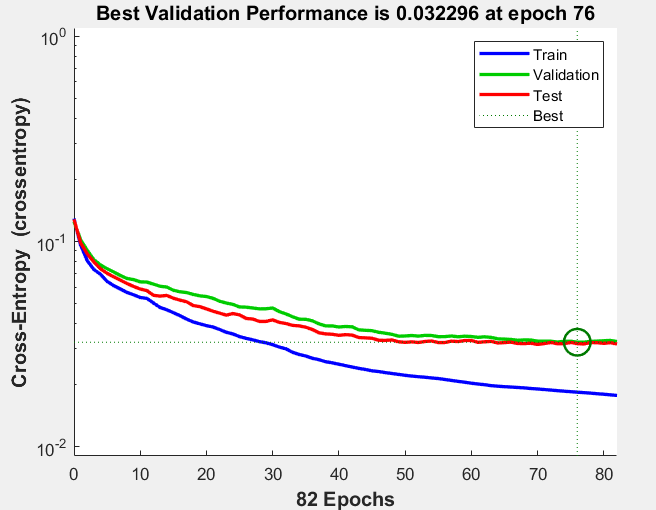
Рисунок 4 – График качества обучения трех различных выборок с использованием 10 нейронов
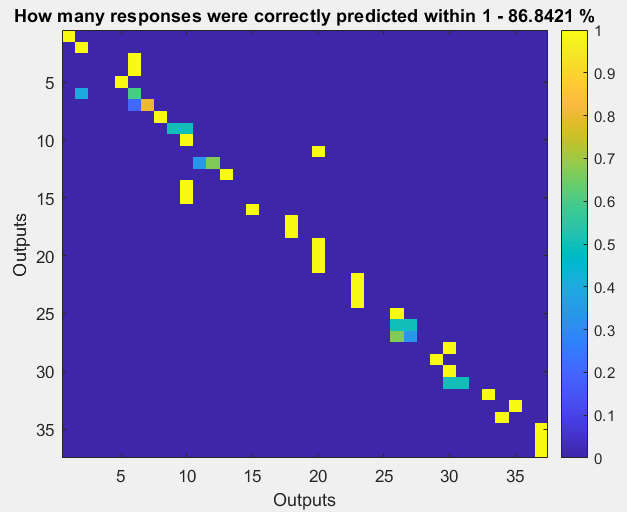
Рисунок 5 – Доля правильно предсказанных ответов с использованием обучения нейросети при 10 нейронах
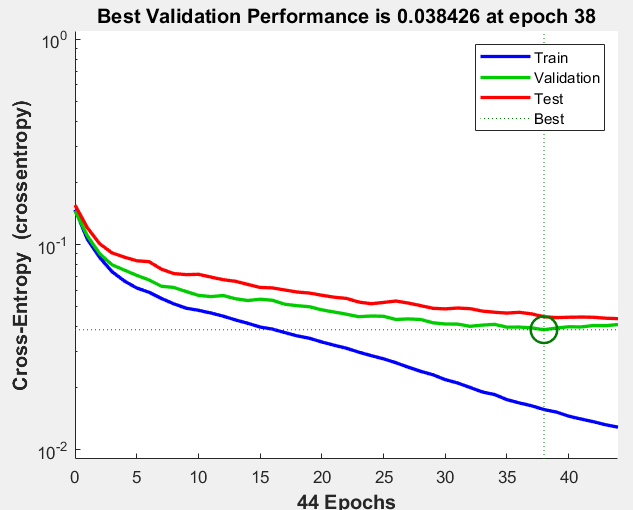
Рисунок 6 – График качества обучения трех различных выборок с использованием 30 нейронов
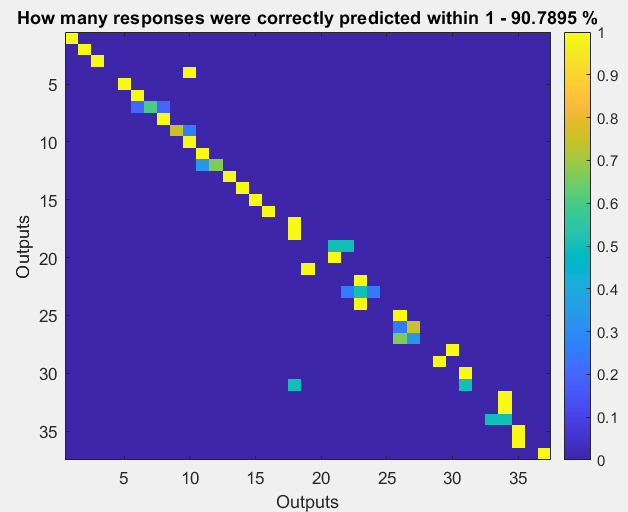
Рисунок 7 – Доля правильно предсказанных ответов с использованием обучения нейросети при 30 нейронах
Выводы
В ходе лабораторной работы была рассмотрена задача классификации – рассматривалась потребность зданий в нагреве и охлаждении. Использовались такие алгоритмы классификации, как наивный байесовский классификатор, регрессионные деревья и нейронные сети. Для разных алгоритмов классификации получились разные доли правильно предсказанных ответов: для наивного байесовского классификатора – 44.74%, для регрессионных деревьев – 94.74%, для нейронных сетей – 86.84% (при 10 нейронах) и 90.79% (при 30 нейронах). Можно сделать вывод, что алгоритм регрессионных деревьев показал лучший результат.
