Практика / PR_LR

Федеральное агентство связи

Государственное образовательное учреждение высшего профессионального образования

Московский Технический Университет Связи и Информатики

(МТУСИ)

Кафедра технической электродинамики и антенн

ПРАКТИЧЕСКОЕ ЗАДАНИЕ

по дисциплине

ЛИНИИ РАДИОСВЯЗИ И МЕТОДЫ ИХ ЗАЩИТЫ

Выполнил:

студент группы БЗС2002

Ломакин А. А.

Проверил:

Смирнов Е. В.

1. Цель работы

1. Изучение методов расчета радиополя в условиях городской застройки.

2. Освоение метода равномерной геометрической теории дифракции.

3. Исследование характера изменения поля в условиях городской застройки в зависимости от условий задания.

2. Исходные данные

Таблица 1 – исходные данные

N варианта	Объект изучения	Тип стены здания	Частота излучения, МГц	Поляризация
12	S2	железобетонная	1800	перпендикулярная

Диэлектрическая проницаемость бетона:

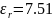
Удельная проводимость бетона:

Шаг: 0.033 м, т. к. λ = c/f = 300/1800 = 16.6 см => Δ = 16.6/5 = 3.3 см)

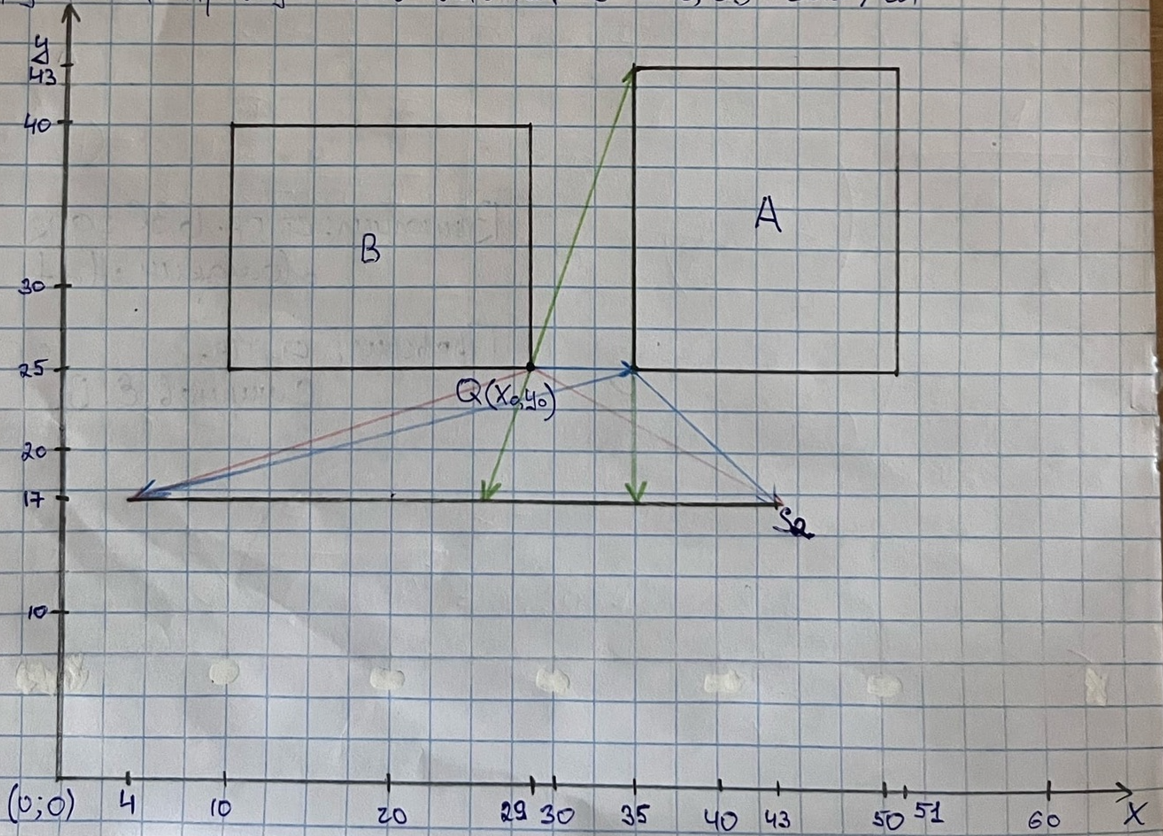
Рисунок 1 – зоны действия лучей

3. Зоны действия лучей

1. Прямые лучи:

2. Отражённые лучи: нет

3. Первая зона дифракции:

4. Вторая зона дифракции: => точка пересечения:

4. Расчёт E_fs

Найдём каждую точку с заданным шагом на пути S2:

Рисунок 2 – точки на пути S2

Найдём длину падающего в каждую точку луча:

Рисунок 3 – длина падающего луча

Найдём Efs в каждой точке:

Рисунок 4 – Efs в каждой точке

Так как Efs – комплексная величина, следует взять от неё модуль и построить график зависимости модуля Efs от координаты:

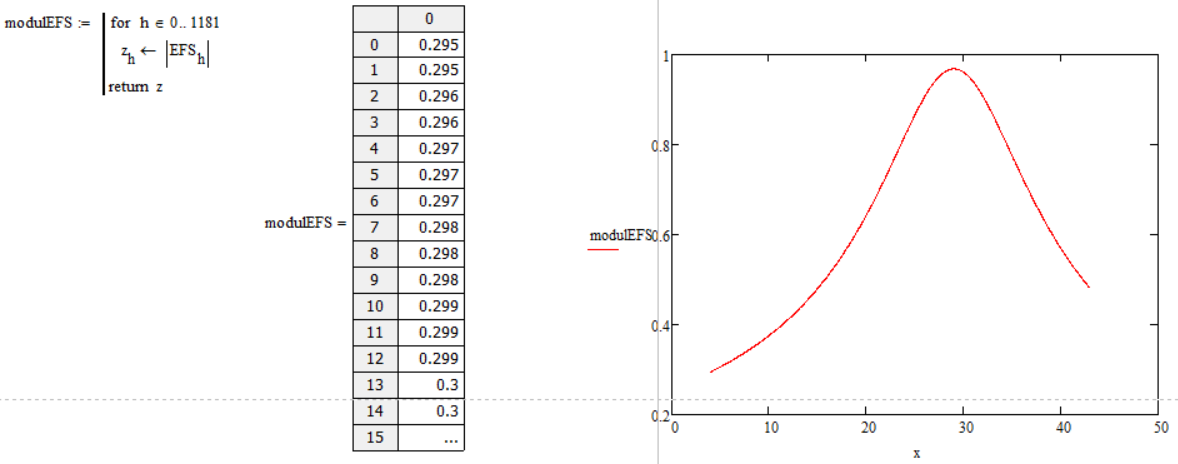
Рисунок 5 – модуль Efs и график модуля от координаты

5. Расчёт E_диф в первой зоне дифракции

Для начала следует найти угол для каждой точки на пути S2:

Рисунок 6 – угол

Затем найдём коэффициент дифракции в каждой точке:

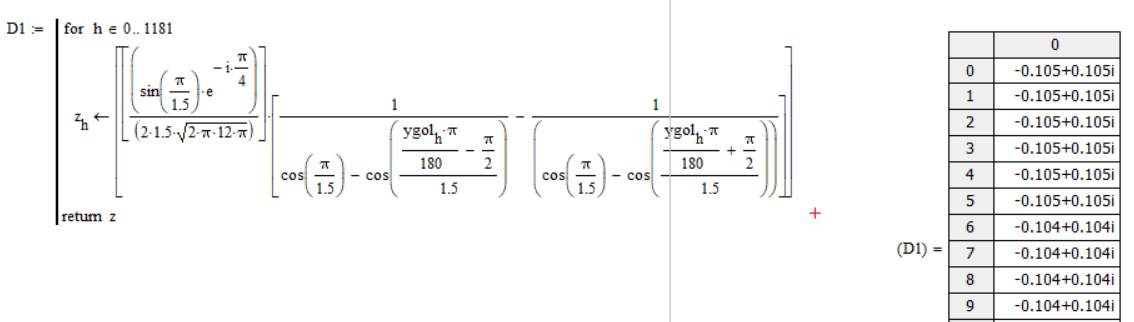
Рисунок 7 – коэффициент дифракции

Найдём длину дифрагированного луча для каждой точки:

Рисунок 8 – длина дифрагированного луча

Наконец, найдём E_диф в каждой точке:

Рисунок 9 – E_диф в каждой точке

Так как E_диф – комплексная величина, следует взять от неё модуль и построить график зависимости модуля E_диф от координаты:

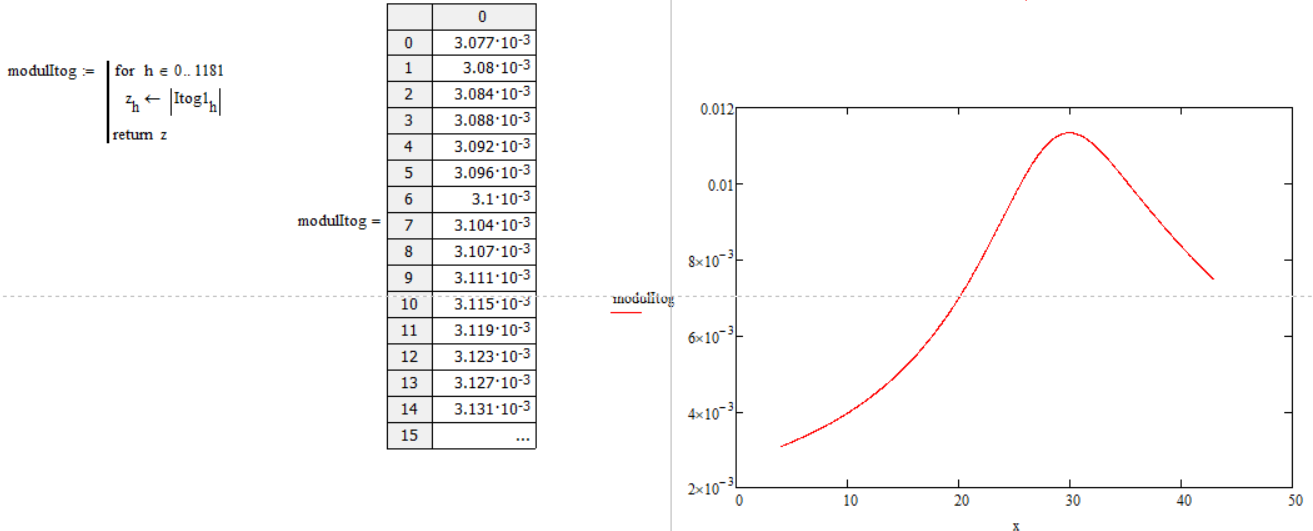
Рисунок 10 - модуль E_диф и график модуля от координаты

6. Расчёт E_диф во второй зоне дифракции

Произведя расчёты, аналогичные расчётам из пункта 5, получим следующие значения E_диф во второй зоне дифракции:

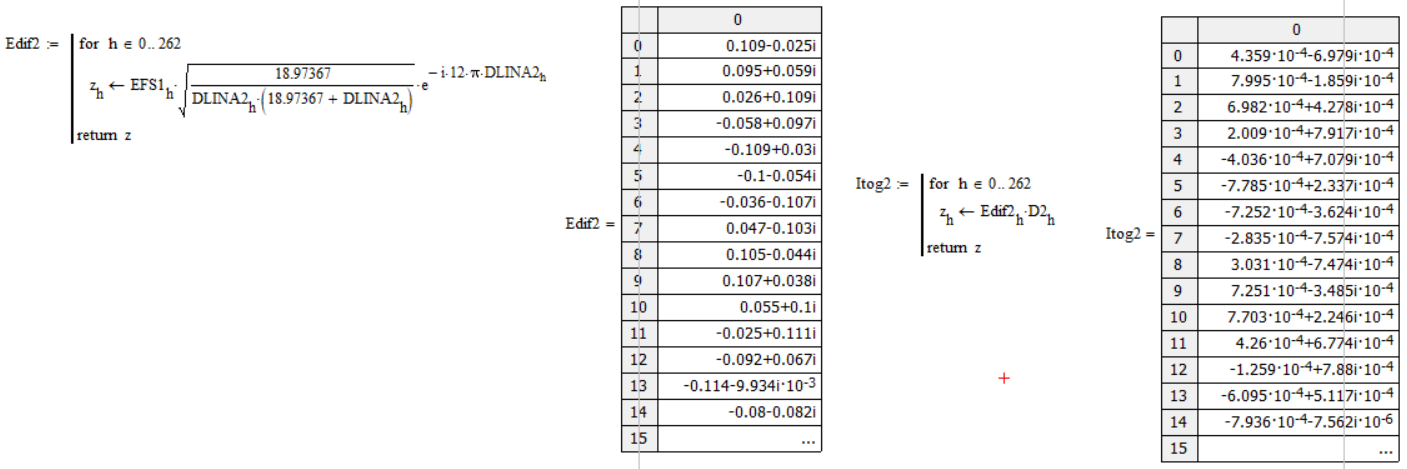
Рисунок 11 - E_диф в каждой точке

Так как E_диф – комплексная величина, следует взять от неё модуль и построить график зависимости модуля E_диф от координаты:

Рисунок 12 - модуль E_диф и график модуля от координаты

7. Сумма лучей

Найдём сумму всех падающих лучей (E_fs + E_диф в первой зоне дифракции + E_диф во второй зоне дифракции):

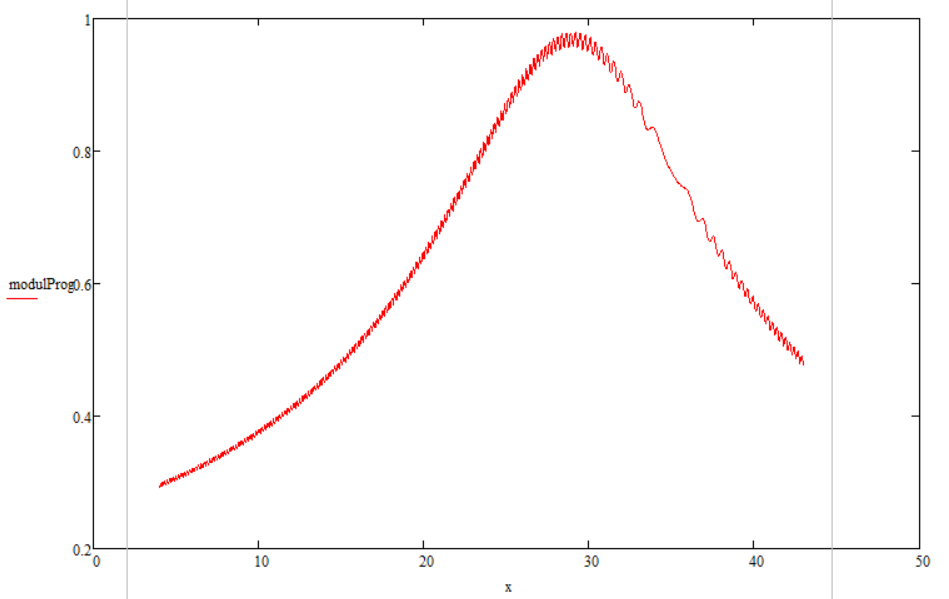
Рисунок 13 – сумма лучей на отрезке S2

8. Выводы

В ходе практического задания был произведен расчёт падающих от источника лучей в условиях городской застройки с применением ГТД. Были получены численные значения E_fs и E_диф в нескольких зонах. Результаты вычислений совпадают с эталонными значениями, что свидетельствует о корректном выполнении поставленной задачи.

Москва 2023