
Курсовая / Kyrsovaia
.docxМИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ордена Трудового Красного Знамени федеральное государственное
бюджетное образовательное учреждение высшего образования
МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
СВЯЗИ И ИНФОРМАТИКИ
Кафедра Многоканальные телекоммуникационные системы
Курсовая работа
Выполнил: студент группы БЗС2002
Ломакин А. А.
Проверил: Мирошниченко А.В.
1. Исходные данные
На рисунке 1 показано задание на проектирование КИХ-фильтра 80 порядка:

Рисунок 1 – АЧХ и ФЧХ заданного КИХ-фильтра
2. Расчёт КИХ-фильтра
Для начала следует аппроксимировать АЧХ и ФЧХ. В заданном варианте АЧХ есть 3 отрезка, два из которых являются прямыми, а один – эллипсом. Найдем уравнения данных прямых:
От 0 до 1200 Гц:
Уравнение прямой:
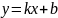


От 1200 до 2800 Гц:
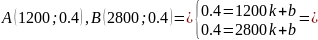

От 2800 до 4000 Гц:
Уравнение эллипса:

Центр эллипса О (2800; 1), a = 1200, b = 0.6;

В заданном ФЧХ 2 прямых, найдем их уравнения:
От 0 до 2800 Гц:
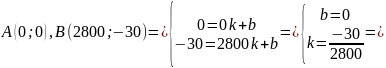
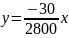
От 2800 до 4000 Гц:
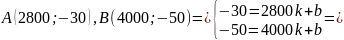

Таблица 1 – Аппроксимация АЧХ и ФЧХ
n |
f |
𝐾(f) |
𝜑(f) |
0 |
0 |
0 |
0 |
1 |
100 |
0.033 |
-3.36599 |
2 |
200 |
0.066 |
-6.73198 |
3 |
300 |
0.1 |
-10.0979 |
4 |
400 |
0.133 |
-13.4639 |
5 |
500 |
0.166 |
-16.8299 |
6 |
600 |
0.2 |
-20.1959 |
7 |
700 |
0.233 |
-23.5619 |
8 |
800 |
0.266 |
-26.9279 |
9 |
900 |
0.3 |
-30.2939 |
10 |
1000 |
0.33 |
-33.6599 |
11 |
1100 |
0.366 |
-37.0259 |
12 |
1200 |
0.4 |
-40.3919 |
13 |
1300 |
0.4 |
-43.7579 |
14 |
1400 |
0.4 |
-47.1239 |
15 |
1500 |
0.4 |
-50.4899 |
16 |
1600 |
0.4 |
-53.8559 |
17 |
1700 |
0.4 |
-57.2219 |
18 |
1800 |
0.4 |
-60.5879 |
19 |
1900 |
0.4 |
-63.9539 |
20 |
2000 |
0.4 |
-67.3198 |
21 |
2100 |
0.4 |
-70.6858 |
22 |
2200 |
0.4 |
-74.0518 |
23 |
2300 |
0.4 |
-77.4178 |
24 |
2400 |
0.4 |
-80.7838 |
25 |
2500 |
0.4 |
-84.1498 |
26 |
2600 |
0.4 |
-87.5158 |
27 |
2700 |
0.4 |
-90.8818 |
28 |
2800 |
0.4 |
-94.2478 |
29 |
2900 |
0.402087 |
-99.4838 |
30 |
3000 |
0.408392 |
-104.7198 |
31 |
3100 |
0.419052 |
-109.9557 |
32 |
3200 |
0.434315 |
-115.1917 |
33 |
3300 |
0.454564 |
-120.4277 |
34 |
3400 |
0.480385 |
-125.6637 |
35 |
3500 |
0.51266 |
-130.8997 |
36 |
3600 |
0.552786 |
-136.1357 |
37 |
3700 |
0.603137 |
-141.3717 |
38 |
3800 |
0.668338 |
-146.6077 |
39 |
3900 |
0.760208 |
-151.8436 |
40 |
4000 |
1 |
-157.0796 |
Построим АЧХ и ФЧХ в SciLab:
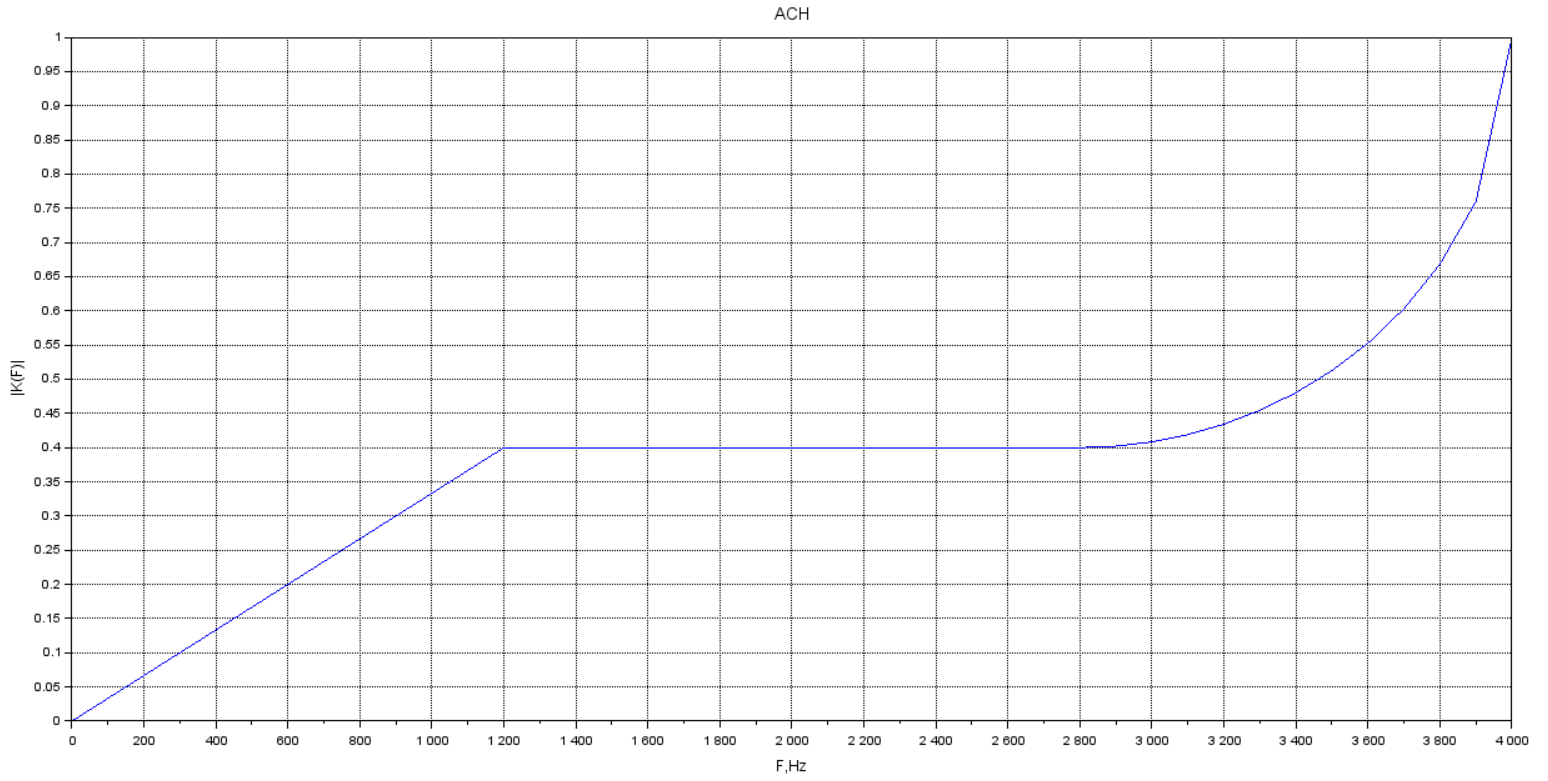
Рисунок 2 - АЧХ

Рисунок 3 – ФЧХ
Теперь постоим график действительной и мнимой части от АЧХ и ФЧХ, использовав формулу:
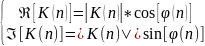 ,
,
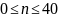
В таблице 2 представлены значения действительной и мнимой частей.
Таблица 2 - Значения мнимой и действительной частей АЧХ и ФЧХ
n |
f |
𝑅𝑒[𝐾(f)] |
𝐼𝑚[𝐾(f)] |
0 |
0 |
0 |
0 |
1 |
100 |
-0.03217 |
0.00734312 |
2 |
200 |
0.05946 |
-0.0286361 |
3 |
300 |
-0.07819 |
0.062343 |
4 |
400 |
0.08293 |
-0.103978 |
5 |
500 |
-0.07203 |
0.149556 |
6 |
600 |
0.04451 |
-0.194983 |
7 |
700 |
-1.04621*10-5 |
0.233 |
8 |
800 |
-0.05918 |
-0.259333 |
9 |
900 |
0.130157 |
0.270294 |
10 |
1000 |
-0.20575 |
-0.258009 |
11 |
1100 |
0.28615 |
0.228201 |
12 |
1200 |
-0.36039 |
-0.173555 |
13 |
1300 |
0.38997 |
0.0890075 |
14 |
1400 |
-0.4 |
-4.07846*10-6 |
15 |
1500 |
0.38997 |
-0.0890154 |
16 |
1600 |
-0.36038 |
0.173563 |
17 |
1700 |
0.31272 |
-0.249406 |
18 |
1800 |
-0.24938 |
0.312743 |
19 |
1900 |
0.17354 |
-0.360396 |
20 |
2000 |
-0.08903 |
0.389967 |
21 |
2100 |
1.38823*10-5 |
-0.4 |
22 |
2200 |
0.08899 |
0.389974 |
23 |
2300 |
-0.17355 |
-0.360391 |
24 |
2400 |
0.24939 |
0.312735 |
25 |
2500 |
-0.31273 |
-0.249397 |
26 |
2600 |
0.36039 |
0.173552 |
27 |
2700 |
-0.38997 |
-0.0890035 |
28 |
2800 |
0.4 |
-8.15692*10-6 |
29 |
2900 |
0.20106 |
0.348211 |
30 |
3000 |
-0.20418 |
0.353687 |
31 |
3100 |
-0.41905 |
-1.79671*10-5 |
32 |
3200 |
-0.217146 |
-0.376134 |
33 |
3300 |
0.22729 |
-0.39366 |
34 |
3400 |
0.48039 |
2.95129*10-6 |
35 |
3500 |
0.25633 |
0.443975 |
36 |
3600 |
-0.27638 |
0.478732 |
37 |
3700 |
-0.60314 |
1.8449*10-5 |
38 |
3800 |
-0.33419 |
-0.578783 |
39 |
3900 |
0.38013 |
-0.658342 |
40 |
4000 |
1 |
3.26795*10-5 |
Построим с помощью математического пакета Scilab график реальной части комплексного коэффициента передачи по полученным ранее точкам, а также график мнимой части КЧХ в диапазоне от 0 до Fд/2 (4000 Гц):

Рисунок 4 - Действительная часть КЧХ в диапазоне 0 ≤ 𝑓 < 𝐹д/2
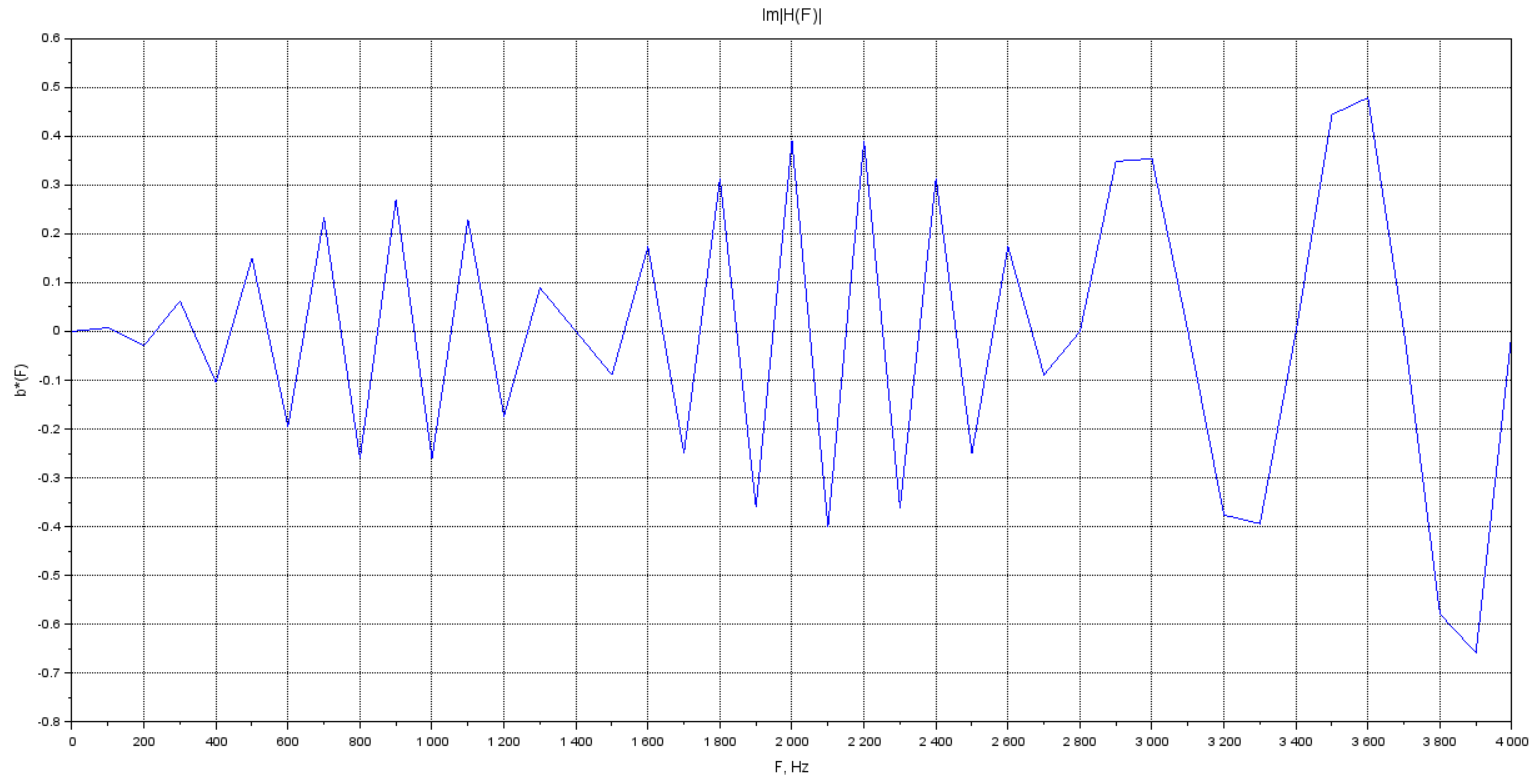
Рисунок 5 - Мнимая часть КЧХ в диапазоне 0 ≤ 𝑓 < 𝐹д/2
Достроим функцию согласно правилу:
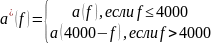


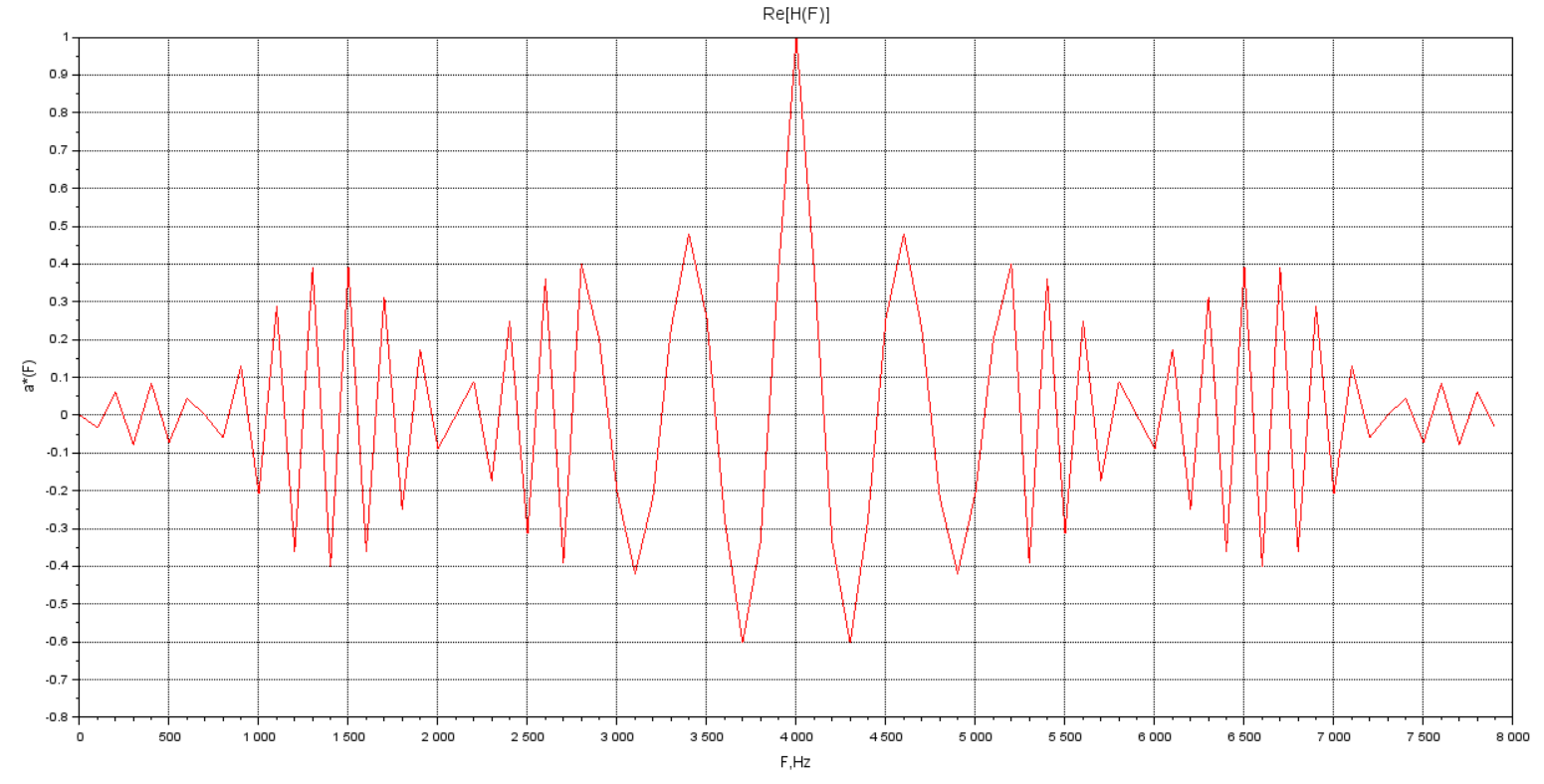
Рисунок 6 - Действительная часть в диапазоне 0 ≤ 𝑓 < 𝐹д
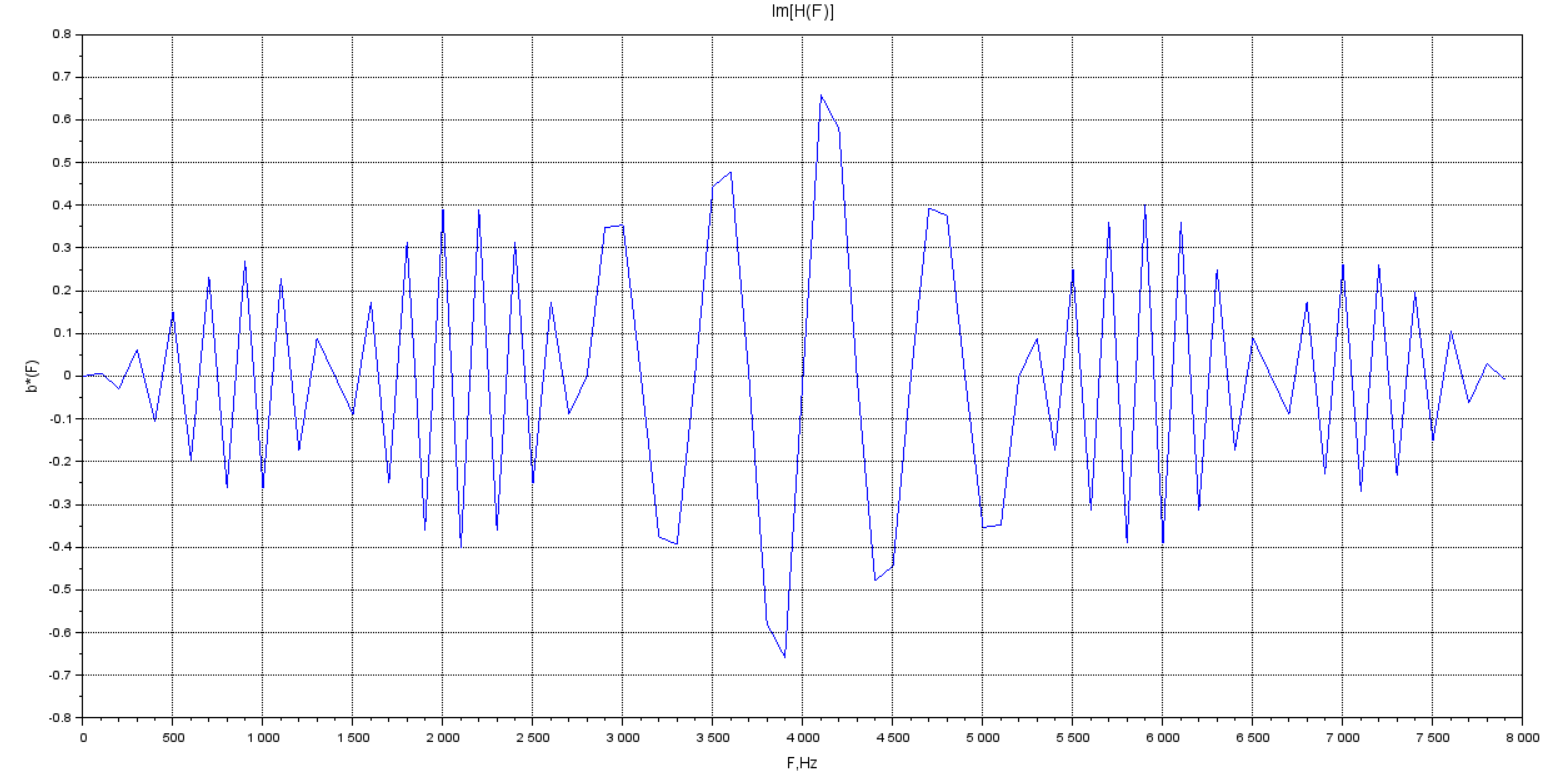
Рисунок 7 - Мнимая часть в диапазоне 0 ≤ 𝑓 < 𝐹д
Получим импульсную характеристику через обратное преобразование Фурье:

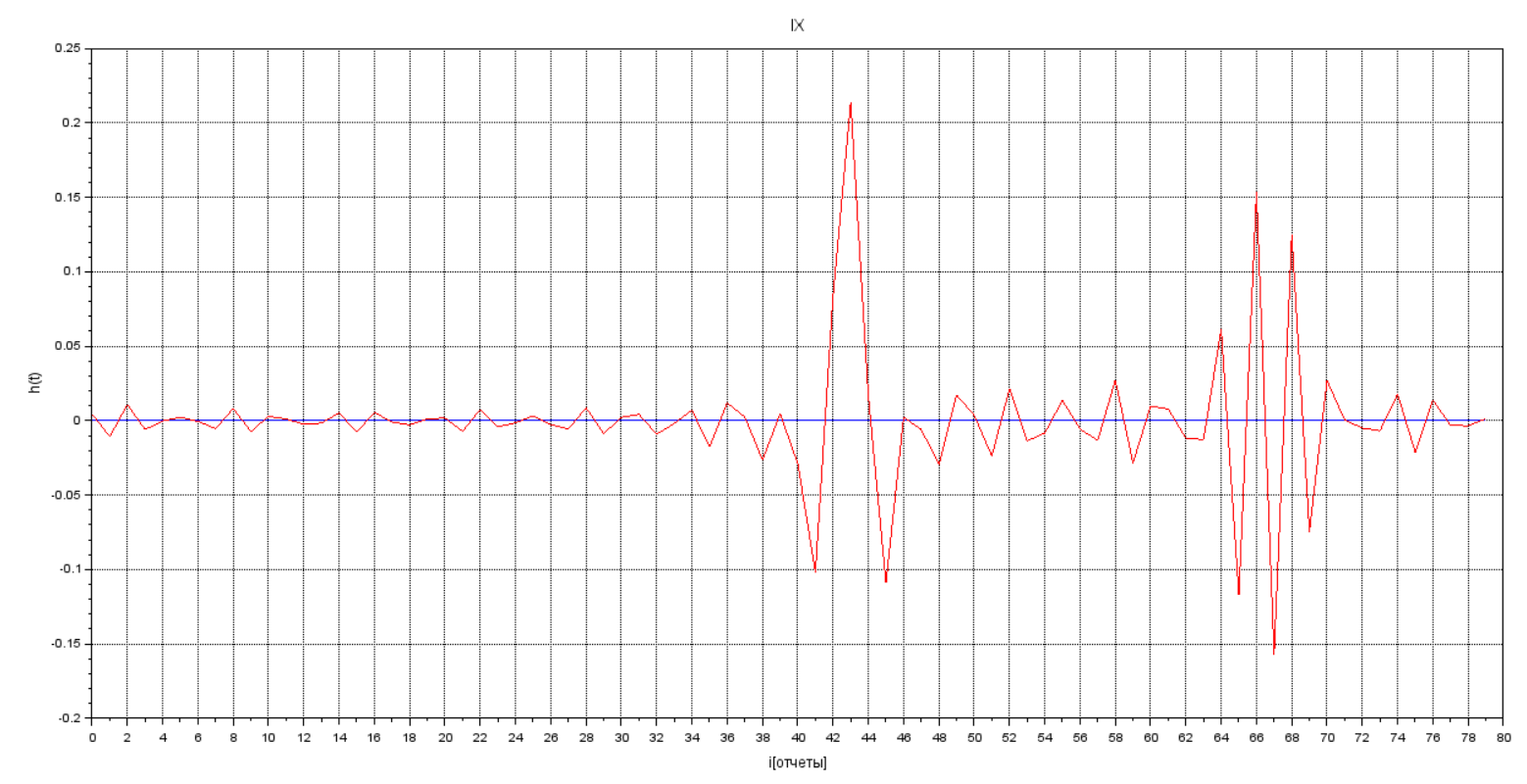
Рисунок 8 - Импульсная характеристика фильтра
3. Код SciLab
//Синтез АЧХ и ФЧХ по исходным данным
function ach=K(F)
if F>=0 & F<=1200 then
ach=(0.4./1200).*F
elseif F>1200 & F<=2800 then
ach=0.4
elseif F>2800 & F<=4000 then
ach=-sqrt((1-((F-2800).^2)./1200.^2).*0.6.^2)+1
end
endfunction
function fch=fi(F)
if F>=0 & F<=2800 then
fch = -(30./2800).*F*%pi
elseif F>=2800 & F<=4000 then
fch =((-F./60)+(50./3))*%pi
end
endfunction
//Построение графиков АЧХ и ФЧХ
ACH = zeros(1:41)
F = 0 : 100 : 4000
for i = 1:41
ACH(i,:) = K(F(i))
end
FCH = zeros(1:41)
F = 0 : 100 : 4000
for i = 1:41
FCH(i,:) = fi(F(i))
end
scf(0)
xgrid()
xtitle('ACH','F,Hz','|K(F)|')
plot(F,ACH)
scf(1)
xgrid()
xtitle('FCH','F,Hz','fi(F)')
plot(F,FCH)
//Нахождение действительной и мнимой части ДО расширения АЧХ и ФЧХ
REAL = abs(ACH).*cos(FCH)
NEREAL = abs(ACH).*sin(FCH)
scf(2)
xtitle('Re|H(F)|','F, Hz','a*(F)')
xgrid()
plot(F,REAL,'r')
scf(3)
xtitle('Im|H(F)|','F, Hz','b*(F)')
xgrid()
plot(F,NEREAL,'b')
//Нахождение действительной и мнимой части ПОСЛЕ расширения АЧХ и ФЧХ, а также нахождения КЧХ для реализации ИХ
Re = zeros(1:80)
Im = zeros(1:80)
Hfunc = zeros(1:80)
for i = 1:41
Re(i) = abs(ACH(i))*cos(FCH(i))
Im(i) = abs(ACH(i))*sin(FCH(i))
Hfunc(i)=Re(i)+%i*Im(i)
if i >= 2 then Hfunc(82-i) = Re(i)-%i*Im(i)
end
if i <> 1 then
Re(82-i) = Re(i)
Im(82-i) = -Im(i)
end
end
//Построение графиков Re и Im
F = 0:100:7900
scf(4)
xgrid()
xtitle('Re[H(F)]','F,Hz','a*(F)')
plot(F,Re,'r')
scf(5)
xgrid()
xtitle('Im[H(F)]','F,Hz','b*(F)')
plot(F,Im)
//Обратное преобразоввание Фурье
IX = ifft(Hfunc)
scf(6)
xgrid()
xtitle('IX','i[отчеты]','h(t)')
plot([0:79],imag(IX))
plot([0:79],real(IX),'r')
4. Разработка программы на языке ассемблера процессора ADSP-2181
.section/dm vars;
.var/circ coef[80] = 143,-352,353,-195,-5,75,-17,-175,267,-241,94,39,-83,-52,170,-254,180,-32,-92,40,57,-236,247,-135,-47,105,-86,-180,284,-286,73,136,-300,-62,229,-580,391,76,-865,150,-948,-3335,2750,7006,534,-3571,77,-196,-967,564,116,-776,701,-447,-272,446,-183,-438,892,-929,322,254,-389,-415,2010,-3837,5017,-5151,4087,-2437,880,14,-162,-224,584,
-692,453,-106,-113,45;
.var/circ simples[80] = 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0;
.section/pm program;
jump main; rti; rti; rti; rti; rti; rti; rti; rti; rti; rti; rti; rti; rti; rti; rti; rti; rti; rti; rti; rti; rti; rti; rti; rti; rti; rti; rti; rti; rti; rti; rti; rti; rti; rti; rti; rti; rti; rti; rti; jump fir; rti; rti; rti; rti; rti; rti; rti;
main:
ena m_mode;
mr = 0;
I0 = simples;
L0 = length(simples);
I1 = coef;
L1 = length(coef);
M0 = 1;
M2 = 0;
ar = 4;
dm(0x3ffb) = ar;
ar = 999;
dm(0x3ffc) = ar;
dm(0x3ffd) = ar;
ifc = 0x00ff; nop;
ena timer;
imask = b#0000000001; nop;
end: jump end;
fir:
mr = 0;
CNTR = 79;
do c1 until CE;
mx0 = dm(I0, M0);
my0 = dm(I1, M0);
c1: mr = mr + mx0 * my0 (ss);
mx0 = dm(I0, M2);
my0 = dm(I1, M0);
mr = mr + mx0 * my0 (ss);
ax0 = IO(0);
dm(I0, M2) = ax0;
mr = mr (rnd);
if mv sat mr;
IO(1) = mr1;
rti;
5. Проверка
Проверим правильность работы фильтра. Для этого сформируем и подадим на вход фильтра сигнал длительностью в 1 секунду, имеющий постоянную амплитуду и линейное нарастание частоты от 0 до 4 кГц.

Рисунок 9 - ЛЧМ сигнал на входе фильтра
После отработки программы на выходе фильтра получим сигнал, совпадающий с заданной АЧХ:
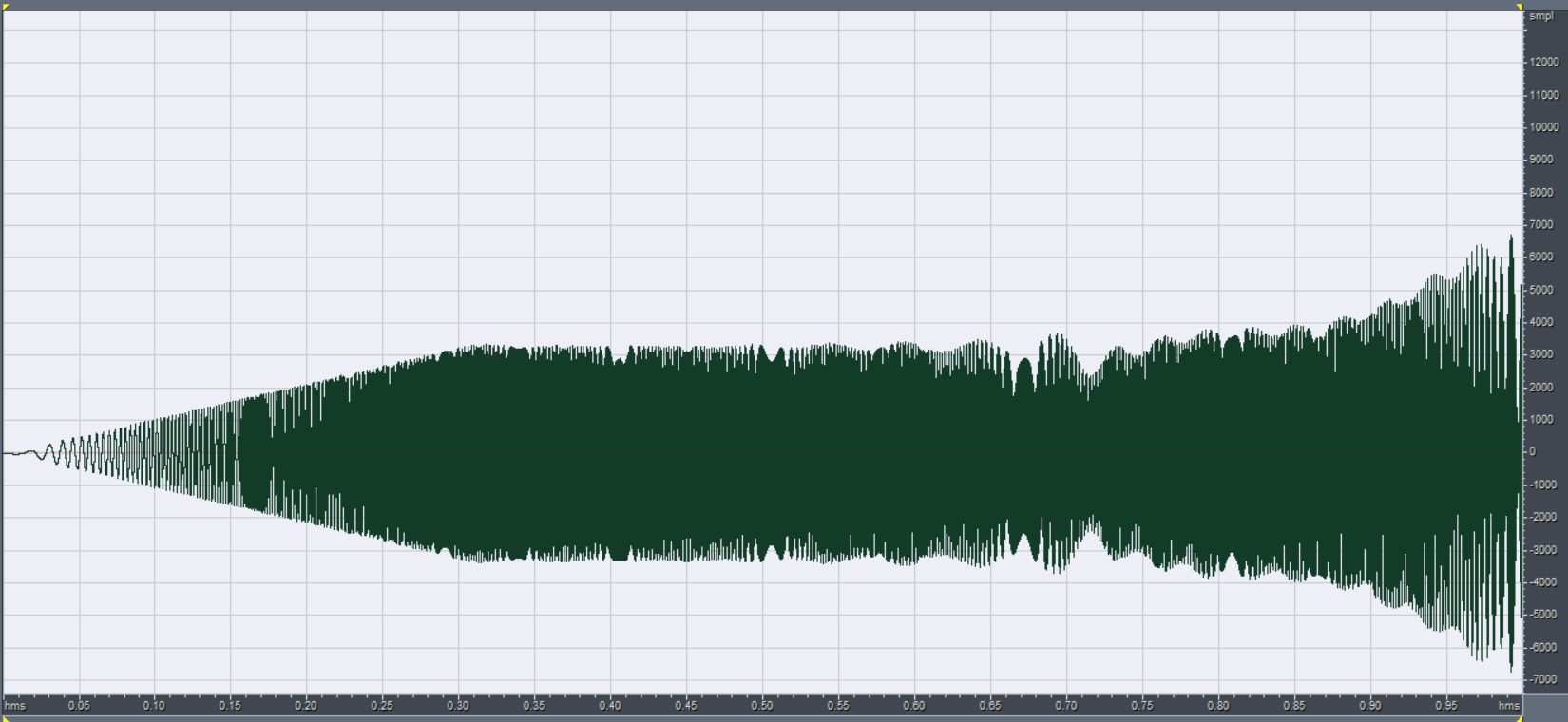
Рисунок 10 – ЛЧМ сигнал на выходе фильтра
Москва 2023
