lr_10

1. Министерство цифрового развития, связи и массовых коммуникаций российской федерации

2. Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

3. Московский технический университет связи и информатики

4. Кафедра многоканальных телекоммуникационных систем

5. ЛАБОРАТОРНАЯ РАБОТА

6. № 10

8. по дисциплине

9. Цифровые системы передачи и методы их защиты

11. на тему

13. РЕАЛИЗАЦИЯ ОПЕРАЦИИ УМНОЖЕНИЯ В расширенных ПОЛЯХ ГАЛУА

17. Выполнил:

18. студент гр. БЗС2002 Ломакин А. А.

20. Проверила:

1. Ст. пр. Мусатова О.Ю.

5. Москва 2023

7. 1. Постановка задачи

8. Средствами сигнального процессора ADSP-2181 реализовать в расширенных полях Галуа базовую криптографическую операцию умножения:

9. Z = ( A * B ) mod ( xⁿ+ x + 1 ),

10. где число А – сигнал с порта IO(0);

11. число В – значение из памяти данных;

12. (xⁿ + x + 1) – полином n-ой степени, n=15;

13. результат Z вывести в порт IO(1).

15. При реализации использовать признак AC.

16. Рассмотреть два варианта реализации: вариант №1 — со сдвигом полинома и числа на 1 разряд влево; вариант №2 — сдвиг полинома выполняется с использованием команд EXP и NORM

18. 2. Исходные данные

19. Исходные данные представлены в таблице 1

21. Таблица 1 — Исходные данные

    № ПК	Задание X = ( A * B ) mod ( xn+ x + 1 )
    6	X =( 3264*50) mod ( xn+ x + 1 )

24. 3. Блок-схемы алгоритмов

Блок-схема алгоритма, реализующего операцию умножения в расширенных полях Галуа со сдвигом полинома и числа на 1 разряд влево (вар. №1), представлена на рисунке 1.

Блок-схема алгоритма, реализующего операцию умножения в расширенных полях Галуа со сдвигом полинома и числа с использованием команд EXP и NORM (вар. №2), представлена на рисунке 2.

25. 

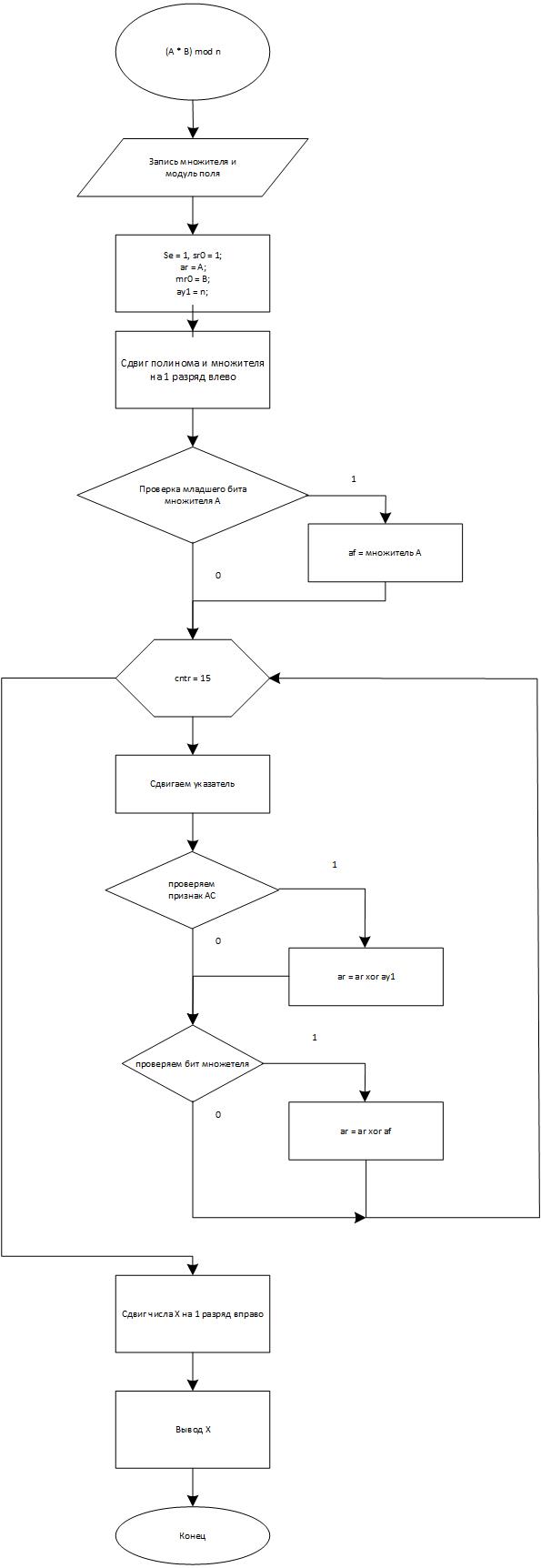
26. Рисунок 1 - Блок-схема алгоритма, реализующего операцию умножения в расширенных полях Галуа со сдвигом полинома и числа на 1 разряд влево

27. 

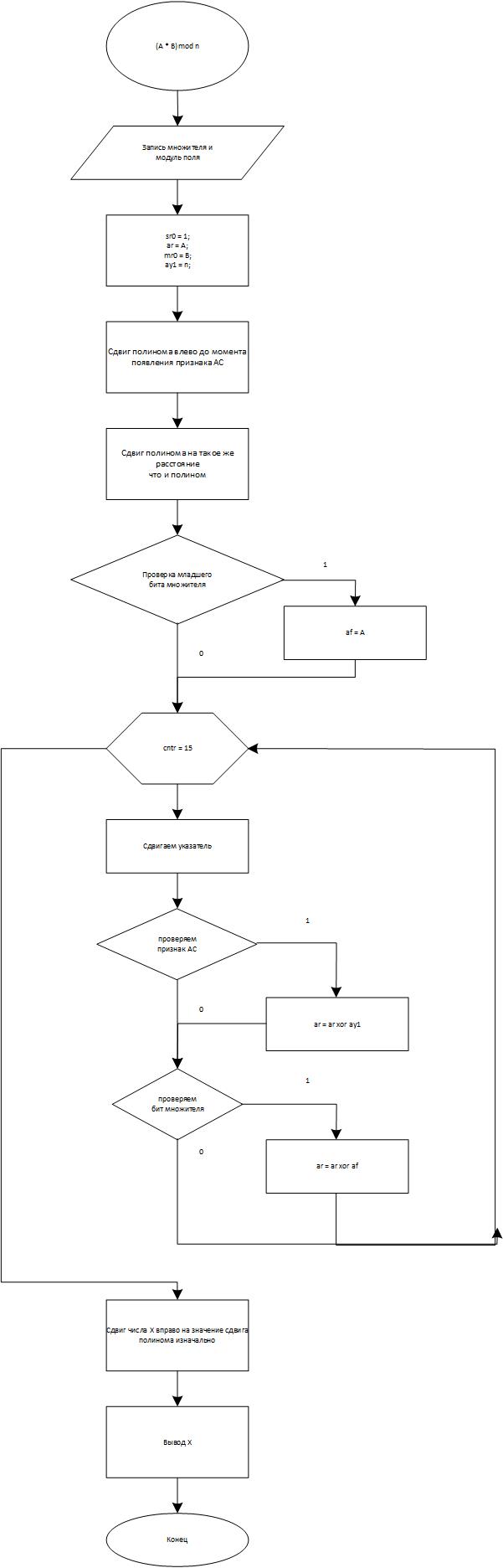
28. Рисунок 2 - Блок-схема алгоритма, реализующего операцию умножения в расширенных полях Галуа со сдвигом полинома и числа с использованием команд EXP и NORM

29. 4. Исходный текст программы

.section/dm vars; .var n1 = 32771;//(x^15 + x + 1) .var n2 = 17475;//(x^14 + x^10 + x^6 + x + 1) .var A = 3264; .var B = 50; .var otvet; .section/pm varsp; .section/pm program; ar = dm(A); mr0 = dm(B); call umn1; dm(otvet) = ar; //Рассматриваем когда полином имеет старшую степень 2^15 //и мы должны его сдвинуть на 1 влево вместо с множителем umn1: ay0 = 0; se = 1; af = pass ay0; sr0 = dm(n1); sr = lshift sr0(lo); ay1 = sr0; sr = lshift mr0(lo); mr0 = sr0; sr0 = 1; se = 1; ay0 = sr0; none = mr0 and ay0; if NE af = pass ar; CNTR = 15; do cicle2 until CE; sr = lshift sr0 (lo), ay0 = ar; ar = ar + ay0; ay0 = sr0; if ac ar = ar xor ay1; none = mr0 and ay0; cicle2: if ne af = ar xor af; ar = pass af; sr = lshift ar by -1(lo); ar = sr0; RTS; //Рассматриваем когда полином имеет старшую степень 2^14 и меньше //и мы должны его сдвинуть и множитель на столько позиций,чтобы он вышел //в признак AC umn2: ay0 = 0; mx1 = ar; af = pass ay0; sr0 = dm(n2); se = exp sr0(hi); ar = se; ar = ar - 2 ; se = ar; sr = norm sr0(hi); ay1 = sr1; sr = norm mr0(hi); mr0 = sr1; ax1 = se; ar = mx1; sr0 = 1; se = 1; ay0 = sr0; none = mr0 and ay0; if NE af = pass ar; CNTR = 15; do cicle3 until CE; sr = lshift sr0 (lo), ay0 = ar; ar = ar + ay0; ay0 = sr0; if ac ar = ar xor ay1; none = mr0 and ay0; cicle3: if ne af = ar xor af; ar = pass af; se = ax1; sr = lshift ar(hi); ar = sr1; RTS;

5. Анализ результатов

1 программа

Ручной

(3264 * 50*x) mod ((x¹⁵+x+1)*x)

0000 1100 1100 0000 * 0 0000 0000 0110 0100 = 10 1001 1011 0000 0000

1 0100 1101 1000 0000 mod(x¹⁶ + x²+x)

10 1001 1011 0000 0000 xor 10 0000 0000 0000 1100 = 1001 1011 0000 1100

После сдвига обратно 0100 1101 1000 0110

Программный

Заносим значения

Получаем ответ в AR

2 программа

Ручной

Первоначально сдвигаем образующий полином так, чтобы было переполнение AC, следовательно полином x¹⁴+ x¹⁰ + x⁶ +x + 1 нужно сдвинуть на разряд влево для того , чтобы было переполнение.

(3264 * 50) mod (x¹⁴+ x¹⁰ + x⁶ +x + 1)

x¹⁴+ x¹⁰ + x⁶ +x + 1 для решения мы должны наш полином сдвинуть в AC, следовательно на 2 регистра получается мы образуем его

в x¹⁶+ x¹² + x⁸ + x³+ x²

Следом мы сдивагаем и наш множитель

0000 1100 1100 0000 * 00 0000 0000 1100 1000 = 101 0011 0110 0000 0000

101 0011 0110 0000 0000 mod((x¹⁶+ x¹² + x⁸ + x³+ x²))

101 0011 0110 0000 0000 mod 100 0100 0100 0011 0000 = 0110 0011 0011 1100

После сдвига обратно 0001 1000 1100 1111

Программный

Заносим значения

Получаем ответ в AR

6. Вывод

Средствами сигнального процессора мыADSP-2181 реализовали в расширенных полях Галуа базовую криптографическую операцию умножения:

32. X = ( A * B ) mod ( xⁿ+ x + 1 ),

33. Исходя из анализа, можно сказать, что программа работает

правильно, так как ручной расчёт аналогичен программному расчёту, при сдвиге числа на nразрядов результат так же сдвигается на nразрядов.