
МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ордена Трудового Красного Знамени федеральное
государственное бюджетное образовательное
учреждение высшего образования
«Московский технический университет
связи и информатики»
────────────────────────────────────
Кафедра ИТ
Лекция по теме «компьютерное зрение»
по дисциплине «Информационные технологии и программирование»
Выполнили: студ. гр. БЗС2002
Ломакин Алексей
Протасова Татьяна
Умаров Кирилл
Проверила: доцент
Пчелкина Н. В.
(Осенний семестр)
Москва 2022
Содержание:
Кафедра ИТ 1
Лекция по теме «компьютерное зрение» 1
по дисциплине «Информационные технологии и программирование» 1
Азы работы с изображениями 24
1. Азы работы с изображениями 24
1.1. Попиксельная обработка изображений 24
25
Какой-то вводный слайд 25
1.2. Задача маттинга и морфология 42
42
Слайд 22 42
Время на реальном примере попробовать приобретенные навыки. Рассмотрим задачу Маттинга. Она формулируется довольно абстрактно – у нас есть изображение, на котором есть какой-то основной объект и фон. Нам необходимо построить маску, которая отражала бы, где на изображении находится этот основной объект. Сразу же можно обратить внимание, что маска не абсолютно-белого цвета – у нас имеются промежуточные значения в волосах, т.к. волосы принадлежат одновременно и объекту, и фону. Задача Маттинга как раз и решает проблему поиска маски. 42
43
Слайд 23 43
Рассмотрим более тривиальный случай задачи Маттинга – задачу зеленого экрана. Мы попробуем построить какой-то алгоритм, который не будет идеальным, но будет работать. Наша задача – взять из изображения и выделить все пиксели, где цвет зеленый. Для этого построим гистограмму Hue-значений в HSV формате. Мы увидим, что на гистограмме будет огромный всплеск среди значений. Этот всплеск как раз и относится к зеленому цвету. Если его обрезать, то мы получим: 43
44
Слайд 24 44
Все пиксели, где Hue меньше определенного и больше определенного значений это человек, а между ними – зеленый цвет. Мы получили маску. Она сделала то, что нужно – выделила человека, но в ней есть куча дыр. Эти дыру нужно как-то исправить и тут нам на помощь приходит морфология: 44
45
Слайд 25 45
Морфология – это работа с бинарными изображениями. Бинарное изображение – такое изображение, где есть только 2 значения 0 или 1. Наша маска являлась бинарным изображением – пиксель либо принадлежал диапазону, либо нет. Бинарные изображения практически никогда не используются для реального отображения чего-либо, а используются в промежуточных вычислениях, как раз для таких моментов, когда в алгоритме возникает задача профильтровать пиксели по какому-нибудь критерию. 45
46
Слайд 26 46
Первая операция – это эрозия. Эрозия формирует из одного изображения новое, записывая в значения пикселя в новом изображении минимум из значений соседей этого же пикселя на предыдущем изображении. Сосед – это параметр, например в текущем примере это тот, кто граничит ребром. 46
47
Слайд 27 47
Применим эрозию на реальной картинке. Видно, что наша буква уменьшилась. Отсюда и названия эрозии – если наш объект белый, то эрозия его сожмет. 47
47
Слайд 28 48
Следующая операция аналогична и называется наращиванием. Теперь мы берем не минимум, а максимум. В этом случае расширяются не черные области, а белые. 48
48
Слайд 29 48
На примере той же буквы мы видим, что наращивание называется наращиванием, потому что если наш объект белый, то применение этой операции его увеличит. 48
49
Слайд 30 49
Теперь рассмотрим более сложную операцию – бинарное открытие. Это просто последовательное применение двух операций – эрозии и наращивания. Вначале мы уменьшим изображение, а затем увеличим. В результате мы удалим тонкие элементы на изображении. Например, в данном случае удалилась палка буквы. 49
49
Слайд 31 49
Аналогичная операция – бинарное закрытие, только теперь мы сначала применяем наращивание, а потом эрозию. Это нужно, чтобы закрыть черные дыры. 50
50
Слайд 32 50
Эта именно та операция, которая нам нужна. Если применить бинарное закрытие к той маске, которую мы получили, то уйдут все дыры. 50
51
Слайд 33 51
Теперь поговорим про RGBA. А – отвечает за альфа канал, то есть за прозрачность. В целом его можно добавить не только к цветовой схеме RGB, а вообще к любой и таким образом хранить информацию, где на изображении находится фон, а где находится объект. По зеленому экрану мы нашли, где находится человек, а где фон. Мы можем записать человека в альфа канал, таким образом добавив прозрачности к нашему изображению. Что у нас получится в итоге? 51
52
Слайд 34 52
В итоге у нас получится изображение без фона. В целом альфа канал можно использовать и для смешивания изображений, например взять и заменить фон, что часто используется для монтажа видео. 52
1.3. Свертки 52
До этого момента мы говорили в основном о попиксельных операциях – операциях, которые используют только один пиксель и как-то его изменяют. Теперь время начать использовать в наших функциях сразу несколько пикселей. 52
53
Слайд 35 53
Начнем с самого простого – будем идти по нашему изображению окошком и записывать в пиксель нового изображения среднее значение из пикселей в нашем окошке. Для цветных изображений мы делаем то же самое, но для каждого канала независимо. Давайте посмотрим на результат: 53
54
Слайд 36 54
Для черно белого изображения – изображение стало более мутным. Для цветных то же самое – цвет не потерялся, но качество изображения ухудшилось. Давайте более внимательно посмотрим на объекты вблизи: 54
55
Слайд 37 55
Если присмотреться к объекту, у которого очень четкие границы, то можно заметить артефакты. Конкретно здесь артефакт называется «звенящим артефактом». Он заключается в том, что четкие границы объекта размазываются и становятся повторяющимися и «призрачными». Если мы хотим добиться размытия изображения, то это точно не тот эффект, который нам нужен. Появляются артефакты буквально из-за усреднения, т.к. мы усредняем все пиксели с одинаковыми весами в независимости от того, на каком расстоянии они находятся от центрального. Решением проблемы такого артефакта будет усреднение тем же окном, но взвешенно. 55
55
56
56
Слайд 38 56
Такое взвешенное усреднение называется сверткой. Свертка - это такая же операция, где мы идем скользящим окном, но теперь мы записываем не просто среднее значение, а взвешенное среднее значение с какими-то весами и делаем так для каждого канала независимо. Но какие веса нам надо выбрать, если мы хотим замылить наше изображение и при этом не породить артефакты. 56
57
Слайд 39 57
Классическим выбором является фильтр гаусса. Мы чуть позже разберем, что это такое, а пока просто посмотрим на то, как он работает. На слайде мы видим, что изображение стало более мутным, но при этом артефактов не возникло и можно хорошо разглядеть объект. 57
57
Слайд 40 57
Что же такое фильтр гаусса? Идея в том, чтобы взять двумерное гауссовское распределение – это такой купол, где есть мода, значение распределения в которой максимально и этот купол очень быстро уходит вниз и чем дальше мы находимся от моды, тем ближе к нулю веса пикселей. 57
58
Слайд 41 58
Если нарисовать гауссовское распределение, то мы получим следующий белый размытый кружок. 58
58
Слайд 42 58
Проблема гауссовского распределения в том, что в теории оно бесконечно и если мы захотим усреднять наши пиксели именно с ним, то нам придется для каждого пикселя усреднять всю картинку. Но за счет того, что гауссовское распределение очень быстро убывает и через какой-то момент времени становится очень близким к нулю мы можем брать окно размером 6 сигма, потому что после него значения настолько незначительны, что практически не влияют на итог. На примере гауссовский фильтр размером 3 на 3, т.е. сигма здесь ½. 58
59
Слайд 43 59
Собственно, мы берем наше изображение, применяем к нему гауссовский фильтр и получаем результат, который мы видели несколько слайдов назад. 59
59
Слайд 44 59
Свертки используются очень и очень часто – это одна из самых ключевых операций в компьютерном зрении, которая применяется практически везде и делает очень много всяких полезных штук. Например, свертки могут показать нам границы, т.е. те места, в которых объекты меняются (один объект сменяет другой). Зачем и как искать границы мы разберем чуть позже, а пока на слайде показан пример работы сверток в выделении границ. 59
60
60
Слайд 45 60
Также свертки могут применяться для стилизации изображений, как, например, контрастность в попиксельных операциях, или же применяться для размытия изображений, как во время движения руки при записи видео на камеру. Зачем это вообще нужно? Такое бывает полезно, когда мы учим какой-то алгоритм (нейронную сеть) и хотим, чтобы она училась работать на таких изображениях. Мы берем нормальное изображение, каким-то образом портим его и получаем уже несколько изображений для обучения нейронных сетей. Такой метод называется аугментацией, но подробнее об этом мы поговорим позже. 60
61
Слайд 46 61
Настало время поговорить о свойствах сверток. Самое очевидное из них – то, что они уменьшают размер изображения. Почему так происходит? Потому что мест, куда мы можем приложить наше ядро свертки (окно, по которому мы идем по изображению) просто меньше, чем количество пикселей. Соответственно, наше итоговое изображение немного уменьшается. 61
62
Слайд 47 62
Если мы хотим избежать этого эффекта, т.е. хотим, чтобы наша свертка была такого же размера, как исходное изображение, мы можем воспользоваться паддингом. Паддинг – это просто обивка нашего изображения временными пикселями, которые нужны для того, чтобы количество мест, в которые мы можем приложить свертку, увеличилось и уменьшение изображения съело бы пиксели паддинга, но оставило оригинальные. Паддингов бывает много типов. Самый простой – это константный, когда мы просто взяли и обили наше изображение временными пикселями. Конкретно этот вариант часто применяется в нейронных сетях. Самый продвинутый вариант – симметричный. Тут мы отражаем нашу картинку вдоль оси, которую мы хоти обить. 62
63
Слайд 48 63
Следующее свойство сверток – невосприимчивость к сдвигу. Это свойство будет важно, когда мы будем говорить о нейронных сетях, но понять его можно уже сейчас. Что это значит? Это значит, что где бы не находился объект на нашем изображении свертка обработает его одинаково. Будь он в левом углу или в правом. Потому что мы идем скользящим средним и применяем его в независимости от того, где мы находимся. 63
63
Слайд 49 63
Еще одно свойство – комбинация сверток – свертка. Почему так? Свертка – это линейная операция, а комбинация двух линейных операций тоже линейна, соответственно, комбинация двух сверток тоже свертка. Давайте рассмотрим это на примере. У нас есть два ядра сверток – одно вертикальное, другое горизонтальное. Мы можем записать их как формулы. В формулах нижний индекс это движение по горизонтали, верхний – движение по вертикали. Соответственно, мы можем записать новую формулу, которая будет последовательным применением двух наших формул. В итоге мы снова получим какую-то формулу, в которой опять будет линейная операция и эта линейная операция будет в окне, просто чуть большего размера. Эту линейную операцию мы сможем записать как свертку. 63
64
Слайд 50 64
Из линейности вытекает еще одно свойство, которое доступно не всем сверткам, а именно сепарабельность. Сепарабельность – возможность разложить нашу свертку на какие-нибудь две. В нашем примере итоговая свертка сепарабельна, потому что она раскладывается на две независимые свертки, одна из которых горизонтальна, а другая вертикальна. Зачем это нужно? Это нужно для прироста скорости. Давайте посчитаем конкретно на этом примере. Если мы применим итоговую свертку, то мы применим 9 операций (9 весов), а если мы применим вертикальную и горизонтальную, то мы сделаем всего 6 операций. Это может стать важным на масштабе сверток – допустим у нас свертка не 3 на 3, а 9 на 9, тогда мы сделаем 18 операций против 81. 64
65
Слайд 51 65
Вот мы и поговорили о свертках. Поняли, где они могут применяться и что могут делать сами по себе. Давайте попробуем сделать с ними что-то интересное и полезное. Для этого посмотрим на портретную съемку. Портретная съемка делается с помощью профессиональных камер, на которую в результате съемки человека получается красиво размытый задний фон (эффект Боке). 65
66
Слайд 52 66
Эффект Боке доступен далеко не для всех камер. На самом деле для профессиональной съемки покупаются специальные камеры, заточенные на то, чтобы снимать людей с определенного расстояния и в итоге получать красивое размытие. На слайде пример фотографии одного и того же объекта, но на разные камеры. У одного присутствует эффект Боке, у другого нет, потому что это буквально физическое свойство камеры. Большая часть камер сейчас – камеры мобильных телефонов. В них эффект Боке недоступен и, скорее всего, никогда не будет доступен, потому что это физическое свойство камеры, которое требует, чтобы камера была большой, а в телефоне физически нет места для такой. Остается только имитировать этот эффект. 66
67
Слайд 53 67
Как мы будем это делать? Мы найдем человека на изображении так же, как мы делали для зеленого экрана, но в этом случае воспользуемся каким-то готовым решением и предположим, что у нас уже есть готовая маска. Вторым шагом мы размоем наше исходное изображение, таким образом размыв человека и фон. Затем подставим в наше оригинальное изображение размытый фон и таким образом сэмитируем эффект Боке. 67
67
68
68
68
69
69
Слайд 54 69
Вот фотография. Мы вытаскиваем маску, после чего удаляем фон (это будет та часть картинки, которая не изменится. Затем размываем наше изображение и инвинтируем маску. Теперь наоборот вырежем человека и оставим фон. После просто сопоставляем. В итоге мы с имитировали сложное физическое свойство камеры просто используя алгоритмы. 69
2. Базовые алгоритмы над изображениями 69
2.1. Интерполяция 69
Поговорим про интерполяцию. Интерполяция нужна для изменения геометрии изображения. Что же это значит? Сейчас узнаем: 69
70
Слайд 55 70
Давайте посмотрим на наше изображение как на функцию. Функция получается дискретная. В целочисленных значениях мы можем знать значение пикселя. Но что если мы захотим узнать значения между пикселями, т.е. сделать нашу функцию непрерывной. Если мы делаем нашу функцию непрерывной, то тогда мы будем точно знать значения в очень конкретных местах (в серединах нашего пикселя). Там мы гарантированно даем ответ – просто из нашей дискретной функции вытаскиваем его. Но как нам ответить на вопрос «что находится между ними?» Самый простой способ – это метод ближайшего соседа. Метод ближайшего соседа в том, что мы для нашего нецелочисленного значения находим ближайшее целочисленное значение и говорим, что значение здесь соответствует значению в ближайшем целочисленном. Наша картинка от этого вообще не меняется и фактически получается ровно то отображение, которое было изначально. 70
71
Слайд 56 71
Давайте теперь в таких формулировках попробуем изменить размер нашего изображения. То есть, как например на слайде, мы из изображения 5 на 5 попробуем сделать изображение 7 на 7. Значит нам нужно как-то заполнить наши новые пиксели в разрешении 7 на 7: 71
71
Слайд 57 71
Что нужно сделать для этого? Нужно взять координатную сетку изображения 7 на 7 и наложить на исходное изображение. Получим новую сеточку: 72
72
Слайд 58 72
Давайте в новой сетке расставим точки аналогичные тем, которые мы расставляли, когда говорили про интерполяцию. Это будут те точки, в которых нам необходимо узнать значение, чтобы сделать наш оверсайз (увеличение разрешения). Эти точки находятся далеко не в центрах исходного изображения. Соответственно нам нужно понять какое значение в них записывать. Важное замечание перед тем, как мы начнем использовать уже нам знакомый метод ближайшего соседа это то, что чтобы воспользоваться методом ближайшего соседа (и вообще любой интерполяцией) нам необходимо сопоставить координаты исходного изображения с координатами нового изображения. Для этого мы должны сопоставить их углы. Углы будут находится в -1/2 и -1/2. Так происходит потому что т.к. наше изображение было дискретной функцией, точка 0 0 отвечала за центр пикселя, в то время как угол находится немножко выше и левее и там будет точка -1/2 -1/2 и совмещать мы должны конкретно по этой точке. 72
73
Слайд 59 73
Теперь, когда мы разобрали такой технический момент, мы можем воспользоваться интерполяцией – просто взять, найти ближайшую целочисленную точку и из нее вытащить значение. Вот что получится: 73
73
Слайд 60 73
В целом, получилось неплохо. Но, как можно заметить, изображение изменилось, изменились пропорции. Конечно же можно сделать и лучше. 73
74
Слайд 61 74
Лучше можно сделать с помощью билинейной интерполяции. Идея в том, чтобы вытаскивать значения не из одного пикселя, а усреднять из соседних пикселей. Как работает билинейная интерполяция? Для начала рассмотрим одномерный случай, т.е. линейную интерполяцию, когда у нас функция одномерная (просто прямая). В данном случае мы, чтобы найти значение в новой точке, берем значения в ее соседях и усредняем пропорционально расстоянию до этого соседа (т.е. чем расстояние больше, тем вес у цвета меньше). 74
75
Слайд 62 75
Перенесем эту идею на двумерный случай (для картинок). Получим билинейную интерполяцию. На самом деле билинейная интерполяция – это просто 3 линейных интерполяции. Мы берем нашу точку, находим 4 соседних пикселя, в начале усредняем одну пару из них, потом вторую и затем усредняем наши усреднения. Итого 3 операции. 75
76
Слайд 63 76
Итак, что мы будем делать? Мы будем находить координату желаемого пикселя и считать его значение по четырем соседям. Здесь есть одна проблема – в пикселях, которые находятся на краях, потому что для них может не найтись 4 соседей. Например, для левого верхнего угла у нас вообще будет только один сосед, т.к. в округе только один пиксель. Что нужно сделать в таком случае? 76
76
Слайд 64 76
Воспользоваться уже знакомым нам паддингом – обить наше изображение временными пикселями которые мы будем использовать для усреднения в тех местах, где есть недостаток в соседях. Теперь у нас все готова для применения билинейной интерполяции, посмотрим на результат: 76
77
Слайд 65 77
Получилось вот такое изображение. Здесь уже получше с пропорциями, лучше угадывается какое изображение было исходным. В целом, билинейная интерполяция - это классический выбор, когда мы пишем алгоритмы. Чаще всего применяется она, но справедливости ради нужно упомянуть об артефактах: 77
77
Слайд 66 77
Артефакты возникают, когда мы очень сильно хотим увеличить разрешение, например с 5 на 5 до 700 на 700. В этом случае мы получим артефакты в виде звездочки. Скорее всего, такого сильного увеличения разрешения не потребуется в обычных задачах, но можно применить и бикубическую интерполяцию, которая поможет избавиться от артефактов. А пока давайте сделаем небольшой вывод про билинейную интерполяцию – она работает быстро (здесь присутствует всего 3 операции и за счет этого она используется чаще всего). Этот алгоритм чаще всего используется в промежуточных вычислениях и в целом применяется чаще всего. Но так что за бикубическая интерполяция? 77
78
Слайд 67 78
Мы не будем подробно разбирать бикубическую интерполяцию, скажем только, что делается она за счет последовательного применения сплайнов. Важно обратить внимание на количество операций, которое здесь требуется – вначале мы строим 4 сплайна по 4 точкам, затем по ним строится финальный сплайн, откуда берется итоговое значение. В сравнении с билинейной интерполяцией это очень долгий процесс и поэтому бикубическую интерполяцию практически не используют в алгоритмах. 78
79
Слайд 68 79
В результате применения бикубической интерполяции к сильному увеличению разрешения мы сможем избавиться от артефактов в виде звездочек. Если делать небольшой вывод по такой интерполяции, то можно отметить, что она практически не используется в алгоритмах, а применяется только в фоторедакторах, где важно сохранить максимальное качество в ущерб скорости. 79
79
Слайд 69 79
Теперь поговорим об уменьшении разрешения. Самый простой способ как мы можем это сделать – это взять нашу сетку на новом изображении, подставить ее в старое изображение и по координатам нужной интерполяции вытащить значения. Получается что-то такое: 79
80
80
Слайд 70 80
Если присмотреться, то можно заметить, что появились артефакты. Такие артефакты называются алиасингом (очень резкие переходы). Они возникают из-за того, что далеко не все пиксели участвуют в интерполяции, т.е. мы можем спокойно с таким подходом окно 5 на 5 перевести в 1 пиксель и при этом воспользоваться только 4 пикселями и потерять кучу информации, в результате чего переходы становятся очень резкими. Как решить эту проблему? Нам нужно сглаживать изображение до понижения разрешения, т.е. мы будем понижать теми же шагами, но перед тем, как вытаскивать координаты на старом изображении мы сгладим наше старое изображение, т.е. пройдем фильтром гаусса и получим замыленное изображение: 80
81
Слайд 71 81
В итоге артефакты уходят. В целом, чтобы артефакты ушли, можно делать сглаживание и после интерполяции, но в таком случае мы получим слишком замыленное изображение, а если сделать до, то мы уберем артефакты и оставим нормальное разрешение. Такая дополнительная операция называется анти-алиасингом. 81
81
Слайд 72 81
Еще раз посмотрим на разницу если мы делаем размытие и если не делаем. Что мы можем сделать с изображением еще? 81
82
82
Слайд 73 82
Мы можем поворачивать изображения. Казалось бы, причем тут интерполяция, но повернутое изображение на самом деле выглядит как картинка с черными рамками, просто все черное здесь имеет в альфа канале полную прозрачность. Если задуматься, то можно понять, что при повороте у нас не будет однозначного соответствия между пикселями – пиксели попадут в промежутки между целочисленными значениями и их придется как-то приближать. 82
83
Слайд 74 83
Еще можно делать аффинные преобразования, т.е. изменять геометрию изображения. 83
83
Слайд 75 83
Для всех этих применений интерполяции схема примерно одинаковая. Мы для каждого пикселя на генерируемой картинке будем находить координаты этого пикселя на исходной. Важно, что именно в таком порядке – что мы будем искать координаты новых пикселей на исходной картинке, потому что иначе мы не закроем все дыры. Затем мы считаем значение интерполяции. 83
2.2. Фильтрация 84
2.3. Гистограммы 89
Границы и признаки 100
3. Границы 100
3.1. Оператор Собеля 100
Что такое границы? Это пиксели, на которых заканчивается какой-либо объект. 100
Можно отметить, что на границах резко меняется яркость изображения. То есть, если представить изображение как функцию, то на границах происходит резкий скачек функции. Обычно для поиска этого скачка используют производную, но для изображения такой способ не подходит, поэтому посчитаем приближенно, считая разницу функции в точках, соседних нашей. 100
101
101
Представление в виде свертки: 101
102
Далее необходимо сгладить изображение, чтобы убрать резкие изменения в функции, не относящиеся к объектам. 102
Итоговое изображение с инвертированным цветом: 103
Изображение выглядит «дырявым» из -за того, что мы использовали производную по одной оси. Объеденим производные по двум осям: 103
Итог: 103
3.2. Оператор Лапласа 104
В операторе Лапласа мы используем вторую производную, а именно свойство, что изменения максимально сильны при пересечении 0. 104
Вторая производная: 105
Для объединения двух производных мы используем оператор Лапласа: 105
Итог: 106
Этот способ: 106
Чувствителен к шуму 106
Хорошо работает на ядрах 5х5 - 9х9 106
3.3. Canny 107
Canny – лучший алгоритм выделения границ. Он строит ровные границы объектов. 107
Canny состоит из: 107
1. Фильтрации 107
2. Подсчета градиента 107
3. Подавления немаксимумов 107
4. Фильтрации границах 107
5. Объединения в линии 107
Фильтрация — используем фильтр Гаусса. 107
Подсчет градиента — используем оператор Собеля. На этом шаге мы запоминаем магнитуду и направление градиента. 107
Подавление немаксимумов нужно для того, чтобы у нас вместо неявной границы появилась четкая. 107
Алгоритм подавления: 108
Фильтрация границ — частичная фильтрация уже произошла во время подавления, но этого не достаточно. Для дополнительной фильтрации мы делим все пиксели на границе на 2 категории: сильная и слабая границы. 108
Сильные границы мы обозначаем как границы, слабые границы мы добавляем в границы, если среди 8 ближайших пикселей есть минимум 1 граница. 108
4. Пирамиды и признаки 108
4.1. Пирамиды 108
Пирамиды — структуры данных для хранения изображений. Хранит изображения в разных разрешениях. 108
Пирамида Гаусса 108
В пирамиде Гаусса каждое следующее изображение в 4 раза меньше предыдущего. 109
Формула пирамиды Гаусса. 109
Пирамида Лапласа: 109
Пирамида Лапласа на i шаге — это разница пирамиды Гаусса на i шаге и ее сглаженной версии. 109
Минус — пирамида не инвертируема — нельзя восстановить изображение. 110
Но в немного другом варианте пирамиды мы убираем этот недостаток. 110
Зачем применяются пирамиды? Они используются для объединения изображений. 110
Задача классификации для нейронных сетей 111
5. Задача классификации 111
5.1. Классификация изображений и ImageNet 112
Классификация - определение класса объекта. 112
Классификации присущи стандартные вызовы: 112
Многоклассовая классификация — когда мы выбираем какой класс из большого набора является верным для объекта. 112
Пересекающиеся классы — когда на изображении находятся несколько объектов, чьи классы нужно определить. 112
Несбалансированные классы — когда для одного класса изображений много, а для другого очень мало. 112
Шум в разметке — когда на изображениях присутствует шум. 112
Слайд-? 112
Но у задач классификации в компьютерном зрении есть свои особенности: 112
Наш алгоритм должен быть чувствительным к сдвигам, то есть, где бы не находилась на изображении кошка, класс у нее не изменится. 112
Наш алгоритм должен быть устойчив к изменению освещения, так как оно сильно меняет изображение объекта. 112
Наш алгоритм должен классифицировать объект вне зависимости от его положения, например, сидящая и лежащая кошка имеют один класс. 112
Наш алгоритм должен быть устойчив к перекрытию объектов, то есть часть туловища кошки — тоже кошка, даже если голова закрыта чем — либо. 113
Наш алгоритм должен учитывать вариативность внутри класса, ведь кошки разных пород все равно имеют один класс! 113
Метрики для задач классификации: 113
Слайд-? 113
ImageNet – самый знаковый датасет в компьютерном зрении. Он содержит почти 22 тысячи классов. Например, для каждой породы собак — свой класс. Но для обучения чаще всего используют 1000 классов. 113
Слайд? 114
Есть другие, менее распространенные датасеты:MNIST используют для распознавания рукописных текстов и т.д. 114
5.2. Базовые слои и оптимизация 114
Сверточные слои — применяются в компьютерном зрении, так как не чувствительны к сдвигу и применяются не к каждому каналу по отдельности, а ко всем сразу, что экономит много ресурсов. Получается , что итоговые веса — высота свертки * ширину свертки * глубину входного канала * глубину выходного канала. 114
Слайд? 115
Еще одним преимуществом сверточных слоев является то, что их можно применять с зазором, то есть не ко всем кусочкам изображения, а к каждому второму. Это позволяет нам понизить размерность изображения. 115
Слайд? 117
Еще один способ понизить размерность изображения - разделить его на области 4*4 и брать из этой области самое высокое значение. Таким образом мы оставляем самые важные значения и выкидываем неважные. 117
Слайд? 117
Самая популярная промежуточная активация в компьютерном зрении — ReLU 118
У нее есть неприятная особенность — если на слое все признаки выдадут 0 или меньше, то активация все признаки приравняет к 0, из-за чего все признаки у следующих слоев автоматически станут равны 0. 118
Слайд-? 118
Следующим слоем является Dropout, который создает подсети, случайно выключая активации. Выключение активации — приравнивание ее к 0. 118
Он нужен для регуляризации, то есть когда при реальных условиях сеть ведет себя намного хуже, чем при тестах. Но минус этого слоя — сильное замедление работы сети. 118
Слайд? 119
У нас получилась итоговая схема обучения: 119
5.3. FLOPs & FoV 120
У нейронных сетей есть определенный набор характеристик: 120
FLOPs – Floating Point Operations – количество операций, необходимых для прогона модели на одном примере. Этот параметр не прямо зависим со скоростью работы, хоть и сильно коррелирует. 120
FoV – этот параметр определяет, сколько признаков поучаствовало в формировании признака определенного слоя. При формировании признака слоя участвуют несколько признаков предыдущего слоя. Он помогает лучше понять архитектуру сети и ее работоспособность еще до начала обучения. Например, если мы хотим найти на изображении объект, а FoV конечного слоя нашей сети меньше размера этого объекта, то очень велика вероятность, что сеть не справится с поставленной задачей. 120
6. Архитектуры 121
6.1. VGG & BatchNorm 121
Первая архитектура, которую мы рассмотрим — это VGG & BatchNorm. 121
Она была представлена в 2014 году и представляет собой просто последовательность сверток, которые заканчиваются несколькими полносвязными слоями. Использовалась активация ReLU и Пулинг maxpool 2x2(понижение разрешения). Причем при понижении разрешения увеличивается количество каналов на наших промежуточных признаках. 121
У VGG есть много вариаций, например VGG 19 с 19 полновязными слоями. 121
Этот алгоритм показывал лучшие результаты среди VGG, его параметры занимали более 500 mb, но существенным минусом было время обучения — 3 недели. 121
6.2. Модели ResNet 122
Модели ResNet пришли на смену VGG, когда последние достигли пика своих возможностей. Суть этой модели — блоки(или слои), в которых есть несколько последовательно расположенных сверток, и в которых общий выход блока состоит из выхода последней свертки с прибавлением входа блока. 122
Этот метод позволяет создать сеть с 152 слоями и более устойчива к разным негативным эффектам. Благодаря этим слоям значительно сократилось время обучения сети, что является огромным плюсом ResNet. 122
6.3. XceptionNet & MobileNet 122
XceptionNet – быстрая и компактная архитектура сетей. 123
XceptionNet — суть архитектуры: мы так же используем блоки, но в них изначально увеличивается количество входных каналов с помощью свертки 1х1, после чего делим нашу карту признаков на большое количество более мелких. Получившиеся карты признаков мы используем в некотором количестве сверток 3х3, которые учатся независимо друг от друга, после чего формируем с их помощью 1 большой выход. 123
Эта архитектура сильно ускорила и сжала сеть. 123
6.4. MNAS 123
Мы рассмотрели некоторые архитектуры сетей, но как выбрать, какая из них в вашем случае будет наиболее эффективна. NAS – это автоматический выбор архитектуры сети в зависимости от задачи. Для этого мы обучаем отдельную сеть, которая будет выбирать архитектуру для остальных сетей. 123
6.5. EfficientNet 124
Все архитектуры сетей, которые мы рассматривали до этого, были сверточными, но в 2017 появился новый вид архитектуры — трансформеры, который используют для обработки текста. ViT относится именно к этому виду. Его идея заключается в использовании блока attention, который из поступивших значений должен выбрать самый важный признак. Алгоритм: для каждого признака Q и K перемножаются, после чего от получившегося значения берем SoftMaх, у нас получается число в диапазоне 0...1, к которому прибавляется 1. И в итоге V умножается на получившееся число. Далее сравниваются все получившееся значения и выбирается самое большее. Для нашего алгоритма блоки ставятся параллельно . 124
Минус алгоритма ViT заключается в том, что обучение требует слишком много ресурсов, но в будущем эта архитектура может стать лучше сверточной, так как появилась совсем недавно. 124
7. Практическая методология 124
7.1. Что делать если плохо учится? 125
До обучения сети нам нужно сделать несколько шагов. 125
1. На первом шаге мы должны выбрать правильный критерий качества — метрику, с учетом всех особенностей будущей сети. 125
2. На втором шаге мы выбираем базовую модель с учетом всех наших требований. 125
После мы уже можем начать обучение сети. 125
Как правильно выбрать базовую модель? 125
Сначала нужно попробовать найти базовую модель, которая применялось для задачи, схожей с вашей. Если такой модели не существует или вам она не подошла, создавайте самостоятельно прототип, и после его тестирования усложняйте модель. 125
После выбора базовой модели мы проверяем метрики на тренировочном и тестовом наборе данных. Если на тренировочном метрики нехороши, то мы меняем модель или обучение. Если же с ними все в порядке, но тесовые результаты оставляют желать лучшего, то мы добавляем данные, в противном случае меняем модель или обучение. 125
Как менять архетектуру? 126
Заранее сказать, какая модель покажет себя лучше невозможно, но есть вероятность верно предугадать по моделям, которые работали над похожими задачами. Это можно делать автоматически, что мы упоминали ранее, и вручную. Ручной метод более популярен. 126
При ручной настройке нужно учитывать следующие параметры: 127
Способность к обучению 127
Потребление памяти 127
Потребление времени на предсказании 127
Потребление времени на обучении 127
Ручное управление состоит том, чтобы сбалансировать эти характеристики под ваши нужды. 127
Отлавливание ошибок в машинном обучении очень тяжелая задача, так как они хоть и ужудшают результат обучения, но при неправильной работе одной части алгоритма другие могут подстроится и частично скомпенсировать ее, поэтому о ошибке можно вообще не узнать. 129
Практики отлавливания ошибок: 129
Визуализация работы во время обучения — выписывать все странные предсказания при обучении, часто так можно заметить ошибки. 129
Визуализация худших ошибок — мы отлавливаем моменты, где вероятность, предоставленная сетью была большой, но она совершила ошибку 130
Переобучение на маленьком наборе данных — если после полноценного обучения сеть выдает плохой результат, то перед сменой архитектуры или ее доработкой можно попробовать обучить ее на 10-15 изображениях. Если про таком наборе она все равно будет ошибаться, то ваша модель не обучается, где-то есть ошибка 130
7.2. Аугметация и Псевдо-разметка 130
Мы рассмотрели, как изменять архитектуру, но что делать, если даже при подборе лучшей архитектуры нас все равно не устраивает результат? Мы можем поработать с данными. Для этого используется аугментация — изменение примеров в наборе данных. Ее можно применять на этапе тренировки и тестирования. 130
Аугментация на этапе тренировки увеличивает набор данных, это особенно актуально для маленьких датасетов. Так же она увеличивает робастность алгоритма к определенным особенностям входа. 131
Что же этот метод из себя представляет? Это сохранение измененных изображений этого же датасета. Изменения могут затрагивать как изменение освещение, так и поворот изображения. Это ограничено только вашим воображением. 131
Аугментация на этапе теста — это генерирование нескольких аугментированных изображений из одного, их предсказание, усреднение всех предсказаний. Усреднение должно быть таким же, как и предсказание изначального изображения. 131
Псевдо - разметка это еще один способ работы с данными. Чаще всего наборы данных размечены не полностью, а лишь частично, причем чаще всего размеченная часть гораздо меньше не размеченной. В таких случаях и помогает псевдо — разметка. Мы обучаем модель по размеченной части набора данных, после чего делаем предсказания на не размеченной части и добавляем то, в чем модель уверенна, в размеченный набор. После чего повторяем. 132
Задачи переноса стиля и поиска изображений по содержанию 133
9. Стаил Трансфер 133
9.1. A Neural Algorithm of Artistic Style 133
Сейчас мы расскажем о переносе стиля. Но что такое стиль? На двух картинах Винсента ван Гога изображено совершенно разное — портрет человека и ночной город. Это называют контентом изображения. Несмотря на это, они чем -то очень схожи. Это «что-то » и называют стилем. Обычно говорят что каждый художник имеет свой стиль. Задача переноса стиля состоит в том, чтобы перенести на изображение определенный стиль, не меняя контент. 133
У задачи переноса стиля есть определенные сложности: 134
Примеров правильной работы нет, поэтому учиться на чем-то готовом не выйдет 134
Понятия похожести стиля и контента размыты,поэтому их необходимо сформулировать с помощью формул для обучения сети 134
Наша мера похожести будет состоять из двух составляющих — мера похожести(сохранности) контента и мера похожести стиля. 134
В качестве меры для контента мы возьмем сумму фиксированных слоев у VGG сети. Считаются выходы слоя для изображения контента и измененного изображения, и расстояние l. Слой можно выбрать какой угодно, но чем он глубже, тем более абстрактные признаки создает. Берется несколько слоев, после чего итоговые значения на каждом слое складываются. 134
Мера для стиля описывается корреляцией признаков сверточной сети, но мы будем считать корреляцию не для всех признаков, а для каждого канала отдельно. 135
Для подсчета корреляции используют матрицу Грамма. В каждой ячейке матрицы будет скалярное произведение каналов. 135
Для итоговой меры стиля считаем расстояние между матрицами Грамма, построенными для выхода слоя, повторяем для нескольких слоев, после чего складываем расстояния с разных слоев. 136
В итоге мы получили формулу для переноса стиля. В ней можно настраивать веса для стиля и контента. Чем больше вес у стиля, тем меньше сохранится контент, и наоборот. 137
9.2. Fast Neural Style 137
Изначальный алгоритм переноса стиля был довольно медленным, поэтому он оптимизировался. В алгоритме Fast Neural Style была оптимизирована нейронная сеть для генерации итогового изображения. В ней применялись Deconvolution слои, которые увеличивали разрешение(например в 2 раза). 137
9.3. Arbitrary-Style-Transfer 137
Fast Neural Style был достаточно быстрым алгоритмом, но в нем для каждого стиля надо было обучать отдельную сеть. В Arbitrary-Style-Transfer улучшили предыдущий алгоритм, немного поменяв подход, что позволило с помощью 1 сети переносить любой стиль. 137
10. CBIR 138
10.1. Поиск изображений по содержанию 138
CBIR — это задача поиска изображений по содержанию. Мы рассмотрим частный случай CBIR – поиск по фото. 138
Для решения задачи будет построена модель, где выходом будет числовой вектор, описывающий изображение. По этим векторам мы и будем сравнивать изображения, и чем больше они совпадают, тем более похожи фотографии. В конце работы модели у нас будет размеченная база данных. Сами признаки записываются в специальную структуру данных для более быстрого поиска похожих признаков. 138
Так как у нас происходит сравнение изображений то очень важным пунктом становится выбор метрики качества. Наиболее популярной метрикой для задачи CBIR является Precision@k. В ней введены два понятия — рекомендованные — наиболее близкие изображения по мнению модели, релевантный — является ли рекомендация объекта правильной. 139
В метрике есть гиперпараметр k, который отвечает за количество близких значений, которые будут участвовать в метрике. Например: на скольки фотографиях из 5 с самым похожим человеком был именно этот человек. Чаще всего k фиксируется, но если нужно, чтобы все фотографии с данным человеком использовались в метрике, это не нужно. 139
10.2. Функции схожести и потерь часть 1 140
Мы разобрались с тем, как будет выглядеть наша система и какие метрики качества нужно использовать, теперь разберемся, как сравнивать признаки друг друга и обучать. В функции схожести и потерь основная цель архитектуры — создать признаки изображения, поэтому мы возьмем архитектуру классификации с обрезанной частью. Цель функции схожести — находить расстояние между описаниями признаков. Для описания признаков чаще всего используют косинусное или евклидово расстояние.(евклидово — разница между признаками, возведенная в квадрат, косинусное — скалярное произведение двух векторов деленное на норму). Дополнительно признаки нормируются на единичную сферу(в евклидовом — всегда, в косинусном — часто). 140
141
Мы хотим, чтобы похожие объекты лежали близко друг к другу, а непохожие далеко. 141
Мы рассмотрим несколько функций, реализующих данный функционал. 141
Контрастная функция потерь: 142
Если признаки принадлежат одной и той же категории, то мы их располагаем рядом, если признаки сильно различаются, то мы максимизируем расстояние между ними, если оно меньше заранее выбранного числа m, в противном случае не трогаем. 142
Триплетная функция потерь похожа на контрастную, но теперь мы располагаем объекты относительно якоря. Здесь так же есть число m, меньше которого расстояние между позитивным и негативным быть не может. 143
Но у обоих этих функций есть недостаток — они могут стать 0 при выборе правильно работающих примеров, из — за чего модель перестает учиться. 144
Для этого триплеты делят на 3 категории: сложные, средние и легкие, после чего доучивают сеть на сложных триплетах. 144
Для разделения триплетов сначала строим признаки для большого батча, после чего для каждого якоря подбираем самый ближний негативный и самый дальний позитивный примеры. На ранних этапах обучения рекомендуется выбирать полусложные теплеты. 144
10.3. Функции схожести и потерь часть 2 145
Альтернатива обучения признаков напрямую — ArcFace – софтмакс классификация. Для нее строится сеть, где добавляется слой, переводящий все лица(если нужно распознавать лица) в отдельные классы, после чего softmax присваевает классам в вероятности. 145
Недостатки метода: 145
Обучение классификации требует набор данных со специальной разметкой. 146
Плохо пригоден для больших наборов данных. В этом случае требует специальной реализации из-за ограничения максимальной памяти GPU. 146
10.4. Ранжирование 146
Ранее мы размечали базу данных с фотографиями. Но как же производить поиск по базе? Обычный перебор слишком долог при большом наборе данных и для нас не подходит. Для этого используют приближенный поиск. 146
Рассмотрим самый популярный алгоритм приближенного поиска — Annoy. 146
У нас есть фото с большим набором точек. Задача — найти ближайшую точку к случайно выбранной. Мы выбираем две случайные точки, проводим линию между ними и разделяем фото на 2 области. Продолжаем процедуру до критерия остановки — недостатка точек для дальнейшего разделения. 146
В итоге у нас получилось бинарное дерево, во которому мы и будем искать соседей! 148
Азы работы с изображениями 4
1. Азы работы с изображениями 4
1.1. Попиксельная обработка изображений 4
1.2. Задача маттинга и морфология 4
1.3. Свертки 4
2. Базовые алгоритмы над изображениями 4
2.1. Интерполяция 4
2.2. Фильтрация 4
2.3. Гистограммы 4
2.4. Практика в python (часть 1/2) 4
2.5. Практика в python (часть 2/2) 4
Границы и признаки 4
3. Границы 5
3.1. Оператор Собеля 5
3.2. Оператор Лапласа 5
3.3. Canny 5
3.4. Поиск карты с помощью canny 5
4. Пирамиды и признаки 5
4.1. Пирамиды 5
4.2. Угловые точки 5
4.3. HoG 5
4.4. SIFT 5
Задача классификации для нейронных сетей 5
5. Задача классификации 5
5.1. Классификация изображений и ImageNet 5
5.2. Базовые слои и оптимизация 5
5.3. FLOPs & FoV 5
6. Архитектуры 5
6.1. VGG & BatchNorm 5
6.2. Модели ResNet 5
6.3. XceptionNet & MobileNet 5
6.4. MNAS 5
6.5. EfficientNet 5
6.6. ViT 5
7. Практическая методология 6
7.1. Что делать если плохо учится? 6
7.2. Аугметация и Псевдо-разметка 6
7.3. Практика. Дообучение и аугметация часть 1 6
7.4. Практика. Дообучение и аугметация часть 2 6
Задачи переноса стиля и поиска изображений по содержанию 6
8. Признаки, обученные сетью 6
8.1. Что учат нейронные сети? часть 1 6
8.2. Что учат нейронные сети? часть 2 6
9. Стаил Трансфер 6
9.1. A Neural Algorithm of Artistic Style 6
9.2. Fast Neural Style 6
9.3. Arbitrary-Style-Transfer 6
10. CBIR 6
10.1. Поиск изображений по содержанию 6
10.2. Функции схожести и потерь часть 1 6
10.3. Функции схожести и потерь часть 2 6
10.4. Ранжирование 6
Детекция объектов 6
11. Введение в детекцию объектов 6
11.1. Детекция объектов 7
11.2. Метрика для задачи детекции 7
11.3. Детектор лиц 7
12. Глубинное обучение для детекции объектов 7
12.1. R-CNN: Regions with CNN features 7
12.2. Fast R-CNN 7
12.3. Faster R-CNN 7
12.4. Одностадийные детекторы 7
12.5. Трансформеры для детекции объектов 7
13. Практика детекции объектов 7
13.1. Детекция объектов с OpenCV 7
Сегментация изображений 7
14. Введение в семантическую сегментацию 7
14.1. Формулировка задачи 7
14.2. Метрика Mean Intersection over Union 7
14.3. Пороговая сегментация 7
15. Сегментация и глубинное обучение 7
15.1. U-Net 7
15.2. Расширенная свертка 7
15.3. Объектная сегментация 7
15.4. Одностадийная инстанс сегментация 7
15.5. Практика. Сегментация 8
16. Обучение метрики 8
16.1. Постановка задачи 8
16.2. Распознавание лиц 8
Азы работы с изображениями
1. Азы работы с изображениями
1.1. Попиксельная обработка изображений

Какой-то вводный слайд
Цель компьютерного зрения (КЗ) - научить компьютер видеть так, как видит человек. Это довольно тяжёлая задача, т.к. для человека видеть - это естественный процесс, а для компьютера - ни разу. Все КЗ строится вокруг обработки изображений (даже в видео, которое состоит из кадров), поэтому важно понять, как они обрабатываются.
Узнаем, как устроено изображение и как его редактировать.
Начнем с черно белых (ч/б) изображений:

Слайд 1
Любое изображение в компьютере – это матрица с числами, каждое число соответствует одному пикселю (пиксель - один кусочек цвета на изображении) Чем больше число, тем светлее пиксель, чем меньше - тем темнее. Все значения, т.е. формат хранения, ограничены. Стандарт: 0 - абсолютно черный цвет, а максимальное значение, которое зависит от обрабатывающей программы, может быть разным, и это абсолютно белый цвет.
Стандартно используется два типа:
Первый - float - 0 черный, 1 - белый, между - оттенки серого (используются в промежуточных вычислениях внутри алгоритма)
Второй - ubyte - максимально эффективный по памяти - используется для хранения изображений. С виду может показаться, что 256 значений для цвета это не очень много, но человеческому глазу этого достаточно.
Мы поняли, как устроено изображение, время попробовать его обработать:

Слайд 2
Самое простое, что можно сделать, это прибавить ко всем пикселям константу.
Важно сделать замечание, что при прибавлении числа к пикселю мы можем выйти за 1, в таком случае надо обрубить это значение, чтобы оно стало равно 1.
Что мы видим - изображение просто становится более белым (ярким) – чем выше значение пикселя, тем он ярче.



Слайд 3 – сразу 3 фотки
Аналогично мы можем вычесть константу, при этом тоже важно следить, чтобы значение пикселя не вышло в отрицательное значение, а изображение становится темнее. Также можно умножить или разделить пиксель на значение.

Слайд 4
Описанные операции называются попиксельными, потому что применяются к каждому пикселю независимо. Мы рассмотрели самые тривиальные из них, но они могут быть какими угодно. Для визуализации используются кривые. В качестве примера мы рассмотрим гамма коррекцию. Гамма коррекция была придумана для того, чтобы регулировать яркость изображений и используется в телевизорах – из за того, что все экраны разные, для того, чтобы картинка смотрелась одинаково, нужно применять предобработку.
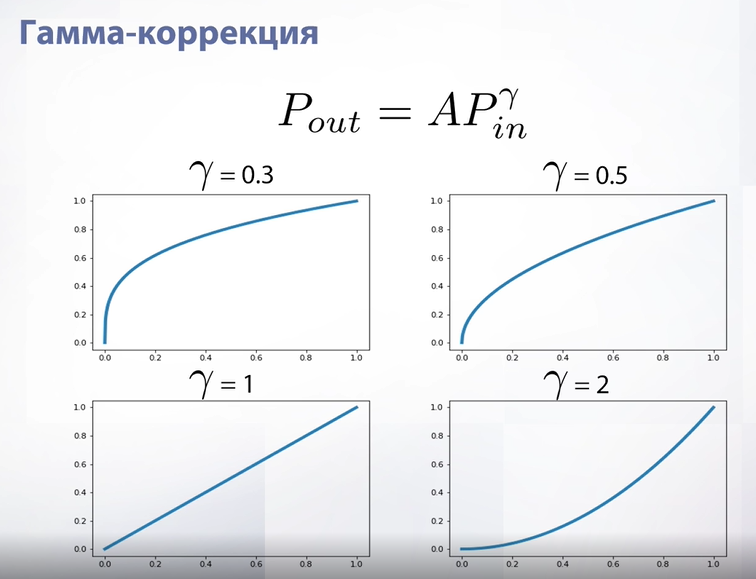
Слайд 5
Гамма коррекция – это просто степенная функция. А - нормализационный коэффициент – нужен, если формат хранения пикселей не лежит во флотах. Если же формат хранения от 0 до 1, то мы просто возводим пиксель в степень.
Если параметр «гамма» единица – то кривая становится просто прямой и изображение после применения данной функции не меняется. В иных случаях она становится немного вогнутой.
По осям нарисованы исходные значения пикселя и значения после применения функции.

Слайд 6
Посмотрим, как выглядит гамма коррекция на примере. Если «гамма» меньше 1, то изображение становится светлее, если больше 1 – темнее.


Слайд 7 – 2 картинки
Теперь время перейти к цвету. Самый классический способ хранить цветные изображения – это RGB формат. Этот формат получил свое название из-за того, что в нем хранится 3 цвета – синий, зеленый и красный. Например, в мониторах каждый пиксель состоит из 3-х субпикселей, которые при смешивании могут дать около 16,7 миллионов цветов.

Слайд 8
С этими изображениями можно поиграться точно так же. Например, посмотреть, как ведет себя изображение, если к какому-то из каналов RGB добавить константу. Если добавить константу к красному каналу, то изображение станет более красным, если вычесть – более зелено-синим. Аналогичный результат мы увидим и с другими каналами.
Слайд 9
Мы можем применять нетривиальные функции и к цветным изображениям. Например, уже известную нам гамма коррекцию, только теперь будем применять ее к каждому пикселю в каждом канале отдельно.

Слайд 10
При «гамме» больше 1 мы затемнили изображение, при «гамме» меньше 1 наоборот засветлили. При «гамме» же равной 1 – изображение осталось таким же.
Слайд 11
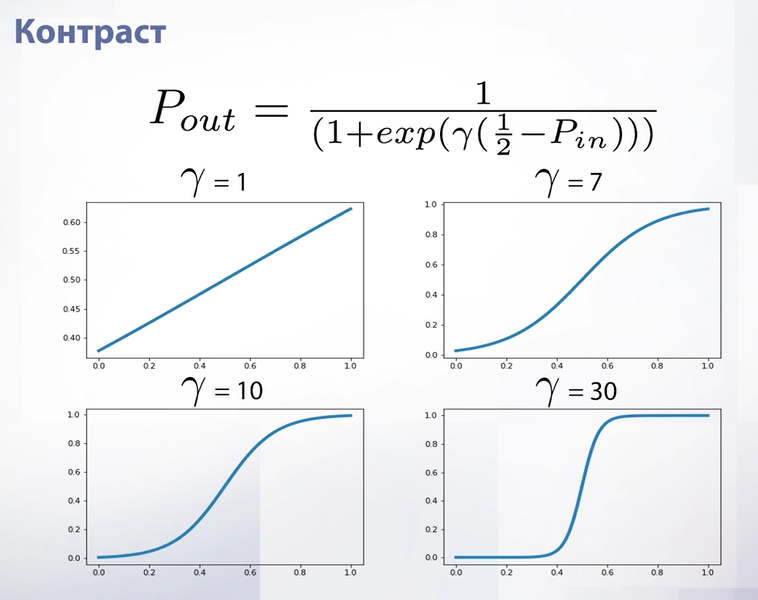
Гамма коррекция не единственная функция, которую мы можем применить к изображению. Например, существует функция контраста. Важная особенность этой функции в том, что при всех параметрах у нас нет ни одного значения функции, при котором изображение было бы таким же, как исходное.

Слайд 12
Рассмотрим контраст на примере. При гамме равной 1 изображение становится более серым, а при росте этого параметра – более ярким, контрастным.
Такие попиксельные операции используются для построения различных крутилок в фоторедакторах. Но если мы хотим построить такую крутилку, нам хотелось бы, чтобы какой-то параметр отвечал за то, чтобы ничего не делать.

Слайд 13
У, например, контраста такого параметра нет. Поэтому прибегают к смешиванию изображений. Смешивание изображений – просто среднее между двумя изображениями. Мы берем первое изображение, берем второе изображение и просто подбираем коэффициент от 0 до 1 и взвешиваем с ним первое изображение и с (1-alpha) второе изображение. Таким образом можно построить крутилку. Первое изображение будет исходным, а второе – примененный на максимум контраст. Все промежуточные значения мы будем регулировать параметром смешивания вместо того, чтобы регулировать параметры контраста. Такой подход можно применять для любых функций.

Слайд 14
Как перевести из цветного изображения в серое? В целом, можно взять один из каналов, но тогда мы просто посмотрим яркость, например, красного и забудем про синий с зеленым. Можно усреднить, но усреднение даст не очень естественную для глаза картинку. Поэтому существуют волшебные константы, которыми взвешивается наше усреднение. Можно заметить, что самый большой цвет тут у зеленого. Это связано с тем, что человеческий глаз наиболее восприимчив именно к зеленому каналу. Поэтому итоговое изображение получается более приятным для глаза.

Слайд 15
Какие еще форматы существуют для хранения цветных изображений? Представим формат RGB в качестве куба. Его верхняя видимая грань – абсолютно белого цвета, противоположная нижняя – абсолютно черного цвета. На его границах есть красный, синий, зеленый цвет – как основные, желтый – как смесь красного с зеленым, фиолетовый – как смесь красного и синего и так далее. То есть наш RGB формат можно визуализировать с помощью куба.
Слайд 16
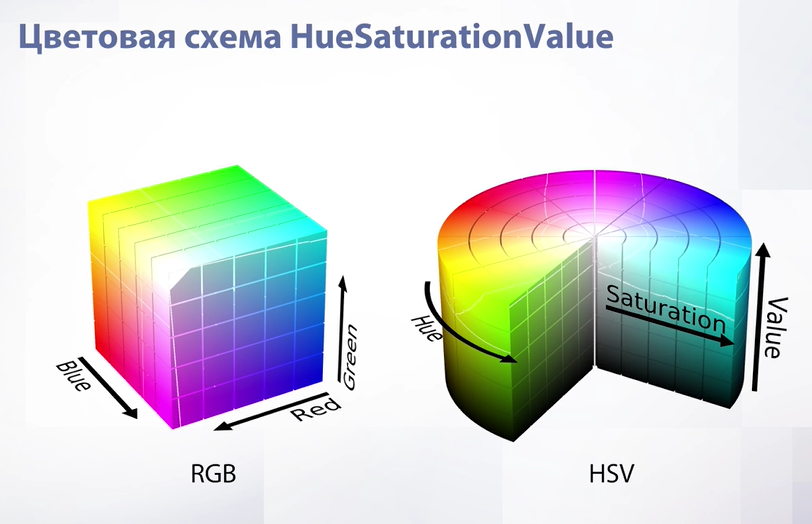
Теперь рассмотрим HSV-схему. Он визуализируется с помощью цилиндра. Зачем HSV в целом нужен? Он нужен для того, чтобы изображения было проще обрабатывать. Все параметры – Hue, Saturation, Value – очень естественны. Что значит естественны? Посмотрим на примере, просто меняя их.

Слайд 17
Hue – это угол поворота в цилиндре. Если не менять угол поворота или изменить его на 2Pi, что является полным оборотом по окружности, то изображение не изменится. Если же крутить на какой-то угол – цвета начинают меняться – желтый переходит в зеленый, синий переходит в красный и так далее.

Слайд 18
Следующий параметр – Saturation. Он меняется домножением. Это расстояние от пикселя в цилиндре до оси цилиндра. На оси пиксель будет абсолютно серым, а чем дальше от оси, тем более насыщенным.

Слайд 19
Параметр Value – это расстояние пикселя в цилиндре до пола цилиндра. Внизу у нас круг абсолютно черного цвета. От этого параметра зависит освещенность изображения.
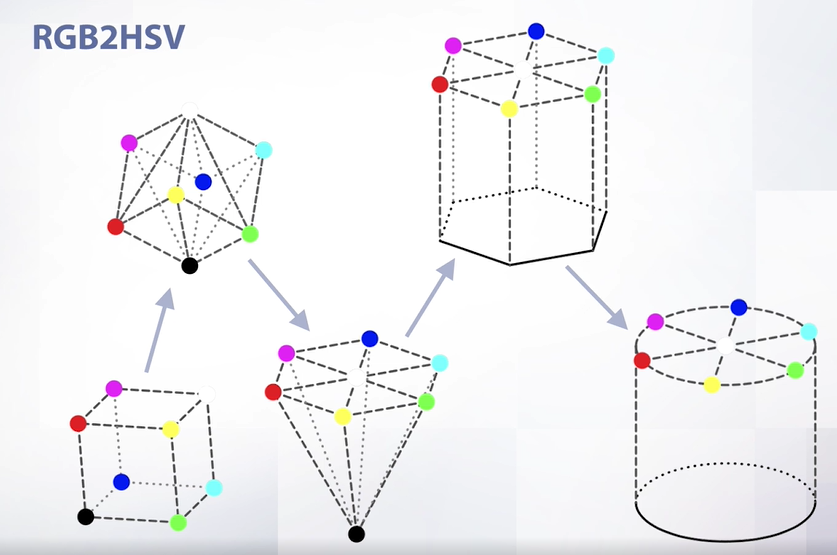
Слайд 20
Перейдем из RGB формата в HSV формат. RGB был кубом, на краях которого были абсолютные цвета. Сначала мы ставим куб на черный цвет. После вытягиваем все цвета, кроме черного, на одну плоскость. После размазываем черный цвет на всю плоскость и сглаживаем.

Слайд 21
RGB и HSV далеко не единственные цветовые схемы, которые можно использовать, хоть они и достаточно популярны. Большая часть форматов развивалась с развитием техники, например с развитием телевизоров и принтеров, и все форматы создавались под нужды определенного устройства, поэтому нужно выбирать цветовую схему в зависимости от поставленной задачи.
1.2. Задача маттинга и морфология

Слайд 22
Время на реальном примере попробовать приобретенные навыки. Рассмотрим задачу Маттинга. Она формулируется довольно абстрактно – у нас есть изображение, на котором есть какой-то основной объект и фон. Нам необходимо построить маску, которая отражала бы, где на изображении находится этот основной объект. Сразу же можно обратить внимание, что маска не абсолютно-белого цвета – у нас имеются промежуточные значения в волосах, т.к. волосы принадлежат одновременно и объекту, и фону. Задача Маттинга как раз и решает проблему поиска маски.
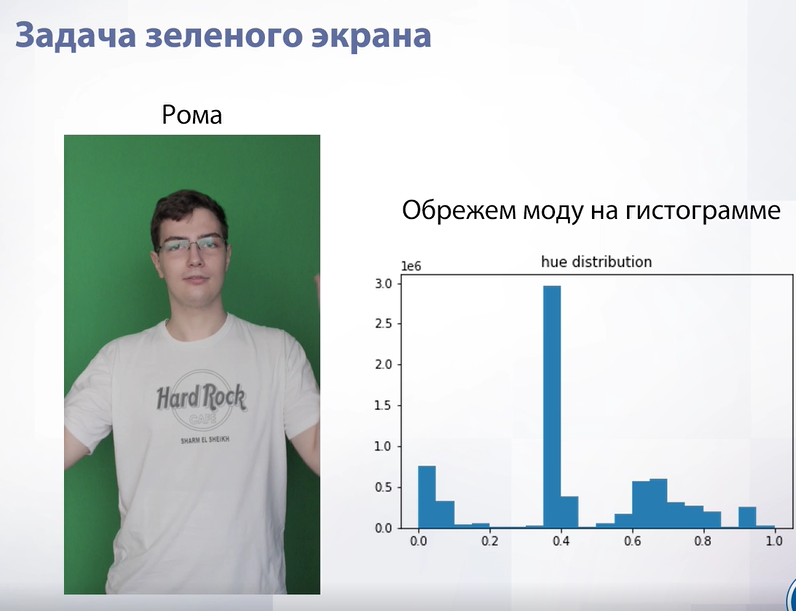
Слайд 23
Рассмотрим более тривиальный случай задачи Маттинга – задачу зеленого экрана. Мы попробуем построить какой-то алгоритм, который не будет идеальным, но будет работать. Наша задача – взять из изображения и выделить все пиксели, где цвет зеленый. Для этого построим гистограмму Hue-значений в HSV формате. Мы увидим, что на гистограмме будет огромный всплеск среди значений. Этот всплеск как раз и относится к зеленому цвету. Если его обрезать, то мы получим:

Слайд 24
Все пиксели, где Hue меньше определенного и больше определенного значений это человек, а между ними – зеленый цвет. Мы получили маску. Она сделала то, что нужно – выделила человека, но в ней есть куча дыр. Эти дыру нужно как-то исправить и тут нам на помощь приходит морфология:

Слайд 25
Морфология – это работа с бинарными изображениями. Бинарное изображение – такое изображение, где есть только 2 значения 0 или 1. Наша маска являлась бинарным изображением – пиксель либо принадлежал диапазону, либо нет. Бинарные изображения практически никогда не используются для реального отображения чего-либо, а используются в промежуточных вычислениях, как раз для таких моментов, когда в алгоритме возникает задача профильтровать пиксели по какому-нибудь критерию.

Слайд 26
Первая операция – это эрозия. Эрозия формирует из одного изображения новое, записывая в значения пикселя в новом изображении минимум из значений соседей этого же пикселя на предыдущем изображении. Сосед – это параметр, например в текущем примере это тот, кто граничит ребром.

Слайд 27
Применим эрозию на реальной картинке. Видно, что наша буква уменьшилась. Отсюда и названия эрозии – если наш объект белый, то эрозия его сожмет.
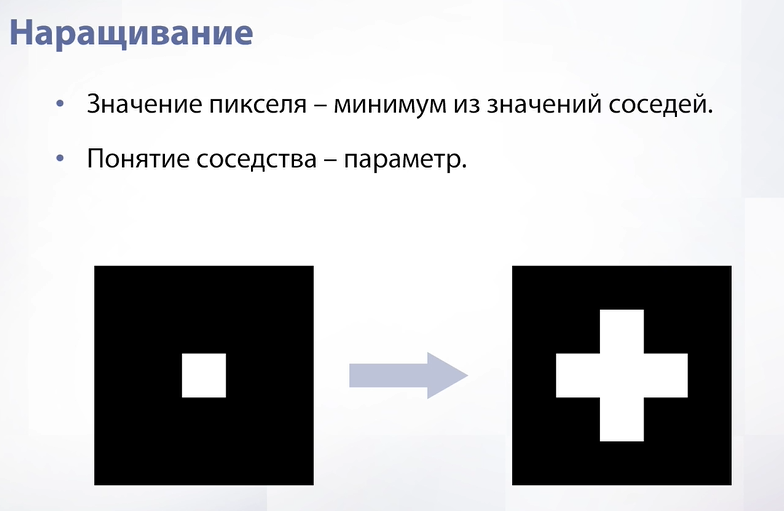
Слайд 28
Следующая операция аналогична и называется наращиванием. Теперь мы берем не минимум, а максимум. В этом случае расширяются не черные области, а белые.
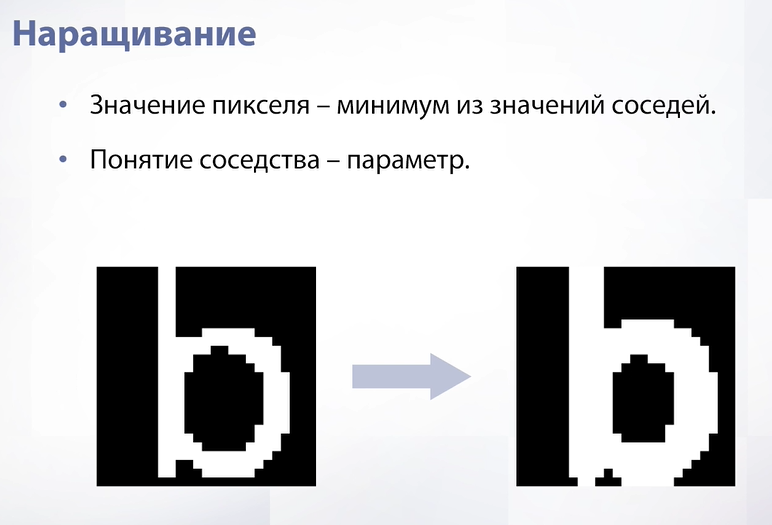
Слайд 29
На примере той же буквы мы видим, что наращивание называется наращиванием, потому что если наш объект белый, то применение этой операции его увеличит.
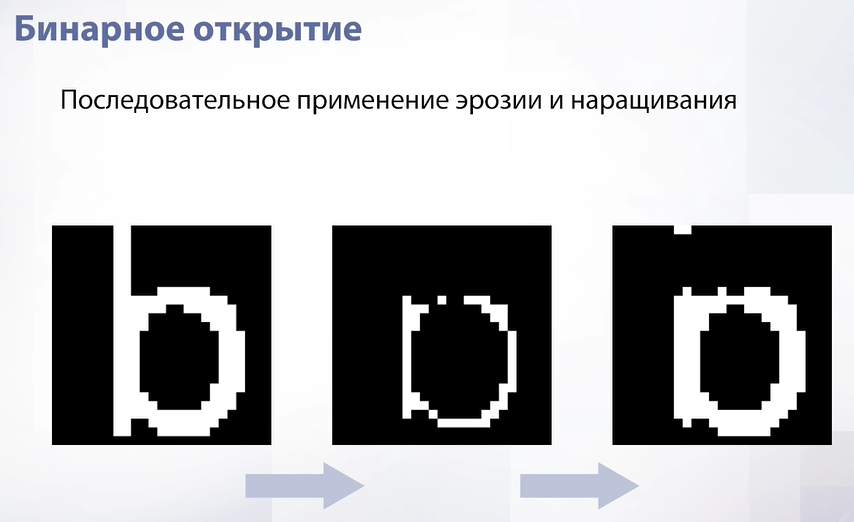
Слайд 30
Теперь рассмотрим более сложную операцию – бинарное открытие. Это просто последовательное применение двух операций – эрозии и наращивания. Вначале мы уменьшим изображение, а затем увеличим. В результате мы удалим тонкие элементы на изображении. Например, в данном случае удалилась палка буквы.

Слайд 31
Аналогичная операция – бинарное закрытие, только теперь мы сначала применяем наращивание, а потом эрозию. Это нужно, чтобы закрыть черные дыры.
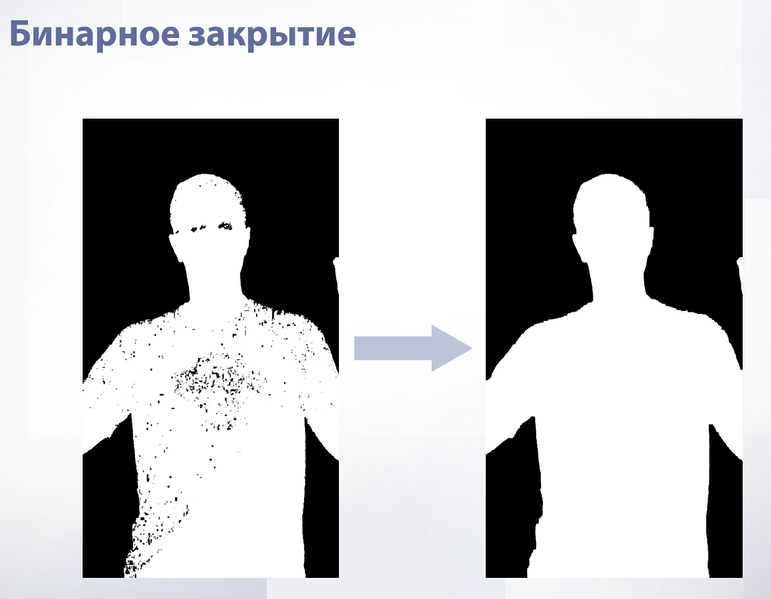
Слайд 32
Эта именно та операция, которая нам нужна. Если применить бинарное закрытие к той маске, которую мы получили, то уйдут все дыры.

Слайд 33
Теперь поговорим про RGBA. А – отвечает за альфа канал, то есть за прозрачность. В целом его можно добавить не только к цветовой схеме RGB, а вообще к любой и таким образом хранить информацию, где на изображении находится фон, а где находится объект. По зеленому экрану мы нашли, где находится человек, а где фон. Мы можем записать человека в альфа канал, таким образом добавив прозрачности к нашему изображению. Что у нас получится в итоге?

Слайд 34
В итоге у нас получится изображение без фона. В целом альфа канал можно использовать и для смешивания изображений, например взять и заменить фон, что часто используется для монтажа видео.
1.3. Свертки
До этого момента мы говорили в основном о попиксельных операциях – операциях, которые используют только один пиксель и как-то его изменяют. Теперь время начать использовать в наших функциях сразу несколько пикселей.
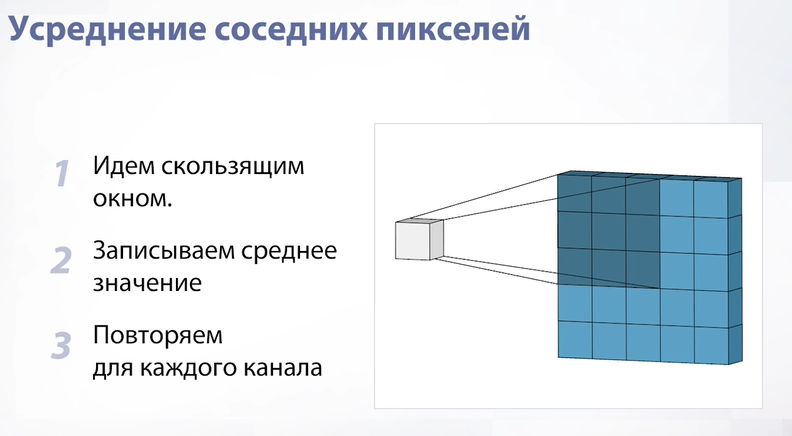
Слайд 35
Начнем с самого простого – будем идти по нашему изображению окошком и записывать в пиксель нового изображения среднее значение из пикселей в нашем окошке. Для цветных изображений мы делаем то же самое, но для каждого канала независимо. Давайте посмотрим на результат:


Слайд 36
Для черно белого изображения – изображение стало более мутным. Для цветных то же самое – цвет не потерялся, но качество изображения ухудшилось. Давайте более внимательно посмотрим на объекты вблизи:

Слайд 37
Если присмотреться к объекту, у которого очень четкие границы, то можно заметить артефакты. Конкретно здесь артефакт называется «звенящим артефактом». Он заключается в том, что четкие границы объекта размазываются и становятся повторяющимися и «призрачными». Если мы хотим добиться размытия изображения, то это точно не тот эффект, который нам нужен. Появляются артефакты буквально из-за усреднения, т.к. мы усредняем все пиксели с одинаковыми весами в независимости от того, на каком расстоянии они находятся от центрального. Решением проблемы такого артефакта будет усреднение тем же окном, но взвешенно.
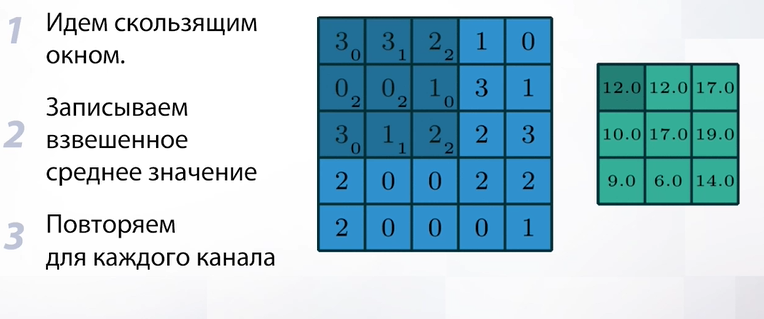
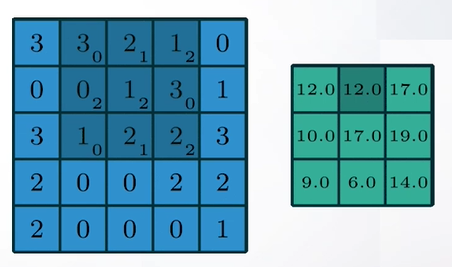
Слайд 38
Такое взвешенное усреднение называется сверткой. Свертка - это такая же операция, где мы идем скользящим окном, но теперь мы записываем не просто среднее значение, а взвешенное среднее значение с какими-то весами и делаем так для каждого канала независимо. Но какие веса нам надо выбрать, если мы хотим замылить наше изображение и при этом не породить артефакты.

Слайд 39
Классическим выбором является фильтр гаусса. Мы чуть позже разберем, что это такое, а пока просто посмотрим на то, как он работает. На слайде мы видим, что изображение стало более мутным, но при этом артефактов не возникло и можно хорошо разглядеть объект.

Слайд 40
Что же такое фильтр гаусса? Идея в том, чтобы взять двумерное гауссовское распределение – это такой купол, где есть мода, значение распределения в которой максимально и этот купол очень быстро уходит вниз и чем дальше мы находимся от моды, тем ближе к нулю веса пикселей.

Слайд 41
Если нарисовать гауссовское распределение, то мы получим следующий белый размытый кружок.

Слайд 42
Проблема гауссовского распределения в том, что в теории оно бесконечно и если мы захотим усреднять наши пиксели именно с ним, то нам придется для каждого пикселя усреднять всю картинку. Но за счет того, что гауссовское распределение очень быстро убывает и через какой-то момент времени становится очень близким к нулю мы можем брать окно размером 6 сигма, потому что после него значения настолько незначительны, что практически не влияют на итог. На примере гауссовский фильтр размером 3 на 3, т.е. сигма здесь ½.

Слайд 43
Собственно, мы берем наше изображение, применяем к нему гауссовский фильтр и получаем результат, который мы видели несколько слайдов назад.

Слайд 44
Свертки используются очень и очень часто – это одна из самых ключевых операций в компьютерном зрении, которая применяется практически везде и делает очень много всяких полезных штук. Например, свертки могут показать нам границы, т.е. те места, в которых объекты меняются (один объект сменяет другой). Зачем и как искать границы мы разберем чуть позже, а пока на слайде показан пример работы сверток в выделении границ.


Слайд 45
Также свертки могут применяться для стилизации изображений, как, например, контрастность в попиксельных операциях, или же применяться для размытия изображений, как во время движения руки при записи видео на камеру. Зачем это вообще нужно? Такое бывает полезно, когда мы учим какой-то алгоритм (нейронную сеть) и хотим, чтобы она училась работать на таких изображениях. Мы берем нормальное изображение, каким-то образом портим его и получаем уже несколько изображений для обучения нейронных сетей. Такой метод называется аугментацией, но подробнее об этом мы поговорим позже.
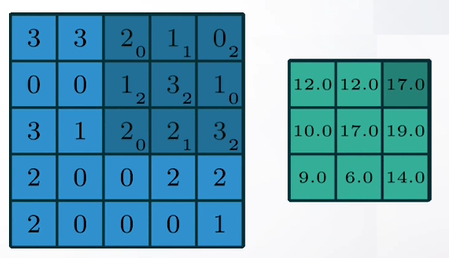
Слайд 46
Настало время поговорить о свойствах сверток. Самое очевидное из них – то, что они уменьшают размер изображения. Почему так происходит? Потому что мест, куда мы можем приложить наше ядро свертки (окно, по которому мы идем по изображению) просто меньше, чем количество пикселей. Соответственно, наше итоговое изображение немного уменьшается.

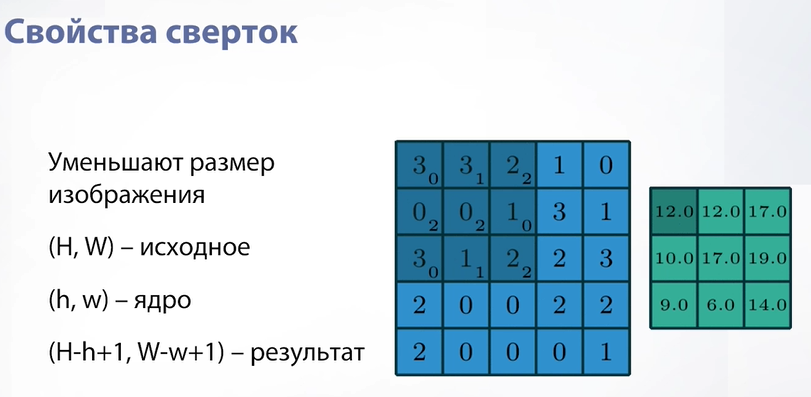
Слайд 47
Если мы хотим избежать этого эффекта, т.е. хотим, чтобы наша свертка была такого же размера, как исходное изображение, мы можем воспользоваться паддингом. Паддинг – это просто обивка нашего изображения временными пикселями, которые нужны для того, чтобы количество мест, в которые мы можем приложить свертку, увеличилось и уменьшение изображения съело бы пиксели паддинга, но оставило оригинальные. Паддингов бывает много типов. Самый простой – это константный, когда мы просто взяли и обили наше изображение временными пикселями. Конкретно этот вариант часто применяется в нейронных сетях. Самый продвинутый вариант – симметричный. Тут мы отражаем нашу картинку вдоль оси, которую мы хоти обить.
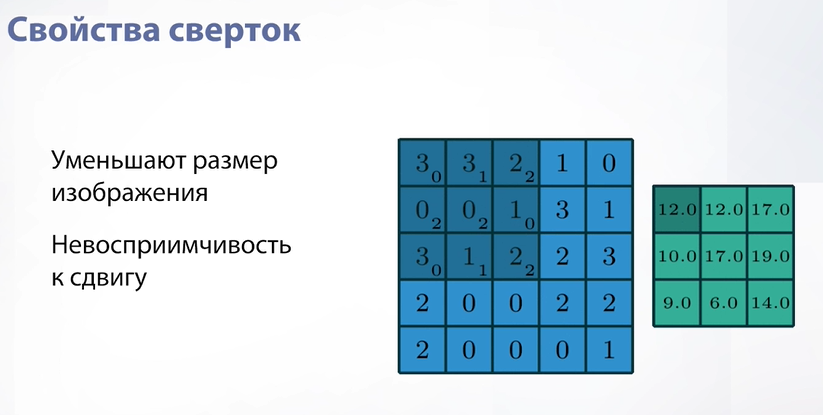
Слайд 48
Следующее свойство сверток – невосприимчивость к сдвигу. Это свойство будет важно, когда мы будем говорить о нейронных сетях, но понять его можно уже сейчас. Что это значит? Это значит, что где бы не находился объект на нашем изображении свертка обработает его одинаково. Будь он в левом углу или в правом. Потому что мы идем скользящим средним и применяем его в независимости от того, где мы находимся.
Слайд 49
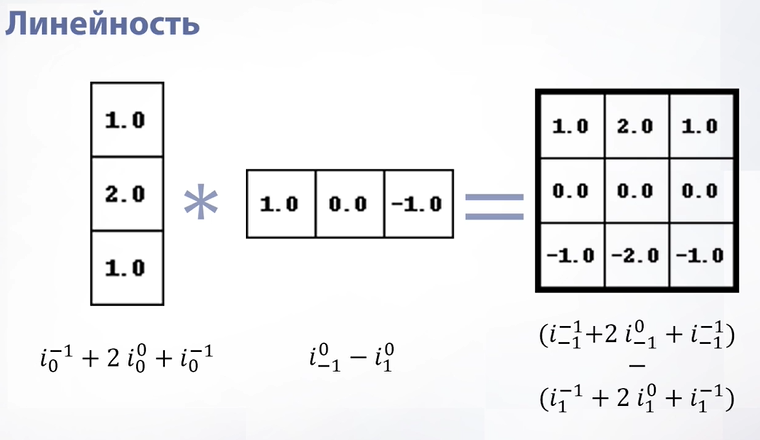
Еще одно свойство – комбинация сверток – свертка. Почему так? Свертка – это линейная операция, а комбинация двух линейных операций тоже линейна, соответственно, комбинация двух сверток тоже свертка. Давайте рассмотрим это на примере. У нас есть два ядра сверток – одно вертикальное, другое горизонтальное. Мы можем записать их как формулы. В формулах нижний индекс это движение по горизонтали, верхний – движение по вертикали. Соответственно, мы можем записать новую формулу, которая будет последовательным применением двух наших формул. В итоге мы снова получим какую-то формулу, в которой опять будет линейная операция и эта линейная операция будет в окне, просто чуть большего размера. Эту линейную операцию мы сможем записать как свертку.
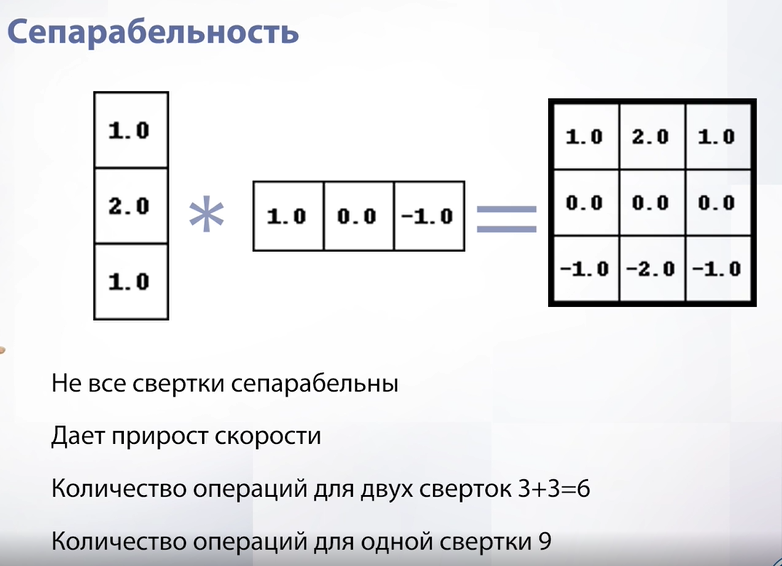
Слайд 50
Из линейности вытекает еще одно свойство, которое доступно не всем сверткам, а именно сепарабельность. Сепарабельность – возможность разложить нашу свертку на какие-нибудь две. В нашем примере итоговая свертка сепарабельна, потому что она раскладывается на две независимые свертки, одна из которых горизонтальна, а другая вертикальна. Зачем это нужно? Это нужно для прироста скорости. Давайте посчитаем конкретно на этом примере. Если мы применим итоговую свертку, то мы применим 9 операций (9 весов), а если мы применим вертикальную и горизонтальную, то мы сделаем всего 6 операций. Это может стать важным на масштабе сверток – допустим у нас свертка не 3 на 3, а 9 на 9, тогда мы сделаем 18 операций против 81.

Слайд 51
Вот мы и поговорили о свертках. Поняли, где они могут применяться и что могут делать сами по себе. Давайте попробуем сделать с ними что-то интересное и полезное. Для этого посмотрим на портретную съемку. Портретная съемка делается с помощью профессиональных камер, на которую в результате съемки человека получается красиво размытый задний фон (эффект Боке).

Слайд 52
Эффект Боке доступен далеко не для всех камер. На самом деле для профессиональной съемки покупаются специальные камеры, заточенные на то, чтобы снимать людей с определенного расстояния и в итоге получать красивое размытие. На слайде пример фотографии одного и того же объекта, но на разные камеры. У одного присутствует эффект Боке, у другого нет, потому что это буквально физическое свойство камеры. Большая часть камер сейчас – камеры мобильных телефонов. В них эффект Боке недоступен и, скорее всего, никогда не будет доступен, потому что это физическое свойство камеры, которое требует, чтобы камера была большой, а в телефоне физически нет места для такой. Остается только имитировать этот эффект.

Слайд 53
Как мы будем это делать? Мы найдем человека на изображении так же, как мы делали для зеленого экрана, но в этом случае воспользуемся каким-то готовым решением и предположим, что у нас уже есть готовая маска. Вторым шагом мы размоем наше исходное изображение, таким образом размыв человека и фон. Затем подставим в наше оригинальное изображение размытый фон и таким образом сэмитируем эффект Боке.






Слайд 54
Вот фотография. Мы вытаскиваем маску, после чего удаляем фон (это будет та часть картинки, которая не изменится. Затем размываем наше изображение и инвинтируем маску. Теперь наоборот вырежем человека и оставим фон. После просто сопоставляем. В итоге мы с имитировали сложное физическое свойство камеры просто используя алгоритмы.
2. Базовые алгоритмы над изображениями
2.1. Интерполяция
Поговорим про интерполяцию. Интерполяция нужна для изменения геометрии изображения. Что же это значит? Сейчас узнаем:
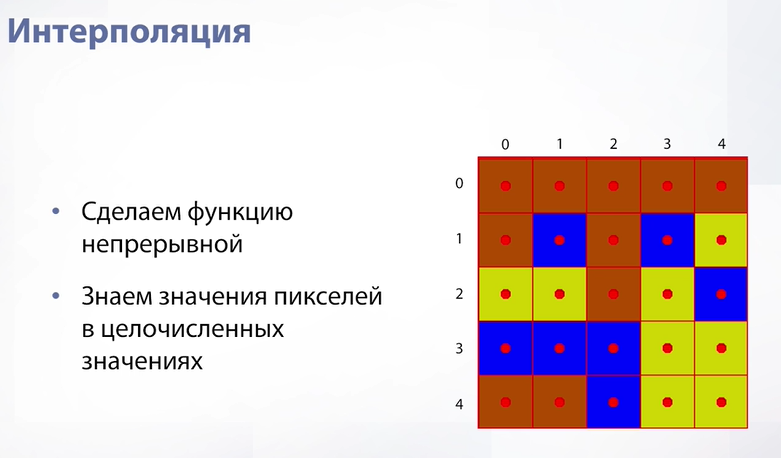
Слайд 55
Давайте посмотрим на наше изображение как на функцию. Функция получается дискретная. В целочисленных значениях мы можем знать значение пикселя. Но что если мы захотим узнать значения между пикселями, т.е. сделать нашу функцию непрерывной. Если мы делаем нашу функцию непрерывной, то тогда мы будем точно знать значения в очень конкретных местах (в серединах нашего пикселя). Там мы гарантированно даем ответ – просто из нашей дискретной функции вытаскиваем его. Но как нам ответить на вопрос «что находится между ними?» Самый простой способ – это метод ближайшего соседа. Метод ближайшего соседа в том, что мы для нашего нецелочисленного значения находим ближайшее целочисленное значение и говорим, что значение здесь соответствует значению в ближайшем целочисленном. Наша картинка от этого вообще не меняется и фактически получается ровно то отображение, которое было изначально.

Слайд 56
Давайте теперь в таких формулировках попробуем изменить размер нашего изображения. То есть, как например на слайде, мы из изображения 5 на 5 попробуем сделать изображение 7 на 7. Значит нам нужно как-то заполнить наши новые пиксели в разрешении 7 на 7:
Слайд 57
Что нужно сделать для этого? Нужно взять координатную сетку изображения 7 на 7 и наложить на исходное изображение. Получим новую сеточку:

Слайд 58
Давайте в новой сетке расставим точки аналогичные тем, которые мы расставляли, когда говорили про интерполяцию. Это будут те точки, в которых нам необходимо узнать значение, чтобы сделать наш оверсайз (увеличение разрешения). Эти точки находятся далеко не в центрах исходного изображения. Соответственно нам нужно понять какое значение в них записывать. Важное замечание перед тем, как мы начнем использовать уже нам знакомый метод ближайшего соседа это то, что чтобы воспользоваться методом ближайшего соседа (и вообще любой интерполяцией) нам необходимо сопоставить координаты исходного изображения с координатами нового изображения. Для этого мы должны сопоставить их углы. Углы будут находится в -1/2 и -1/2. Так происходит потому что т.к. наше изображение было дискретной функцией, точка 0 0 отвечала за центр пикселя, в то время как угол находится немножко выше и левее и там будет точка -1/2 -1/2 и совмещать мы должны конкретно по этой точке.
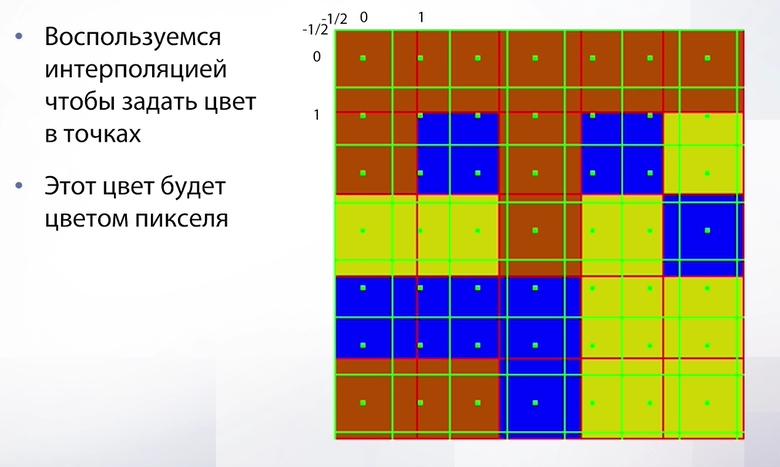
Слайд 59
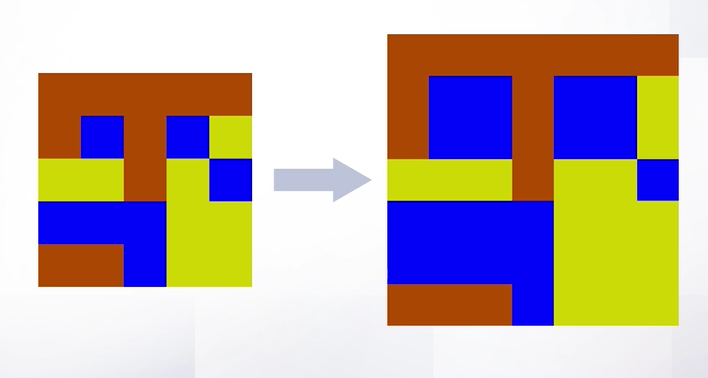
Теперь, когда мы разобрали такой технический момент, мы можем воспользоваться интерполяцией – просто взять, найти ближайшую целочисленную точку и из нее вытащить значение. Вот что получится:
Слайд 60
В целом, получилось неплохо. Но, как можно заметить, изображение изменилось, изменились пропорции. Конечно же можно сделать и лучше.

Слайд 61
Лучше можно сделать с помощью билинейной интерполяции. Идея в том, чтобы вытаскивать значения не из одного пикселя, а усреднять из соседних пикселей. Как работает билинейная интерполяция? Для начала рассмотрим одномерный случай, т.е. линейную интерполяцию, когда у нас функция одномерная (просто прямая). В данном случае мы, чтобы найти значение в новой точке, берем значения в ее соседях и усредняем пропорционально расстоянию до этого соседа (т.е. чем расстояние больше, тем вес у цвета меньше).

Слайд 62
Перенесем эту идею на двумерный случай (для картинок). Получим билинейную интерполяцию. На самом деле билинейная интерполяция – это просто 3 линейных интерполяции. Мы берем нашу точку, находим 4 соседних пикселя, в начале усредняем одну пару из них, потом вторую и затем усредняем наши усреднения. Итого 3 операции.

Слайд 63
Итак, что мы будем делать? Мы будем находить координату желаемого пикселя и считать его значение по четырем соседям. Здесь есть одна проблема – в пикселях, которые находятся на краях, потому что для них может не найтись 4 соседей. Например, для левого верхнего угла у нас вообще будет только один сосед, т.к. в округе только один пиксель. Что нужно сделать в таком случае?
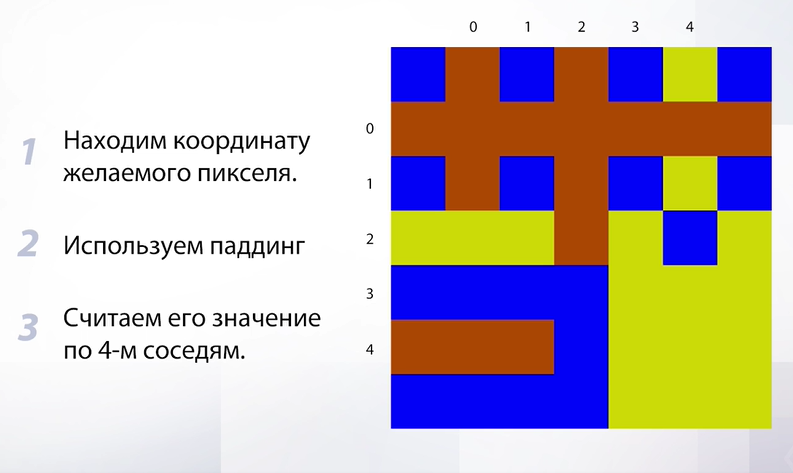
Слайд 64
Воспользоваться уже знакомым нам паддингом – обить наше изображение временными пикселями которые мы будем использовать для усреднения в тех местах, где есть недостаток в соседях. Теперь у нас все готова для применения билинейной интерполяции, посмотрим на результат:

Слайд 65
Получилось вот такое изображение. Здесь уже получше с пропорциями, лучше угадывается какое изображение было исходным. В целом, билинейная интерполяция - это классический выбор, когда мы пишем алгоритмы. Чаще всего применяется она, но справедливости ради нужно упомянуть об артефактах:
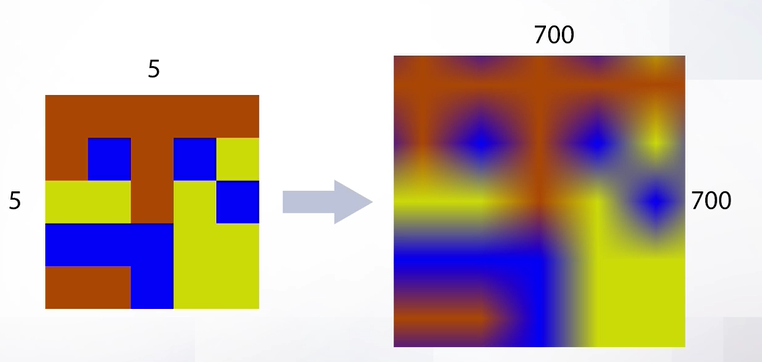
Слайд 66
Артефакты возникают, когда мы очень сильно хотим увеличить разрешение, например с 5 на 5 до 700 на 700. В этом случае мы получим артефакты в виде звездочки. Скорее всего, такого сильного увеличения разрешения не потребуется в обычных задачах, но можно применить и бикубическую интерполяцию, которая поможет избавиться от артефактов. А пока давайте сделаем небольшой вывод про билинейную интерполяцию – она работает быстро (здесь присутствует всего 3 операции и за счет этого она используется чаще всего). Этот алгоритм чаще всего используется в промежуточных вычислениях и в целом применяется чаще всего. Но так что за бикубическая интерполяция?
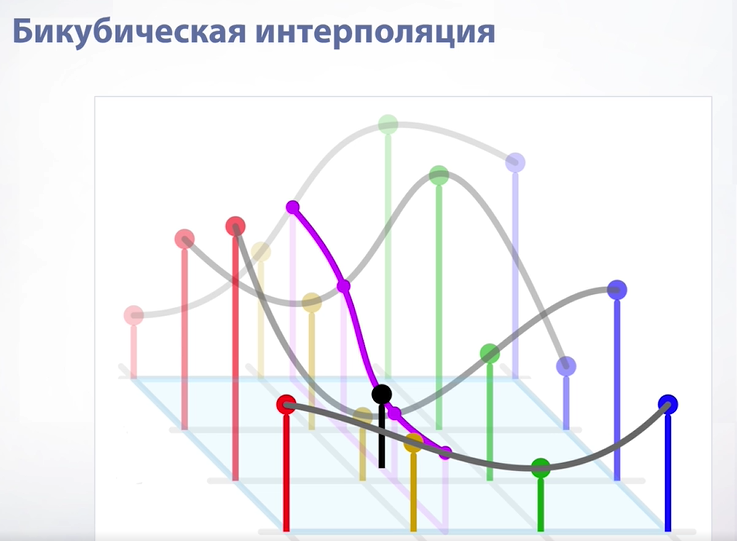
Слайд 67
Мы не будем подробно разбирать бикубическую интерполяцию, скажем только, что делается она за счет последовательного применения сплайнов. Важно обратить внимание на количество операций, которое здесь требуется – вначале мы строим 4 сплайна по 4 точкам, затем по ним строится финальный сплайн, откуда берется итоговое значение. В сравнении с билинейной интерполяцией это очень долгий процесс и поэтому бикубическую интерполяцию практически не используют в алгоритмах.
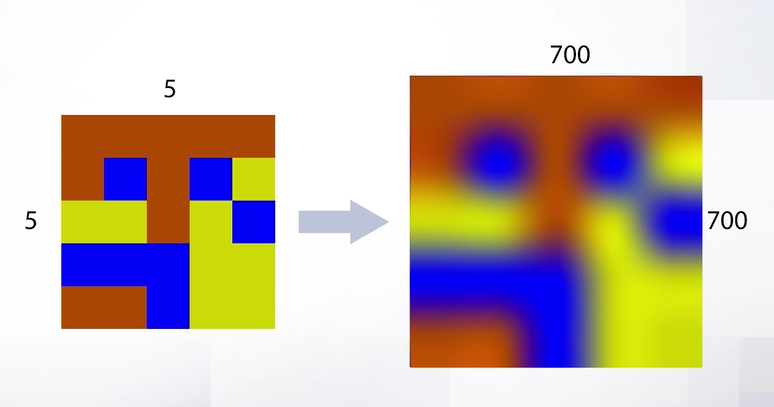
Слайд 68
В результате применения бикубической интерполяции к сильному увеличению разрешения мы сможем избавиться от артефактов в виде звездочек. Если делать небольшой вывод по такой интерполяции, то можно отметить, что она практически не используется в алгоритмах, а применяется только в фоторедакторах, где важно сохранить максимальное качество в ущерб скорости.

Слайд 69
Теперь поговорим об уменьшении разрешения. Самый простой способ как мы можем это сделать – это взять нашу сетку на новом изображении, подставить ее в старое изображение и по координатам нужной интерполяции вытащить значения. Получается что-то такое:


Слайд 70
Если присмотреться, то можно заметить, что появились артефакты. Такие артефакты называются алиасингом (очень резкие переходы). Они возникают из-за того, что далеко не все пиксели участвуют в интерполяции, т.е. мы можем спокойно с таким подходом окно 5 на 5 перевести в 1 пиксель и при этом воспользоваться только 4 пикселями и потерять кучу информации, в результате чего переходы становятся очень резкими. Как решить эту проблему? Нам нужно сглаживать изображение до понижения разрешения, т.е. мы будем понижать теми же шагами, но перед тем, как вытаскивать координаты на старом изображении мы сгладим наше старое изображение, т.е. пройдем фильтром гаусса и получим замыленное изображение:

Слайд 71
В итоге артефакты уходят. В целом, чтобы артефакты ушли, можно делать сглаживание и после интерполяции, но в таком случае мы получим слишком замыленное изображение, а если сделать до, то мы уберем артефакты и оставим нормальное разрешение. Такая дополнительная операция называется анти-алиасингом.

Слайд 72
Еще раз посмотрим на разницу если мы делаем размытие и если не делаем. Что мы можем сделать с изображением еще?


Слайд 73
Мы можем поворачивать изображения. Казалось бы, причем тут интерполяция, но повернутое изображение на самом деле выглядит как картинка с черными рамками, просто все черное здесь имеет в альфа канале полную прозрачность. Если задуматься, то можно понять, что при повороте у нас не будет однозначного соответствия между пикселями – пиксели попадут в промежутки между целочисленными значениями и их придется как-то приближать.

Слайд 74
Еще можно делать аффинные преобразования, т.е. изменять геометрию изображения.

Слайд 75
Для всех этих применений интерполяции схема примерно одинаковая. Мы для каждого пикселя на генерируемой картинке будем находить координаты этого пикселя на исходной. Важно, что именно в таком порядке – что мы будем искать координаты новых пикселей на исходной картинке, потому что иначе мы не закроем все дыры. Затем мы считаем значение интерполяции.
2.2. Фильтрация
Время поговорить про фильтрацию. Фильтрация нужна, когда изображения зашумлены, например, из за особенностей камеры или из за неправильной работы алгоритмов (как, например, при понижении размерности при интерполяции). Какие существую естественные шумы?

Слайд 76
Один из таких шумов – гауссовский. Он возникает из за плохого освещения или при сильном нагреве камеры.

Слайд 77
Следующий шум – шум соли и перца. Он возникает как артефакт при передаче данных, когда часть пикселей на изображении теряется. Значения таких пикселей либо сильно большие и они становятся белыми, либо очень маленькие и они становятся черными. Такие шумы называются высокочастотными – это когда шум сильно отличается от самого изображения.

Слайд 78
Еще один высокочастотный шум – дробовой. Он возникает при низком освещении.
Что можно со всем этим делать?

Слайд 79
Можно применить фильтр Гаусса, по сути просто взяв и размазав наше изображение. В итоге мы получим что-то подобное:

Слайд 80
Шум уйдет, но наше изображение станет немного размытым. Если мы готовы с этим мириться, то фильтр Гаусса отличный вариант, т.к. он очень быстро работает.

Слайд 81
Но, например, для высокочастотных шумов фильтр Гаусса уже не так хорош, т.к. чтобы добиться хотя бы какого-нибудь эффекта, нужно взять очень большое ядро (ставить большую сигму) и размытие станет очень сильным. Что же нам делать в случаях с высокочастотными шумами?
Слайд 82
Можно использовать медианный фильтр. Такой фильтр уже не будет являться сверткой, хотя идея похожая. Мы будем идти скользящим окном по нашему изображению, но в новое изображение мы будем записывать медиану среди всех значений, которые попали в окно. Медиана хороша тем, что она игнорирует шумы. В результате применения такого фильтра мы получим такой результат:

Слайд 83
Такое свойство, когда фильтр не размывает изображение, называется сохранением границ. К минусам медианного фильтра можно отнести медлительность его работы по сравнению с Гауссовским.
