7 Лекция - Асимметричные криптосистемы

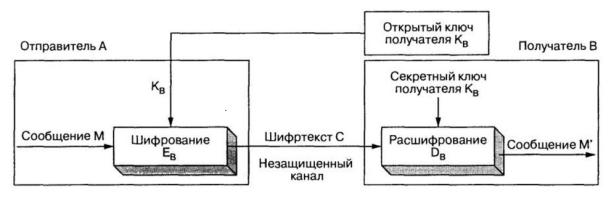
Асимметричные криптосистемы Общие положения

Еще одним обширным классом криптографических систем являются так называемые асимметричные или двухключевые системы. Эти системы характеризуются тем, что для шифрования и для расшифрования используются разные ключи, связанные между собой некоторой зависимостью. При этом данная зависимость такова, что установить один ключ, зная другой, с вычислительной точки зрения очень трудно. Один из ключей (например, ключ шифрования) может быть сделан общедоступным, и в этом случае проблема получения общего секретного ключа для связи отпадает. Если сделать общедоступным ключ расшифрования, то на базе полученной системы можно построить систему аутентификации передаваемых сообщений. Поскольку в большинстве случаев один ключ из пары делается общедоступным, такие системы получили также название криптосистем с открытым ключом.

Криптосистема с открытым ключом определяется тремя алгоритмами: генерации ключей, шифрования и расшифрования. Алгоритм генерации ключей открыт, всякий может подать ему на вход случайную строку r надлежащей длины и получить пару ключей (k1, k2). Один из ключей (например, k1) публикуется, он называется открытым, а второй, называемый секретным, хранится в тайне. Алгоритмы шифрования EB EK1 и

расшифрования DB DK2 таковы, что для любого открытого текста (сообщения) M m

DK2 EK1 m m

Рассмотрим теперь гипотетическую атаку злоумышленника на эту систему. Противнику известен открытый ключ k1, но неизвестен соответствующий секретный ключ k2. Противник перехватил криптограмму d и пытается найти сообщение m, где d EK1 m .

Поскольку алгоритм шифрования открыт, противник может просто последовательно перебрать все возможные сообщения длины n, вычислить для каждого такого сообщения mi криптограмму di EK1 mi и сравнить di с d. То сообщение, для которого di = d и будет искомым открытым текстом. Если повезет, то открытый текст будет найден достаточно быстро. В худшем же случае перебор будет выполнен за время порядка 2nT n , где T n -

время, требуемое для шифрования сообщения длины n. Если сообщения имеют длину

2

порядка 1000 битов, то такой перебор неосуществим на практике ни на каких самых мощных компьютерах.

Мы рассмотрели лишь один из возможных способов атаки на криптосистему и простейший алгоритм поиска открытого текста, называемый обычно алгоритмом полного или тотального перебора Используется также и другое название: «метод грубой силы». Другой простейший алгоритм поиска открытого текста - угадывание. Этот очевидный алгоритм требует небольших вычислений, но срабатывает с пренебрежимо малой вероятностью (при больших длинах текстов). На самом деле противник может пытаться атаковать криптосистему различными способами и использовать различные, более изощренные алгоритмы поиска открытого текста.

Кроме того, злоумышленник может попытаться восстановить секретный ключ, используя знания (в общем случае несекретные) о математической зависимости между открытым и секретным ключами. Естественно считать криптосистему стойкой, если любой такой алгоритм требует практически неосуществимого объема вычислений или срабатывает с пренебрежимо малой вероятностью. (При этом противник может использовать не только детерминированные, но и вероятностные алгоритмы.) Это и есть теоретико-сложностный подход к определению стойкости. Для его реализации в отношении того или иного типа криптографических систем необходимо выполнить следующее:

1.дать формальное определение системы данного типа;

2.дать формальное определение стойкости системы;

3.доказать стойкость конкретной конструкции системы данного типа.

Здесь сразу же возникает ряд проблем.

Во-первых, для применения теоретико-сложностного подхода необходимо, построить математическую модель криптографической системы, зависящую от некоторого параметра, называемого параметром безопасности, который может принимать сколь угодно большие значения (обычно для простоты предполагается, что параметр безопасности может пробегать весь натуральный ряд).

Во-вторых, определение стойкости криптографической системы зависит от той задачи, которая стоит перед противником, и от того, какая информация о схеме ему доступна. Поэтому стойкость систем приходится определять и исследовать отдельно для каждого предположения о противнике.

В-третьих, необходимо уточнить, какой объем вычислений можно считать «практически неосуществимым». Из сказанного выше следует, что эта величина не может быть просто константой, она должна быть представлена функцией от растущего параметра безопасности. В соответствии с тезисом Эдмондса алгоритм считается эффективным, если время его выполнения ограничено некоторым полиномом от длины входного слова (в нашем случае - от параметра безопасности). В противном случае говорят, что вычисления по данному алгоритму практически неосуществимы. Заметим также, что сами криптографические системы должны быть эффективными, т. е. все вычисления, предписанные той или иной схемой, должны выполняться за полиномиальное время.

3

В-четвертых, необходимо определить, какую вероятность можно считать пренебрежимо малой. В криптографии принято считать таковой любую вероятность, которая для любого полинома р(x) и для всех достаточно больших n не превосходит 1/p(n), где n - параметр безопасности.

Итак, при наличии всех указанных выше определений, проблема обоснования стойкости криптографической системы свелась к доказательству отсутствия полиномиального алгоритма, который решает задачу, стоящую перед противником. Но здесь возникает еще одно и весьма серьезное препятствие: современное состояние теории сложности вычислений не позволяет доказывать это отсутствие для конкретных задач рассматриваемого класса. Из этого следует, что на данный момент стойкость криптографических систем может быть установлена лишь с привлечением каких-либо недоказанных предположений. Поэтому основное направление исследований состоит в поиске наиболее слабых достаточных условий (в идеале - необходимых и достаточных) для существования стойких систем каждого из типов.

Односторонние функции и функции-ловушки

Центральным понятием в теории асимметричных криптографических систем является понятие односторонней функции.

Неформально под односторонней функцией понимается эффективно вычислимая функция, для обращения которой (т.е. для поиска хотя бы одного значения аргумента по заданному значению функции) не существует эффективных алгоритмов. Заметим, что обратная функция может и не существовать.

Формально понятие односторонней функции для двоичного случая описывается следующим образом:

Функция f называется односторонней (one-way function или функция однонаправленная), если это отображение

f :V* V*

такое, что для всех натуральных n и для множества всех x Vn существуют такие C, ,

что образ y f x любого слова x Vn длины n можно вычислить меньше чем за C n

операций (это и означает с полиномиальной сложностью), но ни для каких не

существует алгоритма, вычисляющего для всех натуральных m и для любого слова y Vm

длины m прообраз f 1 y меньше, чем за C' n операций (не существует алгоритма с

полиномиальной сложностью).

Вопрос о существовании односторонней функции является открытым. Доказательство односторонности какой-либо функции означало бы доказательство известнейшей гипотезы NP P теории сложности алгоритмов. Иногда односторонней функцией называют эффективно вычислимую функцию, для которой не известен эффективный алгоритм обращения

Функция-ловушка (trapdoor function или функция с секретом) - это функция, зависящая от параметра (секрета, описания секрета, ловушки), знание которого позволяет эффективно (т.е. с полиномиальной сложностью) вычислять и обращать данную функцию. Если параметр неизвестен, то не существует эффективного алгоритма обращения

4

функции, т.е. функция с секретом при неизвестном секрете обладает свойствами односторонней функции.

В качестве задач, приводящих к односторонним функциям, можно привести следующие.

1.Разложение числа на простые сомножители. Вычислить произведение двух простых чисел очень просто. Однако, для решения обратной задачи - разложения заданного числа на простые сомножители, эффективного алгоритма в настоящее время не существует.

2.Дискретное логарифмирование в конечном простом поле (проблема

Диффи-Хеллмана). Допустим, задано большое простое число р и пусть g - примитивный элемент поля GF(p). Тогда для любого а вычислить ga(mod р) просто, а вычислить а по заданным к = ga(mod р) и р оказывается

затруднительным.

Криптосистемы с открытым ключом основываются на односторонних функцияхловушках. При этом открытый ключ определяет конкретную реализацию функции, а секретный ключ дает информацию о ловушке. Любой, знающий ловушку, может легко вычислять функцию в обоих направлениях, но тот, у кого такая информация отсутствует, может производить вычисления только в одном направлении. Прямое направление используется для шифрования и для верификации цифровых подписей, а обратное - для расшифрования и выработки цифровой подписи.

Во всех криптосистемах с открытым ключом чем больше длина ключа, тем выше различие между усилиями, необходимыми для вычисления функции в прямом и обратном направлениях (для того, кто не обладает информацией о ловушке).

Все практические криптосистемы с открытым ключом основываются на функциях, считающихся односторонними, но это свойство не было доказано в отношении ни одной из них. Это означает, что теоретически возможно создание алгоритма, позволяющего легко вычислять обратную функцию без знания информации о ловушке. В этом случае, криптосистема, основанная на этой функции, станет бесполезной. С другой стороны, теоретические исследования могут привести к доказательству существования конкретной нижней границы сложности обращения некоторой функции, и это доказательство будет существенным событием, которое окажет значительное позитивное влияние на развитие криптографии.

Отметим, что современные асимметричные системы основаны на задачах, которые могут быть эффективно решены на квантовых вычислителях в случае их появления. Если появится квантовый вычислитель, способный решать практически значимые задачи, будут использоваться иные задачи, поиском которых занимается современная постквантовая криптография.

Асимметричные системы шифрования Криптосистема Ривеста-Шамира-Адлемана

Система Ривеста-Шамира-Адлемана (Rivest, Shamir, Adleman - RSA), первое описание которой появилось в августе 1977 года в колонке «Математические игры» в

5

журнале Scientific American, представляет собой криптосистему, стойкость которой основана на сложности решения задачи разложения числа на простые сомножители. Кратко алгоритм можно описать следующим образом:

Пользователь B выбирает пару различных простых чисел pB и qB , вычисляет число nB = pB * qB И выбирает число dB, такое что НОД(dB, nB ) = 1, где n - функция Эйлера (количество чисел, меньших n и взаимно простых с n). Если n= pq, где р и q - простые числа, то n p 1 q 1 .

Затем он вычисляет величину еB, такую, что dB *еB = 1 (mod nB ), и размещает в

общедоступной справочной таблице пару (еB, nB), являющуюся открытым ключом пользователя B. Секретным ключом является, к примеру, тройка (dB, pB, qB).

Теперь пользователь A, желая передать сообщение пользователю B, представляет исходный открытый текст x по основанию nB=n:

x = c0+c1nB+c2.(nB)2+..., ci из Zn

Пользователь A зашифровывает текст при передаче его пользователю B, применяя к коэффициентам ci, отображение EeB ,nB :

EeB ,nB ci cieB modnB yi ,

получая зашифрованное сообщение yi. В силу выбора чисел dB и еB, отображение EeB ,nB

является взаимно однозначным, и обратным к нему будет отображение

DdB ,pB ,qb yi yidB modnB .

Пользователь B производит расшифрование полученного сообщения y, применяя

DdB ,pB ,qb EdB ,pBqb .

Для того чтобы найти отображение DdB ,pB ,qb , обратное по отношению к EeB ,nB ,

требуется знание множителей nB = pB * qB

Время выполнения наилучших из известных алгоритмов разложения при n > 10145 на сегодняшний день выходит за пределы современных технологических возможностей.

Существует вариант криптосистемы RSA, в которой вместо функции Эйлера используется функция Кармайкла n , где n - наименьшее целое t, такое что для любого целого х, взаимно простого с n, выполняется хt = 1 (mod n). Если n выбирается так, как описано выше, то n = НОК(p -1,q-1)

Криптосистема Эль-Гамаля

Система Эль-Гамаля - это криптосистема с открытым ключом, основанная на проблеме дискретного логарифма. Система включает как алгоритм шифрования, так и алгоритм цифровой подписи.

Множество параметров системы включает нечетное простое число р и целое число g, степени которого по модулю р порождают большое число элементов Zp. При этом ordpg q , q| p 1. У пользователя B есть секретный ключ b (0 b q) и открытый ключ

у, где у = gb (mod р). Предположим, что пользователь A желает послать сообщение m

6

пользователю B. Сначала A выбирает случайное число k, меньше чем р. Затем он вычисляет

где обозначает побитовое "исключающее ИЛИ". Затем абонент A посылает B пару двоичных векторов (у1,у2).

После получения шифрованного текста пользователь B вычисляет

Однако, схема Эль-Гамаля не лишена определенных недостатков. Среди них можно указать следующие:

1.Отсутствие семантической стойкости. Если g - примитивный элемент Zp, то за полиномиальное время можно определить, является ли некоторое число х квадратичным вычетом, или нет. Это делается возведением в степень x(p-1)/2 mod р. Если результат равен 1, то х - квадратичный вычет по модулю р, если -

1, то х — квадратичный невычет. Далее пассивный противник проверяет, являются ли gk и gv квадратичными вычетами. gkv будет квадратичным вычетом тогда и только тогда, когда и gk, и gv будут квадратичными вычетами. Если это так, то у2 = m*ук mod р будет квадратичным вычетом,

тогда и только тогда, когда само сообщение m будет квадратичным вычетом. То есть пассивный противник получает некоторую информацию об исходном тексте, имея лишь шифрованный текст и открытый ключ получателя.

2.Делимость шифра. Если дан шифрованный текст (у1,у2), то мы можем получить другой шифрованный текст, изменив только вторую часть

сообщения. В самом деле, умножив у2 на gu (u не равно 0), мы получим шифртекст для другого сообщения m'= m*gu.

Для защиты от подобных атак Шнорром и Якобссоном было предложено объединить схему шифрования Эль-Гамаля с цифровой подписью Шнорра, что позволяет не только шифровать сообщение, но и аутентифицировать его.

Зашифрование осуществляется следующим образом. Автор сообщения выбирает случайные k,s Zq . далее он вычисляет

gk (mod р),

myk (mod р),

с = H(gs, gk, myk), z = s + сk (mod q).

Шифрованный текст представляет собой четверку (gk, myk, с, z).

Получив сообщение h, f ,c,z , приемная сторона вначале верифицирует его,

7

проверяя выполнение равенства

H gz h c , f ,h, f c.

В случае успешной верификации открытый текст получается по формуле

Заметим, что вторая половина шифрованного текста c,z зависит от исходного

сообщения только через хеш-функцию H, которая статистически независима от m, и, следовательно, не содержит никакой информации об m.

Указанными авторами было предложено обобщение данной схемы на случай, когда пространство сообщений М представляет собой произвольную аддитивную группу, например M Zqn . Используются две статистически независимые хеш-функции

H :G2 M Zq и HM :G M . В базовой схеме шифрования mук (mod р) заменяется на m + Нм(ук) из М. Верификация шифрованного текста h, f ,c,z остается без изменений, а

расшифрование будет проводиться по формуле f HM h .

Криптосистемы Меркля-Хеллмана и Хора-Ривеста

Криптосистемы Меркля-Хеллмана и Хора-Ривеста основаны на использовании односторонней функции, известной под названием "задача укладки рюкзака".

Пусть имеется n числовых объектов, так что можно составить n- компонентный вектор f или вектор f длины n, так что i-й компонент f представляет собой место, занимаемое i-м объектом (числом). Имеется рюкзак общим объемом К.

Теперь задачу укладки рюкзака может быть сформулирована следующим образом: нам даны f и К, и требуется найти битовый вектор х, такой что (f,x)=K. Известно, что не существует эффективного алгоритма вычисления х по f и К в общем случае. Таким образом, мы можем использовать вектор f для шифрования n-битного сообщения х путем вычисления произведения K=(f,x).

Важно отметить, что выбор f является критическим. Например, предположим, что f выбирается в виде супервозрастающей последовательности. В этой ситуации для любого i

fi>f1+...+fi-1

В этом случае при данных f и К вычислить х очень просто. Мы проверим, является ли К большим, чем последний элемент f, и если да, то мы делаем последний элемент х равным 1, вычитаем это значение из К и рекурсивно решаем меньшую по объему задачу. Этот метод работает, поскольку когда К больше последнего элемента f, даже если мы выберем х=(1 1 1 ... 1 0), то произведение (f,x) все равно будет слишком маленьким, благодаря тому, что последовательность супервозрастающая. Таким образом, мы должны выбирать 1 в последней позиции х.

Ясно, что выбор f очень важен - в зависимости от f мы можем получить, а можем и

8

не получить одностороннюю функцию. Однако, именно существование этого простого случая позволяет нам создать функцию-ловушку, которую мы можем использовать для построения криптосистемы с открытым ключом.

Пользователь В получает свой открытый ключ следующим образом:

1.Выбирает супервозрастающую последовательность f' примерно из n=100 элементов;

2.Выбирает случайное целое m, большее суммы элементов f';

3.Выбирает другое случайное целое w, взаимно простое с m: НОД (m,w)=1.

4.Теперь вычисляется f'' умножением каждого компонента f на w по модулю

m:f' = f w (mod m)

5.Проводится случайная перестановка Р элементов f'' для получения открытого ключа f.

Теперь В раскрывает ключ f (открытый ключ) и держит в секрете f', m, w и Р. Когда пользователь А хочет послать В сообщение (двоичный вектор) х, он

вычисляет S = (f,x) и посылает это вычисленное S. Если данная система является стойкой, тогда для внешнего наблюдателя С вычисление х по S и открытому ключу f будет эквивалентно решению задачи рюкзака в общем случае. Допустим, что предположение о стойкости верно. В этом случае, хотя С не может расшифровать сообщение, B может это сделать, применяя секретный ключ, которые он использовал при вычислении f.

Пользователь B может вычислить S'=f'х’, x’=P-1(x), так что он сможет решить задачу рюкзака в случае супервозрастающей последовательности. Вычисление S' производится следующим образом.

S'=(f',x’)=(f1'x1’+...+fn'xn’)(mod m)=w-1(wf1'x1’+...+wfn'xn’)(mod m)= = w-1(f1x1+...+fnxn)(mod m)= w-1(f,x)(mod m)= w-1S(mod m)

Таким образом, B просто умножает S на число, обратное w по умножению, по модулю m, а затем решает задачу рюкзака в случае супервозрастающей последовательности f', и теперь он сможет прочитать сообщение, применив к x’ подстановку P.

При получении ключа мы начинаем с супервозрастающей последовательности и затем скрываем имеющуюся в ней структуру. Другими словами, построенная последовательность выглядит так, что в ней нет никакой структуры. Но система может быть сделана еще более стойкой (или, по крайней мере, так будет казаться) путем повторения этого процесса скрытия структуры. Если мы выберем другие m и W, тогда мы сможем построить новый открытый ключ, который не может быть построен с использованием единственной пары (m, w). Мы можем повторять это снова и снова, и система выглядит все более и более стойкой с каждой итерацией.

В 1982 г Эди Шамир открыл атаку на криптосистему, использующую одну итерацию. Это оказалось началом падения систем, основанных на задаче рюкзака.

Допустим, что перестановка не применяется, так что f'' = f. Тогда для любого i fi =fi'w mod m

По определению модульной конгруэнтности должен существовать вектор k, такой

9

что для любого i u fi - mki = fi'

где u — это обратное к w по умножению по модулю m (напомним, что мы выбирали m и w взаимно простыми, так что это обратное существует). После этого в результате

Поскольку m очень велико, выражение справа будет очень маленьким, поэтому покомпонентное частное к и f близко к u/m. Подставляя 1 вместо i и вычитая из первоначального уравнения, получим:

fi f1 mfi mf1

Поскольку обе величины справа положительны и вычитаемое очень мало, мы можем записать:

Также заметим, что поскольку f' супервозрастающая, каждый элемент должен быть

меньше половины следующего, поэтому для любого i имеем: fi'<m*2i-n

Далее мы можем записать:

ki k1 2i n

fi f1 fi

После несложных преобразований получаем: ki f1 k1 fi f12i n

Оказывается, что поскольку f открыт, всего лишь несколько этих неравенств (три или четыре) однозначно определяют k. Эти неравенства относятся к области целочисленного программирования, поэтому k можно быстро найти, например, с помощью алгоритма Ленстры. А если мы знаем k, то мы можем легко раскрыть систему.

Допустим, что мы выполним перестановку f до опубликования, т.е. Р не является тождественной подстановкой. Поскольку нам нужны только первые 3 или 4 элемента k, мы можем просто перебрать все варианты, количество которых определяется третьей или четвертой степенью размерности k.

Вдальнейшем были разработаны методы вскрытия систем, использующих несколько итераций, и в настоящее время любая система, использующая модульное умножение для скрытия легко разрешимой задачи рюкзака, может быть эффективно раскрыта. Однако, рассмотренный метод не является единственным способом применения задачи рюкзака в криптографии.

В1986 г. Бен-Цион Хор предложил криптосистему, на сегодняшний день единственную, не использующую модульное умножение для скрытия простой задачи укладки рюкзака. Это также единственная система, основанная на задаче укладки