4. Детальные выводы по проделанной работе
4.1. Анализ устойчивости
Фильтр №1:
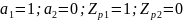
Полюс
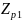находится на единичной окружности.
Фильтр находится на границе устойчивости.
Фильтр №2:
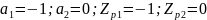
Полюс находится на единичной окружности. Фильтр находится на границе устойчивости.
Фильтр №3:
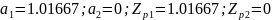
Полюс находится за пределами единичной окружности. Фильтр не является устойчивым.
Фильтр №4:
Полюс находится за пределами единичной окружности. Фильтр не является устойчивым.
Фильтр №5:
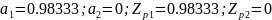
Полюс находится внутри единичной окружности. Фильтр является устойчивым.
Фильтр №6:
Полюс находится внутри единичной окружности. Фильтр является устойчивым.
Фильтр №7:
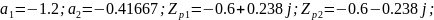
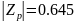
Полюсы являются комплексно-сопряженными и находятся внутри единичной окружности. Фильтр является устойчивым.
Фильтр №8:
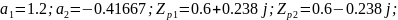
Полюсы являются комплексно-сопряженными и находятся внутри единичной окружности. Фильтр является устойчивым.
Фильтр №9:
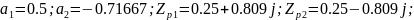
Полюсы являются комплексно-сопряженными и находятся внутри единичной окружности. Фильтр является устойчивым.
Фильтр №10:
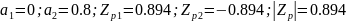
Полюсы являются комплексно-сопряженными и находятся внутри единичной окружности. Фильтр является устойчивым.
4.2. Классификация исследуемых цф
По определению АЧХ любого ЦФ определяется
по формуле (17). Так как
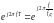- периодическая функция частоты
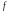с периодом
,
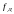то и
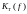будет периодической функцией, т.е. :
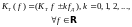(36)
Частота
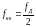называется частотой Найквиста и для
любого ЦФ с вещественными параметрами,
его АЧХ симметрично относительно частоты
Найквиста
,
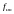следовательно:
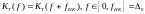(37)
в рабочем диапазоне частот
.
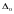Исходя из этого свойства, можно сделать
вывод, что вся полезная информация о
поведении фильтра в частотной области
заключена только в диапазоне
.
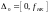В интервале
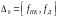поведение АЧХ лишь зеркально отображается
и не несет новой информации.
Центральной частотой ЦФ называется величина:
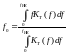(38)
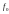– является «центром тяжести» кривой
АЧХ ЦФ
в рабочем диапазоне
.
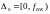ЦФ с АЧХ
называется НЧ (ФНЧ), если
примыкает к частоте
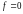и находится в промежутке рабочего
диапазона
.
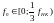ЦФ с АЧХ
называется ВЧ (ФВЧ), если
примыкает к частоте
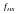и находится в промежутке рабочего
диапазона
.
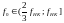ЦФ с АЧХ
называется П (ПФ), если
находится в середине рабочего диапазона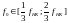
.
ЦФ с АЧХ
называется Р (РФ), если его дополнительная
АЧХ
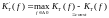описывает
полосовой фильтр.
При
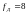кГц
значения границ промежутков рабочих
диапазонов будут равны:
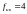кГц,
кГц,
кГц.
Классификация фильтров по значению центральной частоты ЦФ:
- Фильтр №5 (
= 1;
= 0.98333;
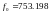Гц) является ФНЧ 1-го порядка.
- Фильтр №6 (
= 1;
= -0.98333;
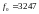Гц) является ФВЧ 1-го порядка.
- Фильтр №7 (
=
1;
=
-1.2;
=-0.41667;
Гц) является ФВЧ 2-го порядка.
- Фильтр №8 (
=
1;
=
1.2;
=
-0.41667;
Гц) является ФНЧ 2-го порядка.
- Фильтр №9 (
=
1;
=
0.5;
=-0.71667;
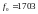Гц) является ПФ 2-го порядка.
- Фильтр №10 (
=
1;
=
0;
= 0.8;
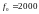Гц) является РФ 2-го порядка.