- •2.3. Построение структурной схемы цф
- •2.4. Расчет и построение характеристик цф
- •3. Выполнение лабораторной работы
- •3.1. Исходные параметры исследуемых фильтров
- •3.2. Структурные схемы и уравнения исследуемых фильтров
- •3.3. Выражения для расчета характеристик исследуемых цф
- •3.4. Результаты экспериментального исследования
- •4. Детальные выводы по проделанной работе
- •4.1. Анализ устойчивости
- •4.2. Классификация исследуемых цф
- •4.3. Анализ поведения ачх
- •4.4. Преимущества и недостатки рекурсивных цф
МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
Московский технический университет
связи и информатики
────────────────────────────────────
Факультет СиСС
Кафедра общей теории связи
ЛАБОРАТОРНАЯ РАБОТА
№26-2
по дисциплине «Цифровая обработка сигналов»
на тему:
«Анализ рекурсивных цифровых фильтров
1-го и 2-го порядка»
Вариант №12
Выполнил: студ. гр. БЗС2002
Ломакин Алексей
Проверил: проф. каф. ОТС
Волчков В. П.
(Осенний семестр)
Москва 2022
1. Цель работы
На персональном компьютере провести анализ рекурсивных цифровых фильтров (ЦФ) 1-го и 2-го порядка; исследовать частотные и временные характеристики фильтров, их взаимосвязь со значениями коэффициентов ЦФ; определить области устойчивости рекурсивных фильтров 1 и 2 порядка
2. Выполнение домашнего задания
2.1. Исходные данные для своего варианта ДЗ
В соответствии с вариантом, исходные данные в таблице 1.
Табл. 1. Таблица параметров фильтра для 12 варианта ДЗ
Порядок фильтра |
|
|
|
1 |
1,0 |
-0,87 |
8 кГц |
2.2. Запись разностного уравнения и системной функции
Цифровой фильтр – это цифровая или дискретная система и для её описания используется разностное уравнение с постоянными коэффициентами. По условию коэффициенты выходного сигнала равны 0, поэтому разностное уравнение ЦФ 1-го порядка будет выглядеть следующим образом:
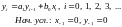 (1)
(1)
В данной формуле:
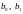 - коэффициенты разностного уравнения;
- коэффициенты разностного уравнения;
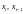 - входной сигнал с задержкой 0, 1, ...;
- входной сигнал с задержкой 0, 1, ...;
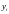 - выходной сигнал
- выходной сигнал
Подставив в формулу (1) исходные данные из табл. 1, получим:
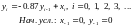 (2)
(2)
Пусть задан дискретный сигнал
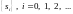 .
Тогда его односторонним Z-преобразованием
называется:
.
Тогда его односторонним Z-преобразованием
называется:
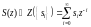 (3)
(3)
Пусть на входе ЦФ действует сигнал
 ,
а на выходе наблюдается сигнал
,
а на выходе наблюдается сигнал
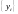 .
Тогда системной функцией ЦФ называется
отношение:
.
Тогда системной функцией ЦФ называется
отношение:
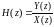 (4)
(4)
Для
 -
преобразования нужно определить
некоторые его свойства, такие как
свойство линейности и смещение. Свойство
линейности
-
преобразования:
-
преобразования нужно определить
некоторые его свойства, такие как
свойство линейности и смещение. Свойство
линейности
-
преобразования:
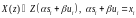 (5)
(5)
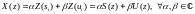 (6)
(6)
Свойство смещения Z-преобразования:
 (7)
(7)
Системная функция рекурсивного ЦФ находится с помощью:
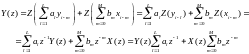 (8)
(8)
Приравняем левую и правую части:
 (9)
(9)
Таким образом, используя свойство пропорции системная функция рекурсивного фильтра рассчитывается как:
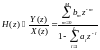 (10)
(10)
После подстановки исходных данных в уравнение (10), получим системную функцию рекурсивного ЦФ 1-го порядка в соответствии с вариантом:
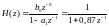 (11)
(11)
2.3. Построение структурной схемы цф
Структурная схема фильтра, составленная на основе уравнения (2), показана на рис. 1

Рис. 1. Структурная схема рекурсивного
ЦФ 1-го порядка (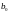 =
1;
=
1;
 =
-0,87)
=
-0,87)
2.4. Расчет и построение характеристик цф
Импульсная реакция – отклик ЦФ на входной единичный импульс:
 (12)
(12)
где
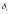 -
единичный импульс Кронекера:
-
единичный импульс Кронекера:
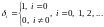 (13)
(13)
В соответствии с формулами (1) и (12) и начальными условиями получаем импульсную реакцию заданного рекурсивного ЦФ 1-го порядка:
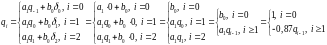 (14)
(14)
Г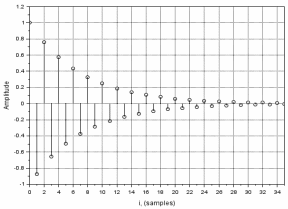 рафик
импульсной реакции
рафик
импульсной реакции
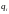 ,
построенный с использованием средств
математического пакета Scilab
изображен на рис. 2.
,
построенный с использованием средств
математического пакета Scilab
изображен на рис. 2.
Рис. 2. Импульсная реакция рекурсивного ЦФ 1-го порядка ( = 1; = -0,87)
Переходная функция – это отклик ЦФ на дискретный единичный скачок:
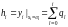 (15)
(15)
В соответствии с формулами (1) и (15) и начальными условиями получаем переходную характеристику заданного рекурсивного ЦФ 1-го порядка:
 (16)
(16)
График переходной характеристики по
переходной функции
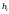 ,
построенный с использованием средств
математического пакета MatLab,
изображен на рис. 3.
,
построенный с использованием средств
математического пакета MatLab,
изображен на рис. 3.
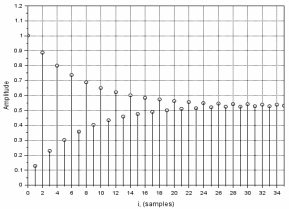
Рис. 3. Переходная характеристика (ПХ) ЦФ 1-го порядка ( = 1; = -0,87)
Комплексным коэффициентом передачи ЦФ
 называется функция частоты
называется функция частоты :
:
 (17)
(17)
где
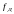 -частота
дискретизации,
-частота
дискретизации,
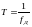 -интервал
дискретизации.
-интервал
дискретизации.
Амплитудно-частотной характеристикой ЦФ называется функция частоты:
 (18)
(18)
Где
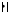 -оператор
взятия модуля комплексного числа. По
определению модуля комплексного числа
-оператор
взятия модуля комплексного числа. По
определению модуля комплексного числа
 :
:
 (19)
(19)
Также по формуле Эйлера:
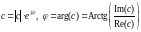 (20)
(20)
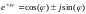 (21)
(21)
Следовательно, АЧХ ЦФ рассчитывается по следующей формуле:
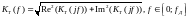 (22)
(22)
Где реальная
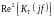 и мнимая
и мнимая
 части:
части:
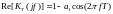 (23)
(23)
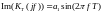 (24)
(24)
Если в уравнении (11) произвести замену
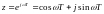 ,
где
,
где
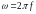 - круговая частота, [рад/с],
- круговая частота, [рад/с],
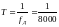 -
период дискретизации, [с] и взять модуль,
получится АЧХ ЦФ:
-
период дискретизации, [с] и взять модуль,
получится АЧХ ЦФ:
 (25)
(25)
График амплитудно-частотной характеристики
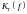 ,
построенный с использованием средств
математического пакета Scilab,
изображен на рис. 4.
,
построенный с использованием средств
математического пакета Scilab,
изображен на рис. 4.
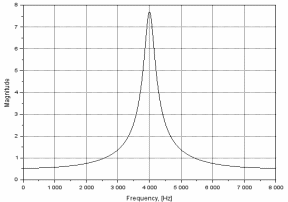
Рис. 4. АЧХ рекурсивного ЦФ 1-го порядка ( = 1; = -0,87)
Рассчитаем
ФЧХ ЦФ, найдя аргумент
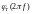 функции
функции
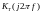 :
:
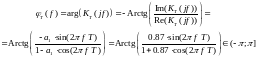 (26)
(26)
График фазо-частотной характеристики
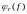 ,
построенный с использованием средств
математического пакета Scilab,
изображен на рис. 5.
,
построенный с использованием средств
математического пакета Scilab,
изображен на рис. 5.
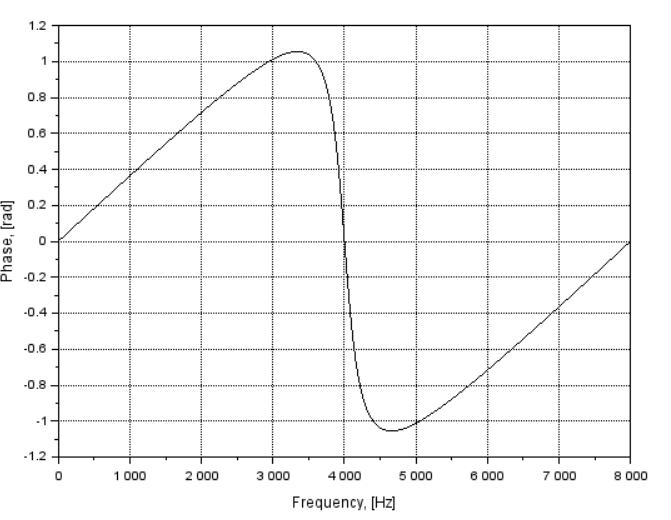
Рис. 5. ФЧХ рекурсивного ЦФ 1-го порядка ( = 1; = -0,87)
3. Выполнение лабораторной работы
3.1. Исходные параметры исследуемых фильтров
В соответствии с вариантом, исходные данные в таблице 2.
Табл. 2. Таблица параметров исследуемых фильтров
Номер фильтра |
Порядок фильтра |
|
|
|
1 |
1 |
1 |
1 |
0 |
2 |
1 |
1 |
-1 |
0 |
3 |
1 |
1 |
1.01667 |
0 |
4 |
1 |
1 |
-1.01667 |
0 |
5 |
1 |
1 |
0.98333 |
0 |
6 |
1 |
1 |
-0.98333 |
0 |
7 |
2 |
1 |
-1.2 |
-0.41667 |
8 |
2 |
1 |
1.2 |
-0.41667 |
9 |
2 |
1 |
0.5 |
-0.71667 |
10 |
2 |
1 |
0 |
0.8 |