Глава 2. Методы моделирования сушки пористых тел

2.1. Конечно-элементный метод моделирования

Моделирование методом конечных элементов (FEM), также известное как анализ конечных элементов (FEA), представляет собой численный метод, используемый для прогнозирования характеристик структурных, тепловых, жидкостных, электромагнитных и других физических систем. Метод требует, чтобы изучаемый компонент был разбит на дискретные элементы, в результате чего получилась сетка конечных элементов. Простые уравнения, описывающие поведение отдельных элементов, затем собираются в более крупную систему уравнений, моделирующую всю проблему. В зависимости от наличия нелинейных эффектов результирующая система уравнений решается прямым или итерационным решателем.[8]

Истоки метода конечных элементов можно отнести к началу 1940-х годов в США, с дальнейшим развитием в 50-х и начале 60-х годов в Китае и СССР. Универсальные программы стали доступны только в 1968 году, с появлением спонсируемого НАСА NASTRAN. Сегодня доступно множество комплексных пакетов FEA, включая несколько версий NASTRAN и многие другие: ANSYS, ABAQUS, HyperWorks и LS/DYNA, и это лишь некоторые из них.

Точность результатов FEA зависит от многих факторов, включая уточнение сетки конечных элементов, тип используемых элементов, знание свойств материала FEA, знание реальных условий нагрузки и способность точно моделировать физическую проблему. Группа услуг FEA компании Kinetic Vision использует несколько систем контроля качества, включая контрольные списки контроля качества и экспертную оценку.[13]

Описание законов физики для задач, зависящих от пространства и времени, обычно выражается с помощью уравнений в частных производных (УЧП). Для подавляющего большинства геометрий и задач эти УЧП не могут быть решены аналитическими методами. Вместо этого можно построить аппроксимацию уравнений, обычно на основе различных типов дискретизации . Эти методы дискретизации аппроксимируют УЧП с помощью уравнений численной модели, которые можно решить с помощью численных методов. Решение уравнений численной модели, в свою очередь, является аппроксимацией реального решения УЧП. Для расчета таких приближений используется метод конечных элементов (МКЭ ) .

Возьмем, например, функцию u, которая может быть зависимой переменной в УЧП (т. е. температура, электрический потенциал, давление и т. д.). Функция u может быть аппроксимирована функцией uh, используя линейные комбинации базисных функций в соответствии с уравнением следующие выражения:

(1)

и

(2)

Здесь ψ i обозначает базисные функции, а ui обозначает коэффициенты функций, которые приближают u с помощью u h . Рисунок ниже иллюстрирует этот принцип для одномерной задачи. u может, например, представлять температуру по длине (x) стержня, который неравномерно нагрет. Здесь линейные базисные функции имеют значение 1 в соответствующих узлах и 0 в других узлах. В этом случае на участке оси x, где определена функция u (т. е. длина стержня), имеется семь элементов.[8]

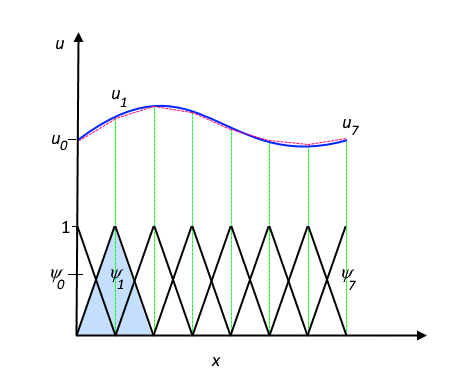
Рисунок 4– Функция u (сплошная синяя линия) аппроксимируется с помощью u h (пунктирная красная линия), которая представляет собой линейную комбинацию линейных базисных функций ( ψ i представлена сплошными черными линиями). Коэффициенты обозначены от u 0 до u 7 .

Одним из преимуществ использования метода конечных элементов является то, что он предлагает большую свободу в выборе дискретизации как элементов, которые можно использовать для дискретизации пространства, так и базисных функций. Например, на рисунке выше элементы равномерно распределены по оси x, хотя это не обязательно. Также можно было применить элементы меньшего размера в области, где градиент u велик, как показано ниже.

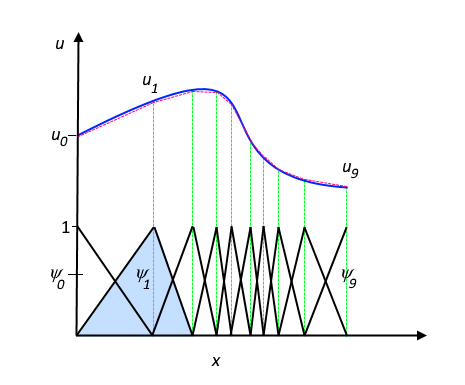
Рисунок 5 – Функция u (сплошная синяя линия) аппроксимируется с помощью u h (пунктирная красная линия), которая представляет собой линейную комбинацию линейных базисных функций ( ψ i представлена сплошными черными линиями). Коэффициенты обозначены от u 0 до u 7 .

Оба этих рисунка показывают, что выбранные линейные базисные функции имеют очень ограниченную поддержку (отличную от нуля только в узком интервале) и перекрываются вдоль оси x. В зависимости от решаемой задачи вместо линейных функций могут быть выбраны другие функции.

Еще одним преимуществом метода конечных элементов является то, что теория хорошо разработана. Причиной этого является тесная связь между численной постановкой и слабой постановкой задачи УЧП. Например, теория дает полезные оценки ошибок или границы ошибки, когда уравнения численной модели решаются на компьютере.[9]

Допустим, существует твердое тело, температура которого меняется во времени, но изменения в пространстве незначительны. В этом случае уравнение сохранения внутренней (тепловой) энергии может привести к уравнению изменения температуры с очень небольшим изменением во времени под действием источника тепла g :

(3)

Здесь обозначает плотность, а C p обозначает теплоемкость. Температура T является зависимой переменной, а время t является независимой переменной. Функция может описывать источник тепла, который меняется в зависимости от температуры и времени. уравнение (3) утверждает, что если происходит изменение температуры во времени, то это должно быть уравновешено (или вызвано) источником тепла . Уравнение представляет собой дифференциальное уравнение, выраженное через производные одной независимой переменной ( t ). Такие дифференциальные уравнения известны как обыкновенные дифференциальные уравнения (ОДУ).

В некоторых ситуациях знание температуры в момент времени t 0, называемой начальным условием, позволяет аналитически решить уравнение. (3) что выражается как:

(4)

Таким образом, температура в твердом теле выражается через алгебраическое уравнение (4), где значение времени t 1 возвращает значение температуры T 1 в этот момент.

Часто существуют различия во времени и пространстве. Например, температура в твердом теле в положениях, близких к источнику тепла, может быть немного выше, чем в других местах. Такие изменения дополнительно приводят к возникновению теплового потока между различными частями твердого тела. В таких случаях сохранение энергии может привести к уравнению теплопередачи, которое выражает изменения как во времени, так и в пространственных переменных (x), например:[9]

(5)

Как и раньше, T — зависимая переменная, а x ( x = ( x, y, z )) и t — независимые переменные. Вектор теплового потока в твердом теле обозначается q = ( q x, q y, q z ), а дивергенция q описывает изменение теплового потока по пространственным координатам. Для декартовой системы координат расхождение q определяется как:

(6)

Таким образом, (5) утверждает, что если происходит изменение чистого потока, когда изменения добавляются во всех направлениях так, что дивергенция (сумма изменений) q не равна нулю, то это должно быть уравновешено (или вызвано) теплом источник и/или изменение температуры во времени (накопление тепловой энергии).[13]

Тепловой поток в твердом теле можно описать определяющим соотношением для теплового потока за счет проводимости, также называемым законом Фурье :

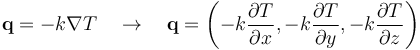(7)

В приведенном выше уравнении k обозначает теплопроводность. уравнение (7) утверждает, что тепловой поток пропорционален градиенту температуры, а теплопроводность является константой пропорциональности. уравнение (7) в (5) дает следующее дифференциальное уравнение:

(8)

Здесь производные выражаются через t, x, y и z . Когда дифференциальное уравнение выражается через производные более чем одной независимой переменной, оно называется уравнением в частных производных (УЧП), поскольку каждая производная может представлять собой изменение в одном направлении из нескольких возможных направлений. Также обратите внимание, что производные в ОДУ выражаются с помощью d, а частные производные выражаются с использованием более фигурного ∂ .

В дополнение к уравнению (8) также могут быть известны температура в момент времени t 0 и температура или тепловой поток в некоторой позиции x0. Такие знания могут быть применены в начальных и граничных условиях для уравнения. (8). Во многих ситуациях PDE не могут быть решены аналитическими методами, чтобы получить значения зависимых переменных в разное время и в разных положениях. Например, может быть очень сложно или невозможно получить такое аналитическое выражение, как:[11]

(9)

Вместо аналитического решения УЧП альтернативным вариантом является поиск приближенных численных решений для решения уравнений численной модели. Метод конечных элементов — это именно такой метод — численный метод решения уравнений в частных уравнениях.

Подобно сохранению тепловой энергии, упомянутому выше, можно вывести уравнения сохранения импульса и массы, которые составляют основу гидродинамики. Кроме того, уравнения для электромагнитных полей и потоков могут быть получены для задач, зависящих от пространства и времени, образующих системы УЧП.