1.2. Математические модели сушки материалов
Для понимания хода реакций необходимы знания термодинамики и кинетики. Скорость, с которой протекает реакция, является результатом действия движущей силы и сопротивления изменениям. Таким образом, существует тесная связь между термодинамикой и кинетикой
Следовательно, изучение кинетики сушки поможет определить подходящие методы сушки и контролировать процессы сушки. Это также важно для проектирования и оптимизации процессов. Кинетика сушки используется для выражения процесса удаления влаги и его связи с переменными процесса, и, следовательно, хорошее понимание скорости сушки важно для разработки модели сушки[7].
Несмотря на суть кинетики, моделирование сушки материалов в виде частиц или тонкого слоя необходимо для понимания фундаментального механизма переноса и является предпосылкой для успешного моделирования или масштабирования всего процесса для оптимизации или управления условиями эксплуатации. Простые модели, имеющие разумный физический смысл, эффективны для инженерных целей. Математическое моделирование процесса сушки является неизбежной частью проектирования, разработки и оптимизации сушилки. В основном это включает детальное исследование кинетики сушки, которое описывает механизмы и влияние, которое определенные переменные процесса оказывают на перенос влаги. Другими словами, его можно использовать для изучения переменных сушки, оценки кинетики сушки и оптимизации параметров и условий сушки. Правильная конструкция сушилки требует знания характеристик высушиваемого материала и кинетики сушки. Отмечается , что более высокая температура подразумевает большую движущую силу теплопередачи. Это также ускоряет процесс сушки, так как температура обеспечивает больший дефицит давления водяного пара.
Основными механизмами сушки являются поверхностная диффузия на поверхности пор, диффузия жидкости или пара из-за разницы в концентрации влаги и капиллярное действие в гранулированных и пористых пищевых продуктах из-за поверхностных сил. Обычно гигроскопичные продукты высыхают с постоянной скоростью и в последующие периоды снижения скорости, а сушка прекращается, когда устанавливается равновесие. Период сушки с постоянной скоростью, физическая форма продукта и внешние условия, такие как температура, скорость сушильного воздуха, направление воздушного потока и относительная влажность, оказывают большое влияние на поверхность высушиваемого продукта при поверхностной диффузии[12].
Когда поверхностная пленка твердых веществ или частиц кажется высушенной и содержание влаги снижается до критического значения, тогда начинается первый период скорости падения. В отличие от периодов постоянной скорости, период падающей скорости контролируется диффузией жидкости в результате разницы в концентрации влаги и внутренних условий продукта. Внутренние условия, такие как содержание влаги, температура и структура продукта, играют важную роль в периоды снижения скорости падения. Затем это явление сменяется вторыми периодами падения скорости сушки, а именно диффузией пара из-за разницы в концентрации влаги, а также внутренних условий продуктов. Принято считать, что явление высыхания биопрепаратов в период падения скорости контролируется механизмом диффузии жидкости и/или пара. Однако для сушки пищевых материалов, как правило, применимы только теории капиллярной и жидкостной диффузии. Диффузия является доминирующим физическим механизмом, определяющим движение влаги в материале, которое зависит от содержания влаги в образцах. Содержание влаги выражалось в пересчете на сухое вещество, что более удобно для моделирования[18].
На рисунке 3 показана зависимость скорости и температуры сушки от времени. Эту кривую скорости также можно использовать для определения доминирующего механизма продукта во время сушки. В начальный период сушки равновесная температура воздуха обычно превышает температуру продукта. Следовательно, скорость сушки между А и В увеличивается с увеличением температуры продукта до тех пор, пока температура поверхности не достигнет равновесия (соответствует линиям от В до С). В постоянных условиях процесс сушки сельскохозяйственных и биологических продуктов описывается как ряд стадий, состоящих также из начального периода постоянной скорости (В-С), в течение которого сушка происходит так, как будто испаряется чистая вода, и одного или нескольких падающих периоды скорости, когда движение влаги контролируется комбинированными внешними и внутренними сопротивлениями или внешним или внутренним сопротивлением тепло- и массообмену.
Сушка обычно прекращается, когда достигается устойчивое равновесие. В период постоянной скорости физическая форма влияет на продукт, особенно на поверхность продукта. Этот период в значительной степени контролируется капиллярными и гравитационными силами. Условия процесса сушки, такие как температура, скорость воздуха для сушки и относительная влажность, также влияют на продукт на этом этапе. Первый период скорости падения (от C до D) начинается, когда поверхностная пленка продукта кажется сухой, а содержание влаги снижается до критического значения. По мере продолжения сушки материал будет испытывать переход от первого периода скорости падения к явлению, известному как второй период скорости падения (от D до E) [4]
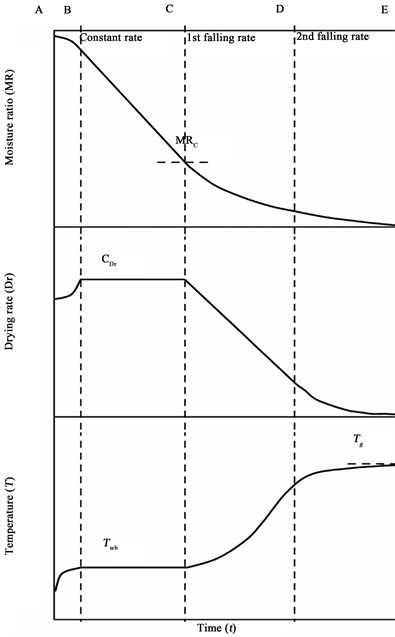
Рисунок 3 – Типичная кривая сушки сельскохозяйственной продукции, показывающая периоды постоянной скорости и падающей скорости
В литературе упоминается несколько моделей, таких как теоретическая, эмпирическая и полуэмпирическая для анализа сушки гигроскопических продуктов. Но наиболее широко применяемыми категориями моделей тонкого слоя являются полутеоретические и эмпирические модели.[14]
Математические модели сушки материалов можно классифицировать по различным критериям:
Эмпирические модели основываются на экспериментальных данных и часто используют упрощенные предположения для описания процесса. Они подходят для конкретных условий и материалов, но обладают ограниченной обобщаемостью.
Полуэмпирические модели сочетают теоретические основы с экспериментальными данными для более точного описания процесса. Такие модели часто включают параметры, которые подгоняются под определенные условия сушки.
Теоретические модели строятся на основе фундаментальных физических законов, таких как законы сохранения массы и энергии, а также уравнения тепло- и массопереноса. Они могут быть сложными в реализации, но позволяют анализировать процесс сушки более глубоко и предсказывать поведение материала при различных условиях.
Математические модели сушки находят широкое применение в промышленности для:
Проектирования сушильного оборудования: Модели помогают определить оптимальные размеры и формы оборудования, а также условия процесса (температура, влажность, скорость воздуха), чтобы максимизировать эффективность и минимизировать затраты.
Оптимизации процессов: Использование моделей позволяет проводить численные эксперименты для нахождения наилучших условий процесса, что особенно важно при масштабировании производства.
Контроля качества: Моделирование помогает предсказать и контролировать изменения в свойствах материалов, такие как текстура, влажность, форма и размер, что критически важно для сохранения качества конечной продукции.
Научные исследования в области математического моделирования сушки фокусируются на разработке более точных и универсальных моделей, которые могут быть адаптированы к различным типам материалов и условиям процесса. Особое внимание уделяется включению комплексных физико-химических процессов, таких как реакции разложения, изменения в микроструктуре и динамике фазовых переходов.
Также разрабатываются методы улучшения численных алгоритмов для повышения скорости и точности расчетов, что особенно важно для реализации моделей в реальном времени на производстве.
Математическое моделирование процессов сушки материалов является неотъемлемой частью современной промышленности, обеспечивая эффективность и инновационность производственных процессов. Развитие и улучшение математических моделей продолжает быть активной и значимой областью исследований, направленной на создание более устойчивых и экономически выгодных производственных технологий.