
20060710
.pdfВ этом случае мультипликативное и аддитивное отношения выражаются только через фазовые диаграммы
|
rm (θ ) = |
|
exp(iΦ1(θ )) |
|
= exp(iΔΦ(θ )), |
|
|
||
|
exp(iΦ2 (θ )) |
|
(62) |
||||||
|
|
|
|
|
|
||||
|
exp(iΦ1 |
(θ ))− exp(iΦ2 (θ )) |
|
ΔΦ(θ ) |
|||||
ra (θ ) = |
|
||||||||
exp(iΦ1 |
(θ ))+ exp(iΦ2 (θ )) |
= i tg |
2 |
. |
|
||||
|
|
|
|
||||||
Отношение амплитуд ρ (θ ) и разность фаз ΔΦ(θ ) принято называть мультипликативными, а ρa (θ ) и tg(ΔΦ(θ )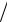 2) – аддитив-
2) – аддитив-
ными функциями угла θ [1, 2].
Между амплитудными отношениями (60) существует связь:
|
1 + ρa(θ ) |
|
ρa(θ ) − 1 |
|
ρ(θ ) = |
1 − ρa(θ ) |
, ρ(θ ) = |
ρa(θ ) + 1 . |
(63) |
Особенностью аддитивного (суммарно-разностного) представления является то, что отношение сигналов ra (θ ) и при амплитуд-
ном, и при фазовом методе пеленгации являются амплитудными функциями: при амплитудном методе ρa (θ ) на действительной
оси и при фазовом – ra (θ ) на мнимой. Следовательно, разность
фаз сигналов на входе пеленгатора при фазовом методе преобразуется в амплитуду сигнала на выходе.
Угловой дискриминатор, в котором для образования пеленгационной характеристики используется мультипликативная функция угла, реагирующий только на амплитудные соотношения принятых сигналов, называется амплитудным, а реагирующий только на фазовые соотношения – фазовым. Угловой дискриминатор, который реагирует как на амплитудные, так и на фазовые соотношения сигналов и в котором для формирования пеленгационной характеристики применяется аддитивная функция угла, называется суммарно-разностным.
Таким образом, возможны только три различных способа измерения угла (три типа угловых дискриминаторов): амплитудный, фазовый и суммарно-разностный. Каждый из них можно применять либо при амплитудном, либо при фазовом, либо при комплексном пеленговании. Поэтому возможно всего девять ос-
31

новных классов пеленгационных систем, классификация которых приведена ниже в таблице. Исходя из принятой классификации, в названии пеленгационных систем первое слово характеризует вид пеленгования, а второе – тип углового дискриминатора. Так, например, система с амплитудным угловым дискриминатором при амплитудном пеленговании называется амплитудноамплитудной, а при фазовом пеленговании – фазовоамплитудной. Система с фазовым угловым дискриминатором при амплитудном пеленговании называется амплитудно-фазовой, а при фазовом – фазово-фазовой. Система с суммарно-разностным угловым дискриминатором в зависимости от вида пеленгования называется амплитудной суммарно-разностной или комплексной суммарно-разностной.
Способ измерения |
Основные классы систем для трех видов |
||||
(тип углового дискри- |
|
пеленгования |
|
||
минатора) |
амплитудного |
|
фазового |
|
комплексного |
|
(А) |
|
(Ф) |
|
(К) |
Амплитудный (А) |
АА |
|
ФА |
|
КА |
Фазовый (Ф) |
АФ |
|
ФФ |
|
КФ |
Суммарно-разностный |
АСР |
|
ФСР |
|
КСР |
(СР) |
|
|
|
|
|
Из указанных в таблице девяти возможных систем на практике наибольшее применение находят четыре: амплитудноамплитудная (АА), фазово-фазовая (ФФ), амплитудная суммар- но-разностная (АСР) и фазовая суммарно-разностная (ФСР).
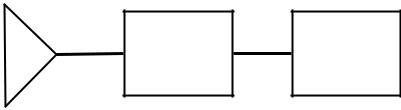
Исходя из последовательности операций, выполняемых пеленгационной системой, структурная схема ее должна содержать следующие основные элементы (рис. 16):
–угловой датчик 1, формирующий сигналы, в соотношениях параметров которых содержится информация об угловом положении источника излучения;
–преобразователь информации 2, осуществляющий изменение формы соотношения сигналов r(θ ) ;
–угловой дискриминатор 3, выделяющий вещественную функцию отношения параметров сигналов, однозначно связанную
суглом прихода электромагнитной волны от источника излучения.
32
1 |
2 |
3 |
Рис. 16. Структурная схема пеленгационной системы
Вкачестве преобразователя применяется фазовращатель на
π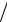 2 , выполняющий операцию умножения на ± i , и суммарно-
2 , выполняющий операцию умножения на ± i , и суммарно-
разностный преобразователь в виде кольцевого волнового моста или двойного волнового тройника [4].
Сравнение сигналов (образование отношения r(θ ) ) может
быть осуществлено в разные моменты времени в одном канале или в один и тот же момент времени, но в разных каналах. В соответствии с этим различают системы с последовательной и параллельной обработкой сигналов. В системах первого типа, одноканальных, луч антенны перемещается в пространстве по заданному закону относительно направления на источник. Наиболее распространено коническое сканирование, при котором луч перемещается по конической поверхности под углом θ0 к равно-
сигнальному направлению. При методе переключения положение луча дискретно меняется в одной или двух ортогональных плоскостях. Угловое расстояние 2θ0 между положениями луча в
каждой плоскости меньше ширины диаграммы направленности. Сканирование может осуществляться перемещением всей ан-
тенны. Однако при простоте ее радиотехнической схемы в этом случае существенно повышаются требования к жесткости конструкции антенны и к динамическим характеристикам ее привода. Обычно для сканирования механическим или электрическим способом в раскрыве создается линейное фазовое распределение, плоскость наклона фазы меняется (например, за счет поворота вокруг оси антенны смещенного с нее фазового центра облучателя). В системах последовательного типа пеленгационная характеристика на выходе углового дискриминатора находится в результате обработки сигнала в течение некоторого времени, равного, как минимум, периоду сканирования. При флуктуирующем сигнале от источника системы с параллельной обработкой сигнала более предпочтительны, поскольку сравниваемые сигналы в них
33

принимаются одновременно разными приемными устройствами. Эти системы получили название моноимпульсных [1, 3], так как в принципе одного импульса (радиолокация) достаточно для определения координат источника. Оба типа систем основаны на общих физических принципах и имеют много общего, по крайней мере, в части, касающейся антенн. Далее в качестве примера использования амплитудного метода будут рассмотрены основные пеленгационные характеристики сканирующих антенн.
Пеленгационные характеристики при коническом сканировании
Требование зеркальной симметрии диаграмм f1 и f2 (формулы (58)) выполняется в случае, когда диаграмма произвольной формы f (θ ,ϕ ) вращается вокруг оси, смещенной по координате ϑ′ на угол θ0 относительно максимума (или вокруг фазового
центра в фазовых методах) (см. рис. 17). Связанная с диаграммой система координат ϑ′,ϕ ′ поворачивается относительно отсчетной
системы координат ϑ,ϕ на угол χ . Радиус-вектор точки М, в ко-
торой находится источник, равен θ в местной системе координат, полярная ось которой совпадает с направлением максимума диаграммы, и θи в системе координат ϑ,ϕ , полярный угол равен
ψ и χи соответственно. |
Из треугольника ОМО' |
находим |
|
||||||
θ 2 = (θ |
0 |
− θ |
и |
)2 + 2θ θ |
(1 − Cos(χ − χ |
и |
)), |
(64) |
|
|
|
|
0 и |
|
|
|
|||
tgψ = Sin(χ − χи) |
(Cos(χ − χи) − θ0 |
|
θи ). |
(65) |
|||||
В простейшем случае диаграммы F(θ ) с круговой симметрией зависимость от угла ψ пропадает. Таким образом, сигнал, принятый антенной, пропорционален амплитудной диаграмме F(θ ) (θ из (73)) и меняется с изменением угла χ . Для последова-
тельных методов образования пеленгационной характеристики угол χ является функцией времени. В моноимпульсных методах
используются диаграммы с различными значениями χ .
34

Рис. 17. Геометрия смещения оси диаграммы направленности антенны
Рассмотрим ситуацию, когда пеленгация осуществляется путем конического сканирования смещенным с оси лучом. При коническом сканировании за счет вращения облучателя, фазовый центр которого не совпадает с осью вращения, принятый сигнал модулирован по амплитуде. Сигнал в антенне U (t) ~ F(θ (χ )) , где θ (χ )
определяется формулой (73), а χ = Ωt – частота сканирования лу-
ча. Амплитуда колебаний огибающей сигнала дает информацию о смещении θи источника относительно равносигнального направле-
ния, а ее фаза, т.е. положение максимума tи в долях периода сканирования, – об угловом смещении χи от оси ϑ (рис. 18). Максимум огибающей равен F(θ0 − θ ), положение его χи = χ = Ωtи , минимум F(θ0 + θ) расположен в точке χ1 = χ + π .
Рис. 18. Временная диаграмма сигнала на выходе антенны
35

Сигнал ошибки угломерной системы находится в этом случае нормировкой разложения в ряд Фурье сигнала U (t) к постоянной
составляющей разложения:
r(t) = 1 + ρ1Cos(Ωt −ψ1 )+ ρ2Cos(2Ωt −ψ 2 )+ |
(66) |
Модуляционный коэффициент ρk и фаза ψ k k-ой гармоники |
|
определяются как |
|
ρk = 2 ak2 + bk2 a0 , ψ k = Arctg(bk ak ), |
(67) |
где ak и bk – амплитуды косинусной и синусной составляющих гармоники:
|
2 |
T |
2 |
T |
|
|||||
ak = |
|
U (t) |
Cos(kΩt)dt, bk = |
|
U (t) |
Sin(kΩt)dt. |
(68) |
|||
T |
T |
|||||||||
|
0 |
|
|
0 |
|
|
|
|||
Обычно в качестве пеленгационной характеристики используют первую гармонику с коэффициентом модуляции, равным в этом случае приближенно:
g = ρ1 |
≈ |
F(θ0 |
− θи ) − F(θ0 |
+ θи) |
(69) |
|
F(θ0 |
− θи) + F(θ0 + θи ) |
|||||
|
|
|
||||
и фазой ψ1 = χи = Ωtи.
Таким образом, при коническом сканировании реализуется аддитивный метод сравнения сигналов, но с последовательной обработкой результатов измерений. К его недостаткам можно отнести общее всем методам одноканального сканирования снижение усиления в равносигнальном направлении, а также потерю части мощности сигнала ошибки при фильтрации первой гармоники.
Из (69) следует, что при обработке сигнала U (t) в методе ска-
нирования смещенным лучом в плоскости, проходящей через равносигнальное направление и направление на источник, образуются «эффективные» разностная и суммарная диаграммы (см. выражение (53):
F = (F(θ0 − θи) − F(θ0 + θи))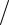
 2 , FΣ = (F(θ0 − θи) + F(θ0 + θи))
2 , FΣ = (F(θ0 − θи) + F(θ0 + θи))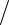
 2 .
2 .
36

Амплитуды этих диаграмм жестко связаны с углом отклонения θ0 сканирующего луча от равносигнального направления, т.е.
имеет место зависимое формирование суммарно-разностных диаграмм.
Подставляя угол θ из выражения (64) и используя симметричную диаграмму направленности (21), получаем
|
F(θ) = F0 exp(μCos(χ − χи)), |
|
μ), |
|
|
|
|
|
|
|
|
|||||||
F |
= exp(−2 ln 2(x2 |
+ x2 )= exp(−0,5(μ + η2 |
|
|
|
|
|
|
|
(70) |
||||||||
0 |
|
0 |
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где η = 4 ln 2x x , μ = 4 ln 2x2 , |
x |
= θ |
0 |
θ |
0,5 |
, x |
= θ |
и |
θ |
0,5 |
. |
|
|
|
|
|||
|
0 и |
|
0 |
0 |
|
|
и |
|
|
|
|
|
|
|
||||
Подставляя (70) в (69), получаем следующее выражение для |
||||||||||||||||||
пеленгационной характеристики: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
exp(η ) − exp(−η ) |
|
|
|
|
|
|
|
θ θ |
|
|
||||||
|
g(η ) = |
|
|
|
|
|
|
|
|
|
4 ln 2 |
0 |
и |
|
(71) |
|||
|
|
|
|
|
|
|
|
|
|
2 |
||||||||
|
exp(η ) + exp(−η ) |
= th(η ) = th |
|
. |
||||||||||||||
|
|
|
|
|
|
|
|
|
θ0,5 |
|
|
|||||||
Пеленгационная чувствительность S в плоскости, проходящей через источник излучения, определяется как
S = |
4 ln 2x |
0 |
|
2 |
2 |
S |
0 |
|
|
|
|
|
|
|
= |
|
, |
(72) |
|||
θ0,5 |
|
|
ch2 (η ) |
|||||||
|
|
exp(η ) + exp(−η ) |
|
|
|
|||||
где S0 = 4 ln 2θ0 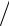 θ02,5 – крутизна пеленгационной характеристики в
θ02,5 – крутизна пеленгационной характеристики в
равносигнальном направлении. Как следует из приведенных формул, они полностью согласуются с соответствующими выражениями для одномерных характеристик.
Параметры сканирующей антенны можно выразить через относительный коэффициент усиления по мощности в равносигнальном направлении, равный относительному уровню мощности в этом направлении:
G0 = G(0) Gmax = exp(−μ) . |
(73) |
Относительный угол отклонения максимума определяется в этом случае как
37
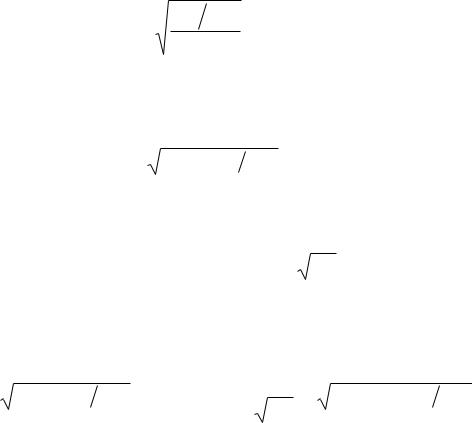
θ0 |
= |
ln(1 G0 ). |
(74) |
|
θ |
||||
|
4 ln 2 |
|
||
0,5 |
|
|
|
Тогда выражение крутизны пеленгационной характеристики в равносигнальном направлении принимает вид
S0 = |
4 ln 2 ln(1 G0 ) |
. |
(75) |
|
|||
|
θ0,5 |
|
|
Важной характеристикой системы является произведение кру- |
|||
тизны S0 на коэффициент усиления G0 или |
G0 = F(0) в равно- |
||
сигнальном направлении. Это произведение характеризует коэффициент использования сигнала и используется при пассивной локации qp и при активной локации qa :
q |
p |
= S G = |
4 ln 2 ln(1 G0 ) |
G , |
q = S |
G = |
4 ln 2G0 ln(1 G0 ) |
. |
|
|
|||||||
|
0 0 |
0 |
a |
0 0 |
θ0,5 |
|||
|
|
|
θ0,5 |
|
|
|||
(76)
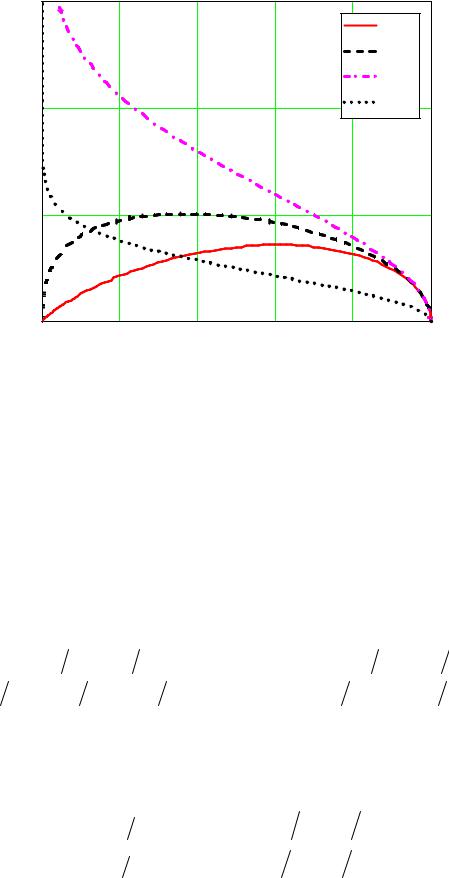
Из представленных соотношений явно прослеживается зависимость эффективности использования энергии сигнала от параметров антенной системы при определении угловых координат источника излучения. На рис. 19 представлены результаты расчетов произведений Qp = q pθ0,5 , Qa = qaθ0,5 и w = S0θ0,5 от коэффици-
ента усиления антенны. Из приведенных зависимостей следует, что qp и qa имеют плавные максимумы в области G0 ≈ 0,6 и
G0 ≈ 0,4 соответственно. Это позволяет выбрать оптимальные значения параметров антенной системы.
38
3 |
|
|
|
Qp |
|
|
|
|
|
|
|
|
|
Qa |
|
|
|
|
w |
2 |
|
|
|
h |
|
|
|
|
|
1 |
|
|
|
|
00 |
0.2 |
0.4 |
0.6 |
0.8 |
|
Коэффициент усиления антенны |
|||
Рис. 19. Нормированные характеристики для сканирующих пеленгационных систем
Напряжение на выходе антенны можно представить, используя разложение (формулы (70)) по степеням показателя экспоненты в виде суммы гармоник
|
|
u(t) = u0 + u1Cos(χ − χи )+ u2Cos2(χ − χи )+ u3Cos3(χ − χи )+ , (77) |
||||||
где u |
0 |
= F |
(1+ η 2 22 + η 4 26 + ), u = F η (1+ η 2 23 + η 4 |
263 + ), |
||||
|
|
|
0 |
1 |
|
0 |
24 + ). |
|
u |
2 |
= F (η 2 |
4)(1+ η 2 223 + η 4 273 + ), u |
3 |
= F (η 3 233)(1+ η 2 |
|||
|
|
|
0 |
|
0 |
|
||
Практически выделение сигнала пеленга по обеим координатам при коническом сканировании осуществляется путем фильтрации первой гармоники
g |
г |
= u Cosχ u |
ηCosχ(1 − η2 |
8 + η4 |
48 − ), |
|
|
|
1 |
0 |
η Sinχ(1 − η2 |
|
48 − ). |
(78) |
|
g |
в |
= u Sinχ u |
8 + η4 |
||||
|
1 |
0 |
|
|
|
|
|
39
Выбор углового и пространственного разноса антенн
Важным параметром антенной системы измерителя углового положения источника является угол смещения максимума относительно равносигнального направления θ0 при амплитудном методе
пеленгования и расстояние между фазовыми центрами антенн при фазовой пеленгации l . Они оказывают существенное влияние на точность определения координат и дальность действия станции. Определение оптимальных значений указанных величин рассмотрим на примере пеленгатора с суммарно-разностным угловым дискриминатором.
Погрешность пеленгования обратно пропорциональна крутизне пеленгационной характеристики и отношению сигнал-шум q :
σ 0 ≡ 1 (S q). |
(79) |
В амплитудной суммарно-разностной системе вблизи равносигнального направления суммарная диаграмма направленности практически неизменна, а разностная – линейна, поэтому
S0 |
|
dg |
dF |
|
FΣ = |
F′(0) |
|
|
||
= |
|
= |
|
|
|
. |
(80) |
|||
dθ |
dθ |
FΣ (0) |
||||||||
|
|
|
|
|
|
|
||||
Оптимальный угол смещения, обеспечивающий максимальную пеленгационную чувствительность, можно было бы найти, решив уравнение
|
d |
|
F′(0) |
= 0, |
(81) |
||
|
|
|
F |
(0) |
|
||
|
|
||||||
|
dθ |
|
|
|
|||
|
|
|
Σ |
|
|
|
|
но из приведенных на рис. 20 значений FΣ (0), F′(0), |
F′(0) FΣ (0) и |
||||||
F′(0)FΣ (0) в зависимости от безразмерного параметра x = θ0 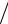 θ0,5 ,
θ0,5 ,
определяемого углом смещения и шириной диаграммы направленности, видно, что отношение F′(0)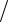 FΣ (0) монотонно возрас-
FΣ (0) монотонно возрас-
тает и в пределах главного лепестка диаграммы направленности не имеет максимума, т.е. не существует оптимального угла сме-
40
