
20060710
.pdf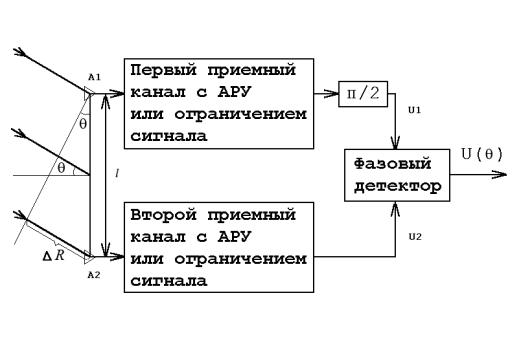
Рис. 11. Фазовый пеленгатор
Напряжение на выходе каждой приемной антенны может быть
представлено в виде: |
)F(θ )exp(i(ωt ± φ / 2)), |
|
|
U |
(t) ~ E(t |
(32) |
|
1,2 |
1,2 |
1,2 |
|
где E(t) – огибающая напряженности поля на раскрыве каждой антенны, φ / 2 = k(R − R1) = k(R2 − R) – набег фазы относительно
центра антенной системы. Поскольку источник достаточно удален от пеленгатора, то можно положить E(t1 ) E(t2 ) и θ1 = θ2 = θ . По-
сле перемножения, фильтрации высокочастотных составляющих и временного усреднения (эти функции выполняет фазовый детектор) получаем:
|
|
|
|
|
|
|
2 |
2πl |
|
|
|
|
u(θ) = pRe(U1U |
|
|
2 |
F |
, |
(33) |
||||||
2 )= pE |
|
|
(θ)Cos |
λ |
Sinθ |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
где сомножитель p характеризует коэффициент преобразования.
Для исключения влияния неизвестной амплитуды вводят эффективную АРУ или ограничение сигнала, благодаря чему напряжение на входе детектора можно считать постоянным. Тогда выражение для u(θ ) можно записать в виде
|
|
l |
|
|
|
|
u(θ ) = u0Cos |
2π |
|
Sinθ |
, |
(34) |
|
λ |
||||||
|
|
|
|
|
где u0 = const.
21
Так как косинус – функция четная, то знак напряжения на выходе фазового детектора не зависит от знака отклонения оси антенны от направления на объект. Для устранения этого недостатка в один из приемных каналов вводят цепь сдвига фазы на π / 2 , вследствие чего зависимость u(θ) приобретает вид дискриминаци-
онной характеристики:
u(θ ) = u Sin |
2π |
l |
Sinθ . |
(35) |
|
|
|||||
0 |
|
|
λ |
|
|
|
|
|
|
|
|
Это позволяет найти пеленгационную характеристику и ее крутизну
|
u(θ ) |
|
|
l |
|
|
g(θ ) = |
u0 |
= Sin |
2π |
|
Sinθ , |
|
λ |
||||||
|
|
|
|
|
l |
|
|
|
|
l |
|
|
|
S(θ) = 2π |
|
Cosθ Cos |
2π |
|
Sinθ . |
(36) |
|||
λ |
λ |
||||||||
|
|
|
|
|
|
|
|||
При малых значениях θ зависимость u(θ) |
имеет приближенно |
||||||||
линейный характер: |
|
|
l |
|
|
|
|
|
|
u(θ ) ≈ u Sin2π |
θ . |
|
|
(37) |
|||||
|
|
|
|||||||
|
|
0 |
λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом, по напряжению на выходе фазового детектора |
|||||||||
можно найти значение и знак угла прихода волны θ. В этом случае пеленгационная характеристика принимает вид
g(θ ) = u(θ ) = 2π |
l |
θ , |
(38) |
|||
λ |
||||||
u |
|
|
|
|
||
0 |
|
|
|
|
|
|
а крутизна пеленгационной характеристики |
|
|||||
S = 2π |
l |
. |
|
|
(39) |
|
|
|
|
||||
|
λ |
|
|
|
||
Результаты расчетов g(θ) и S(θ) по формулам (36) представ-
лены на рис. 12 и 13 при различных значениях соотношения между базой и длиной волны излучения d = l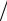 λ .
λ .
22
g
1
0.5 
0
0.5 |
|
|
|
|
d=0,5 |
|
|
|
|
|
d=1 |
|
|
|
|
|
d=2 |
1 |
0.4 |
0.2 |
0 |
0.2 |
0.4 |
|
угол, рад
S
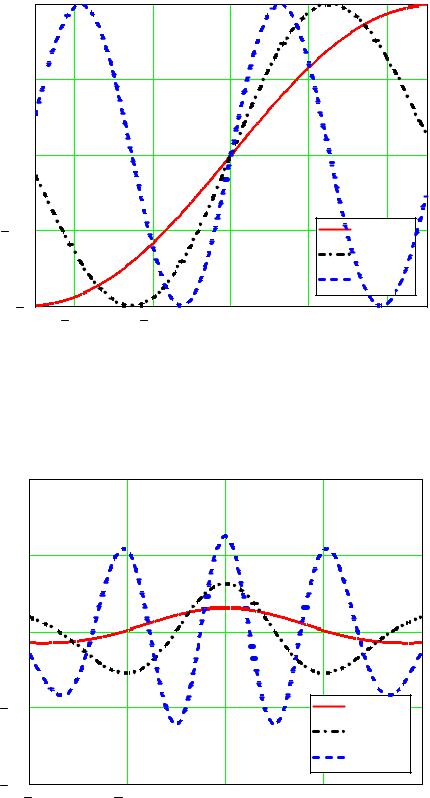
Рис. 12. Пеленгационная характеристика в фазовом методе
20
10 |
|
|
|
|
0 |
|
|
|
|
10 |
|
|
|
d=0,5 |
|
|
|
|
d=1 |
|
|
|
|
d=2 |
20 1 |
0.5 |
0 |
0.5 |
1 |
угол, рад
Рис. 13. Пеленгационная чувствительность в фазовом методе
23

Как следует из приведенных зависимостей, чувствительность, а следовательно, и точность пеленгования растут с увеличением d . Однако при l / λ > 1/ 2 появляется неоднозначность измерения угла, что следует из выражения (36). При диапазоне однозначного измерения разности фаз 2π пределы однозначности измерения углового положения объекта определяются как
θ = λ l . |
(40) |
Это является существенным недостатком фазовых методов пеленгации. Для исключения неоднозначности применяют (так же как в фазовых дальномерных системах) несколько шкал, то есть проводят измерения при различных отношениях l / λ . Необходимо подчеркнуть, что рассмотренный фазовый угломер с ненаправленными антеннами не обладает разрешающей способностью по углу, поскольку два или несколько источников сигнала, расположенных на различных направлениях, создадут в антеннах единый результирующий сигнал (если они неразделимы по другим параметрам), что исключает возможность их раздельного наблюдения и измерения пеленгов. Для разрешения сигналов по углу необходимы антенны с достаточно узкой амплитудной характеристикой направленности. Существенным недостатком рассмотренного типа фазового пеленгатора является также зависимость пеленгационной характеристики и точности измерения угловых координат от фазовых характеристик трактов, которые зачастую нестабильны.
Этот недостаток простых фазовых пеленгаторов устраняется в схемах с суммарно-разностной обработкой. В этом случае на вхо-
ды фазового детектора подаются суммарный и разностный сигналы, принимаемые двумя пространственно-разнесенными антеннами, как представлено на рис. 11. В данном случае, с учетом
E(t1 ) E(t2 ), θ1 = θ2 = θ и фазовращателя на π 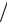 2 , они могут быть представлены как
2 , они могут быть представлены как
U (t) ~ E(t)F(θ )(exp(i(ωt + π 2 − |
φ / 2))− exp(i(ωt + |
φ / 2))), (41) |
|||||||
UΣ (t) ~ E(t)F(θ )(exp(i(ωt + π 2 − |
φ / 2))+ exp(i(ωt + |
φ / 2))). (42) |
|||||||
Тогда осуществляя операции, аналогичные тем, которые были |
|||||||||
сделаны для метода изложенного выше, получим: |
|
||||||||
|
|
|
|
|
|
2 |
2πl |
|
|
|
|
|
2 |
F |
(43) |
||||
u(θ) = pRe(U UΣ )= pE |
|
|
(θ)Sin |
Sinθ . |
|||||
|
|
|
|
|
|
|
λ |
|
|
24
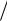
Вводя АРУ или ограничение сигналов, получим следующее выражение:
u(θ) = u Sin |
2π |
l |
Sinθ |
|
, |
(44) |
|
|
|||||||
0 |
|
|
λ |
|
|
|
|
|
|
|
|
|
|
|
|
которое полностью совпадает с (36). Поэтому характеристики пеленгационной чувствительности и ее крутизны – такие же, как на рис. 12 и 13. Однако в данном случае пеленгационное направление θ не зависит от стабильности и точности установки амплитудных и фазовых параметров каналов в отличие от простой фазоразностной схемы.
В отдельных случаях фазовый метод можно применять с обра-
боткой в схеме сравнения амплитуд разностного и суммарного ка-
налов на видеочастоте. В этом случае определяя отношение разности и суммы сигналов (41), (42) со сдвигом фазы на π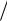 2 в одном из
2 в одном из
каналов (например разностном) и выполняя усреднение, получим
|
|
|
|
|
|
|
|
φ |
|
|
|
l |
|
|
|
|
||
u(θ) = Re |
U |
|
|
= tg |
|
= tg |
|
π |
Sinθ |
|
. |
(45) |
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|||||||||||||||
|
|
|
|
|
2 |
|
|
λ |
|
|
|
|||||||
|
U |
Σ |
|
|
|
|
|
|
|
|
|
|
||||||
Тогда выражения для пеленгационной характеристики и пеленгационной чувствительности принимают следующий вид:
|
|
l |
|
|
|
|
l |
|
|
|
l |
−2 |
||
u(θ) = tg |
π |
|
Sinθ |
, |
S0 |
= π |
|
Cosθ Cos |
π |
|
Sinθ |
. (46) |
||
λ |
λ |
λ |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
Графики зависимости вышеприведенных характеристик представлены на рис. 14 и 15.
Пеленгационная характеристика является нечетной функцией, а ее крутизна – четной функцией угла смещения источника. При расположении последнего в равносигнальном направлении пеленгационная чувствительность определяется соотношением размера базы к длине волны излучения d = l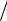 λ . Однако в отличие от предыдущих
λ . Однако в отличие от предыдущих
двух методов диапазон неоднозначности определяется как
θ = λ 2l . |
(47) |
25
|
40 |
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
g |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
d=0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d=1 |
|
|
|
|
|
|
|
|
d=1,5 |
|
|
40 |
3 |
2 |
1 |
0 |
1 |
2 |
3 |
|
|
|
|
|
угол, рад |
|
|
|
|
|
|
Рис. 14. Пеленгационная характеристика |
|
||||
в фазовом методе с суммарно-разностной обработкой амплитуд |
||||||||
|
300 |
|
|
|
|
|
|
|
|
200 |
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
S |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
200 |
|
|
|
|
|
d=0,5 |
|
|
|
|
|
|
|
d=1,0 |
|
|
|
|
|
|
|
|
|
d=1,5 |
|
|
300 |
3 |
2 |
1 |
0 |
1 |
2 |
3 |
|
|
|
|
|
угол, рад |
|
|
|
|
|
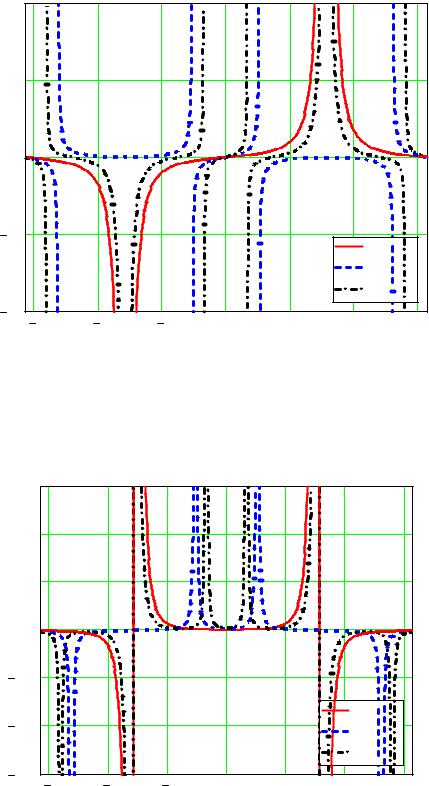
Рис. 15. Пеленгационная чувствительность |
|
|||||
в фазовом методе с суммарно-разностной обработкой амплитуд |
||||||||
26
Кроме рассмотренных выше схем измерения углового положения источника, получили распространение также фазовые радиопеленгаторы, в которых изменение фазы сигнала вызвано эффектом Доплера. Простейший пеленгатор такого типа имеет ненаправленную в горизонтальной плоскости антенну A1 , которая дви-
жется с угловой скоростью Ω по окружности радиусом Dr 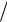 2 вокруг центральной антенны A2 . Поскольку при движении антенны
2 вокруг центральной антенны A2 . Поскольку при движении антенны
ее расстояние до источника излучения меняется с периодом 2π / Ω , возникает эффект Доплера, вызывающий фазовую модуляцию ЭДС, наводимой в антенне A1 по закону
eA1 = ESin(ωt + mϕ cos(Ωt − θ)), |
(48) |
где mϕ = πDr / λ − индекс фазовой модуляции; θ – угол на источ-
ник.
Таким образом, информация о пеленге заключена в фазе модулирующего колебания, которое может быть выделено при сравнении сигнала антенн A1 и A2 в фазовом детекторе.
При больших диаметрах Dr вращение антенн A1 с требуемой
угловой скоростью затруднительно и вместо одной движущейся антенны несколько неподвижных антенн располагается на окружности диаметром Dr и поочередно подключаются к входу прием-
ника пеленгатора. В этом случае непрерывная модуляционная функция заменяется рядом ее дискретных значений. На основе теоремы Котельникова для точного воспроизведения непрерывной функции расстояние l1 между соседними антеннами, расположен-
ными по окружности, не должно превышать половины длины волны несущих колебаний принимаемого сигнала.
Применение эффекта Доплера возможно и в радиомаяках, в которых с помощью вращающейся антенны или ряда неподвижных коммутируемых антенн фаза излучаемого сигнала модулируется, и параметры модуляции несут информацию об обратном пеленге объекта, извлекаемую при обработке сигнала, принимаемого на объекте.
При увеличении диаметра Dr пропорционально растет девиа-
ция частоты излучаемых доплеровским маяком колебаний, что позволяет повысить помехоустойчивость системы и, в частности,
27

уменьшить влияние на точность пеленгования отражений от местных предметов.
Структурные схемы радиопеленгаторов
Рассмотрим схемы построения пеленгаторов с общей точки зрения. Диаграммы направленности антенной системы, которые являются комплексными функциями угла прихода, выражаются зависимостями:
f |
(θ) = F |
(θ) exp(iΦ (θ)), |
f |
(θ) = F (θ) exp(iΦ |
2 |
(θ)) . |
(49) |
1 |
1 |
1 |
2 |
2 |
|
|
Таким образом, в любой системе сравниваются сигналы, соответствующие двум последовательным состояниям одной антенны или двум лучам антенной системы:
U |
(t) ~ E(t) f |
(θ) , U |
2 |
(t) ~ E(t) f |
(θ) , |
(50) |
1 |
1 |
|
2 |
|
|
где θ — координата источника, отсчитываемая от оси пеленгатора.
Сигналы U |
и U |
2 |
зависят от расстояния до источника. |
Метод |
||||
1 |
|
|
|
|
|
|
|
|
сравнения позволяет эту зависимость исключить. |
|
|||||||
Запишем отношение двух принятых сигналов |
|
|||||||
|
r |
(θ) = U |
(t) U |
2 |
(t) = f (θ) |
f (θ) . |
(51) |
|
|
|
m |
1 |
|
1 |
2 |
|
|
Данное отношение, которое в дальнейшем будем называть мультипликативным, при определенных условиях может служить исходным для формирования пеленгационной характеристики и получения информации об угловом положении источника излучения.
Кроме того, для формирования пеленгационной характеристики может быть использовано также отношение разностного сигнала к суммарному:
|
U |
(t, θ) − U |
2 |
(t, θ) |
|
f |
(θ) − f |
(θ) |
|
f |
(θ) |
|
|
r (θ) = |
1 |
|
|
= |
1 |
2 |
|
= |
|
|
, |
(52) |
|
U |
(t, θ) + U |
|
(t, θ) |
f |
(θ) + f |
(θ) |
f |
(θ) |
|||||
a |
2 |
|
|
|
|
||||||||
|
1 |
|
|
|
1 |
2 |
|
|
Σ |
|
|
||
которое обычно называют аддитивным отношением принятых сигналов. В отношение (52) входят так называемые суммарные и
разностные диаграммы fΣ (θ ) и f (θ ) . С учетом нормирующего
множителя, обеспечивающего баланс мощности в двух представлениях, получаем
f |
(θ) = ( f |
(θ) + f |
(θ)) |
2 , f |
(θ) = ( f |
(θ) − f |
(θ)) |
2 , |
(53) |
Σ |
1 |
2 |
|
|
1 |
2 |
|
|
|
28

и, наоборот,
f1(θ) = ( fΣ (θ) + f (θ))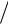
 2 , f2 (θ) = ( fΣ (θ) − f (θ))
2 , f2 (θ) = ( fΣ (θ) − f (θ))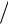
 2 . (54)
2 . (54)
Отметим, что разностная диаграмма в (52) и (53) может быть организована и вычитанием первого сигнала из второго, т.е. иметь противоположный знак, что не имеет принципиального значения.
Связь между мультипликативными и аддитивными отношениями сигналов устанавливается с помощью следующих выражений:
r |
(θ ) = rm (θ ) − 1 |
, |
r |
(θ ) = 1 |
+ ra (θ ) . |
(55) |
a |
|
|
m |
1 |
|
|
|
rm (θ ) + 1 |
|
|
− ra (θ ) |
|
Диаграммы f1(θ ) и f2 (θ ) должны отвечать определенным
условиям. На оси пеленгатора (θ = 0) сигналы должны быть одинаковыми, следовательно, выполняются условия:
ra (θ = 0) = 0, rm (θ = 0) = 1. |
(56) |
Поэтому это направление (θ = 0) называется равносигнальным |
|
направлением радиопеленгатора. |
|
Пеленгационная характеристика угломерной системы должна |
|
быть нечетной действительной функцией угла прихода θ |
[1]. От- |
сюда отношение принятых сигналов должно меняться на обратное при перемещении источника в симметричную относительно оси пеленгатора точку. Для мультипликативного и аддитивного отношений это соответствует условиям:
rm (θ ) = 1 rm (−θ ) , ra (θ ) = −ra (−θ ) . |
(57) |
Очевидно, что соотношения (57) удовлетворяются для случая диаграмм, обладающих зеркальной симметрией относительно равносигнального направления, максимумы которых смещены от оси на ± θ0 :
F1(θ) = F(θ0 − θ), F2 (θ) = F(θ0 + θ), Φ1(θ) = −Φ2 (θ) = Φ(θ)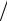 2 . (58)
2 . (58)
Из-за зеркальной симметрии диаграмм f1(θ ) и f2 (θ ) суммарная диаграмма fΣ (θ ) имеет четную симметрию относительно равносигнального направления, а разностная f (θ ) – нечетную.
Кроме мультипликативного и аддитивного отношений могут быть образованы другие отношения, удовлетворяющие требованиям, предъявляемым к пеленгационной характеристике радиопеленгатора. При умножении мультипликативного и аддитивного
отношений на комплексную постоянную b
29
b = b exp(iψ )
получим линейно-преобразованные отношения
r |
(θ ) = br |
(θ ), |
r |
(θ ) = br |
(θ ), |
(59) |
a |
a |
|
m |
m |
|
|
которые могут быть использованы для определения углового положения источника излучения.
Устройства, в которых образуются сумма и разность принятых сигналов или производится операция умножения принятых
сигналов на коэффициент b, называются преобразователями, так как в них в общем случае возможно преобразование информации из амплитудных соотношений в фазовые и обратно. Эти преобразования осуществляются обычно на высокой частоте с использованием пассивных элементов в виде мостовых соединений, отрезков линий и т.п. из-за их относительной простоты и стабильности характеристик [4].
Операцию вычисления отношения двух сигналов, преобразованных или непреобразованных, невозможно выполнить без предварительного их усиления. Устройство, содержащее активные элементы, включая усилители и схему сравнения, которое выделяет мультипликативное или аддитивное отношение и образует пеленгационную характеристику, называется угловым дискриминатором.
Для каждого вида отношений (51) и (52) возможны три метода пеленгации – амплитудный, фазовый и комплексный (ампли- тудно-фазовый). При амплитудном пеленговании угловая информация содержится в амплитудных диаграммах F1(θ ) и F2 (θ ). В
этом случае при идентичных фазовых диаграммах мультипликативное и аддитивное отношение выражаются только через амплитудные диаграммы направленности
rm (θ ) = |
|
F1 |
(θ ) |
= |
F(θ0 |
− θ ) |
= ρ (θ ), |
|
||||
|
F2 |
(θ ) |
F(θ0 |
+ θ ) |
(60) |
|||||||
|
|
|
|
|
|
|
||||||
|
F1(θ ) − F2 |
(θ ) |
|
F (θ ) |
|
|||||||
ra (θ ) = |
= |
= ρa (θ ). |
|
|||||||||
F1 |
(θ ) + F2 |
(θ ) |
FΣ (θ ) |
|
||||||||
|
|
|
|
|||||||||
При фазовом пеленговании, когда амплитудные диаграммы идентичны, угловая информация содержится в разности фаз
ΔΦ(θ ) = Φ1(θ ) − Φ2 (θ ) . |
(61) |
30
