
Цос экзамен ответы
.pdf
линии задержки полоса пропускания фазорасщепителя по выходу синусной компоненты расширяется, а АЧХ приближается к АЧХ по выходу косинусной компоненты.
1.11
K |
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
s |
|
0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
|
|
|
|
|
||||
|
|
|
|
0 |
|
|
|
Рисунок 3.2 – АЧХ фазорасщепителя на двух элементах задержки
1.11
K |
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
s |
|
0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
|
|
|
|
|
||||
|
|
|
|
0 |
|
|
|
Рисунок 3.3 – АЧХ фазорасщепителя на шести элементах задержки
Дальнейшее увеличение длины линии задержки приближает АЧХ по выходу косинусной компоненты к идеальной АЧХ по выходу синусной компоненты, однако на границах интервала Котельникова коэффициент передачи по выходу синусной компоненты всегда равен нулю, что следует из (3.1).
Таким образом, реальный нерекурсивный ФР отличается от идеального амплитудной погрешностью, которую можно уменьшить за счет увеличения длины линии задержки и оптимального выбора коэффициентов B2m+1.
Всепропускающая цифровая цепь
На рисунке 3.4 показана цифровая цепь первого порядка, содержащая как рекурсивную, так и нерекурсивную части.
xn |
vn |
a yn
z-1
- a
Рисунок 3.4 – Всепропускающая цифровая цепь
Ее системная функция описывается следующим соотношением
H(z) a z 1 . 1 az 1
- 3 -
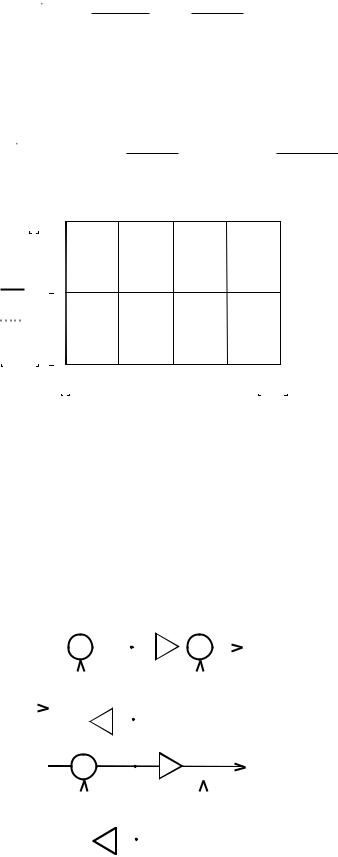
Особенностью этой цепочки является равенство коэффициентов, определяющих свойства рекурсивной и нерекурсивной частей фильтра.
Определим комплексный коэффициент передачи, воспользовавшись подстановкой
|
|
z e |
j |
|
|
|
|
||
|
|
|
|
|
|
|
|||
|
a e |
j |
|
|
1 ae |
j |
|||
|
|
|
|
j |
|
||||
K( j ) |
|
|
|
|
e |
|
j . |
||
1 |
a e |
j |
|
1 ae |
|||||
|
|
|
|
|
|
||||
Из последнего соотношения следует, что модуль комплексного коэффициента передачи равен единице при любых значениях . Именно поэтому данная цифровая цепь называется всепропускающей.
Определим ФЧХ цепи
|
|
1 ae |
j |
|
j |
|
|||
( ) arg(K( j )) arg e |
|
|
|
|
|
1 ae |
j |
||
|
|
|
|
|
|
2arctg |
a sin |
|
|
|
|
1 |
a cos |
.
На рисунке 3.5 показаны две ФЧХ при разных значениях коэффициента а.
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
3.142 |
4 |
|
|
|
|
|
||
|
|
|
0 |
1 |
2 |
3 |
4 |
|
|
|
|
|
|||||
|
|
|
|
0 |
|
|
|
3.142 |
Рисунок 3.5 – ФЧХ всепропускающих цепей при а = 0.5 (
1( )
) и а = -0.5 (
|
( ) |
2 |
|
)
Обе цепочки имеют нулевой фазовый сдвиг при |
=0 и фазовый сдвиг при |
= |
. Однако на других частотах они расходятся так, что в ограниченном частотном диапазоне существует примерно постоянная разность фазовых сдвигов, вносимых ими. Это позволяет использовать всепропускающие цепи для построения рекурсивных фазорасщепителей.
Рекурсивный 90 – градусный фазорасщепитель |
|
На рисунке 3.6 показан фазорасщепитель, выполненный на двух |
|
всепропускающих цепях, имеющих общий вход (рисунок 3.6). |
|
a |
yan |
z-1 |
|
xn
- a
b  ybn
ybn
z-1
- b
Рисунок 3.6 – 90-градусный фазорасщепитель
- 4 -

Комплексные коэффициенты передачи двух всепропускающих цепей, образующих ФР, определяются следующими соотношениями
|
|
a e |
j |
|
|
|
|
b e |
j |
||
K |
( j ) |
|
|
, |
K |
|
( j ) |
|
|
||
|
|
j |
b |
|
|
j |
|||||
a |
|
1 a e |
|
|
|
1 be |
|||||
|
|
|
|
|
|
|
|
||||
.
Определим разность фазовых сдвигов, вносимых всепропускающими цепями
|
K |
( j ) |
|
(a e j )(1 be j ) |
||||||
( ) arg |
a |
|
|
arg |
|
|
|
|
|
. |
|
|
(1 a e |
j |
)(b e |
j |
|
||||
Kb ( j ) |
|
|
|
) |
||||||
Умножив числитель и знаменатель дроби под знаком аргумента на ej , получим
|
(a e j )(b ej ) |
2arg((a e j )(b ej )) 2arctg |
csin |
, |
|||||
( ) arg |
|
|
|
|
|
|
|
||
(a e |
j |
)(b e |
j |
|
1 d cos |
||||
|
|
|
) |
|
|
||||
где |
с |
a b |
, |
d |
a b |
||
1 ab |
1 |
ab |
|||||
|
|
|
|
||||
Экстремум функции |
( ) |
||||||
.
имеет место при выполнении условия
cos( 0 )
Экстремальное значение функции равно
d
.
( ) 2arctg |
|
c |
|
|
|
0 |
1 |
d |
|
|
2 |
.
При наличии одной точки экстремума для абсолютной величине отклонений ( ) от требуемого выполнить два условия:
( g1 ) ( g2 ) , |
( ) |
|
0 |
||
|
||
|
2 |
получения |
равновеликих по |
значения 0 |
2 необходимо |
( |
g1 |
) |
0 |
, |
|
|
|||
|
|
|
|
где g1 |
и g2 - нижняя и верхняя границы расчетного интервала. |
|
Из первого условия находится константа |
|
cos |
|
g1 |
|
g2 |
|
|
|
|||
|
|
|
2 |
|
|
d |
|
|
|
. |
|
|
|
|
|
||
|
cos |
g1 |
g2 |
||
|
|
|
|||
|
|
|
2 |
|
|
|
|
|
|
|
Второе условие приводит к трансцендентному уравнению, позволяющему определить константу с
|
c |
|
|
csin |
arctg |
|
|
arctg |
g1 |
d |
|
d cos g1 |
||
1 |
2 |
1 |
||
|
|
|
|
|
0 |
|
.
По известным коэффициентам с и d находятся коэффициенты системной функции
|
|
|
|
|
|
|
a |
1 1 c2 d2 |
, |
b |
a c |
. |
|
|
|
|
||||
|
c d |
|
|
1 a c |
||
На рисунке 3.7 приведена зависимость фазового сдвига между выходными сигналами ФР при g1  18 и g2 2
18 и g2 2  3 .
3 .
- 5 -

1.983 |
2 |
|
1.5
2
1.158 |
1 |
|
|
|
|
0 |
1 |
2 |
|
|
|
|||
|
|
0.175 |
|
2.5 |
Рисунок 3.7 – Зависимость фазового сдвига между выходными сигналами ФР, содержащего по одной всепропускающей цепи в каждой ветви
Из него видно, что фазовая погрешность имеет равновеликие пульсации в заданном диапазоне частот. Максимальная величина погрешности составляет 26%. Для уменьшения погрешности нужно увеличивать количество всепропускающих цепочек.
На рисунке 3.8 показаны зависимости фазового сдвига между выходными сигналами фазорасщепителей, содержащих по 2 (а) и по 3 (б) фазосдвигающих цепи в
каждой ветви. В интервале от |
g1 18 |
до |
g2 |
2 3 |
|
погрешности менее 3% и 0.3% соответственно. |
|
|
|||
1.65 |
|
|
|
|
|
1.6 |
|
|
|
|
|
|
|
|
|
|
|
1.55 |
|
|
|
|
|
1.5 |
0 |
0.5 |
1 |
|
1.5 |
|
|
||||
|
|
|
|
|
|
максимальные фазовые
a)
2 |
2.5 |
б)
|
1.57 |
|
|
|
|
|
|
|
1.56 |
0 |
0.5 |
1 |
1.5 |
2 |
2.5 |
|
|
||||||
|
|
|
|
|
|
|
|
Рисунок 3.8 - Зависимости фазового сдвига между выходными сигналами ФР, содержащих по 2 (а) и по 3 (б) всепропускающих цепи в каждой
ветви
Применение всепропускающих цепей для построения рекурсивного ФР обеспечивает отсутствие у этих ФР амплитудной погрешности.
Генераторы пилообразных, прямоугольных, треугольных и трапецеидальных колебаний
На рисунке 3.9 точками показаны отсчеты пилообразного колебания, которое при A>0 формируется следующим образом:
- 6 -

|
|
z((n 1)T |
) A |
при |
z((n 1)T |
) A P, |
|
z(nT |
) |
|
Д |
|
|
Д |
|
|
|
|
|
|
|
||
Д |
|
z((n 1)T |
) A 2P |
при |
z((n 1)T |
) A P. |
|
|
|
|
|||||
|
|
Д |
|
|
Д |
|
|
|
|
|
|
|
|
|
|
Записанное соотношение справедливо в дискретные моменты времени.
Если рассматривать не дискретные моменты времени, а порядковые номера отсчетов, то это соотношение можно записать так
zn |
z |
n 1 |
A |
при |
z |
n 1 |
A P, |
|
|
|
|
|
|||
|
|
|
zn 1 |
|
|||
|
zn 1 |
A 2P |
при |
A P. |
|||
z(nT |
) |
Д |
|
P |
|
A |
|
nTД
- P |
Tд |
|
T |
||
|
Рисунок 3.9 – Пилообразное колебание
Из рисунка видно, что в периоде пилообразного колебания
интервалов дискретизации, следовательно, период T и частота колебания равны
содержится |
2P A |
F пилообразного
T |
2P |
T , |
F |
A |
F . |
|
|
||||
|
A Д |
|
2P Д |
||
Частота пилы прямо пропорциональна частоте дискретизации и отношению констант A P .
P .
Рисунок 3.10 показывает, как из пилообразного колебания z получается последовательность прямоугольных импульсов I с периодом, равным периоду пилы, длительностью , максимальным уровнем I1, минимальным уровнем I2
|
|
|
|
|
|
|
|
|
|
I |
при |
z |
n |
C, |
|||
|
|
|
|
|
In |
|
1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
zn |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
I2 |
при |
C. |
|||||
z |
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
||
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
-P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
I1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t
I2
- 7 -

Рисунок 3.10 – Формирование последовательности прямоугольных импульсов из пилообразного колебания
Из подобия заштрихованного треугольника и треугольника - положительного полупериода пилы следует что
|
|
P C |
. |
T |
|
||
2 |
P |
|
Откуда длительность импульса равна
T 1 C .
2 P
Таким образом, изменяя константу С, можно регулировать длительность импульса.
Из пилы формируется треугольное колебание (рисунок 3.11) в соответствии со следующим соотношением
Y  z
z P
P 2.
2.
Это двухполярное треугольное колебание может быть использовано в качестве грубой аппроксимации синусоиды. Степень соответствия его синусоиде можно оценить по уровню высших гармоник в спектре этого колебания. Спектр содержит только нечетные гармоники, причем коэффициент третьей гармоники равен кГ3 = 10%, а коэффициент пятой гармоники кГ5 = 4%.
Из треугольного колебания формируется трапецеидальное колебание согласно соотношению
|
|
BY |
при |
P BY P, |
|||||||
|
|
|
|
|
n |
|
|
|
n |
||
T |
|
P |
|
при |
BY |
|
P, |
||||
|
|
|
|||||||||
p n |
|
|
|
|
|
n |
|
|
|
||
|
|
|
P |
|
при |
BY P, |
|||||
|
|
|
|
||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
где B > 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|||
|
|
-P |
|
|
|
|
|
|
|
||
|
|
P |
|
|
|
|
|
|
z |
||
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
Y |
|
|
|
|
|
|
|||
|
|
|
|
z |
-P/2 |
||||||
|
|
P/2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||
|
|
0 |
|
|
|
|
|
|
|
t |
|
|
-P/2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
Рисунок 3.11 – Формирование треугольных колебаний
- 8 -

Y |
|
P/2 |
|
0 |
t |
-P/2 |
|
|
BY |
P |
Tp |
|
|
0 |
t |
|
|
- P |
|
Рисунок 3.12 – Формирование трапецеидального колебания
При B = 3 трапеция является хорошей аппроксимацией синусоиды: коэффициент третьей гармоники равен нулю, коэффициент пятой гармоники кГ5 = 4%.
Косинусно-синусные генераторы. Косинусно-синусный генератор с полиномиальной аппроксимацией отсчетов выходных колебаний
Для формирования двух квадратурных компонент на выходе генератора используются два пилообразных колебания, сдвинутых друг относительно друга на четверть периода (рисунок 3.13). Исходным является одно из пилообразных колебаний при P=1 (в рассматриваемом случае zc). Второе получается из него следующим образом
|
zc n 0.5 |
при |
zc n 0.5 1, |
|
zs n |
|
|
|
|
|
|
|
zc n 0.5 1. |
|
|
zc n |
1.5 |
при |
|
|
|
|
|
|
Из двух пилообразных колебаний формируются два треугольных описанным выше способом
Y |
0.5 z |
cn |
, |
Y |
z |
sn |
0.5. |
c n |
|
|
s n |
|
|
- 9 -

zc |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
t |
zs |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
t |
-1 |
|
|
|
|
|
|
|
|
1 |
|
Y |
|
= 0.5- z |
|
|||
0.5 |
|
c |
c |
|||||
|
|
|
|
|
|
|||
0 |
|
|
|
|
|
|
|
t |
-0.5 |
|
|
|
|
C |
|
||
|
|
|
|
|
|
|||
-1 |
|
|
|
|
|
|
|
|
0. - |
|
|
|
|
|
|
|
|
1 |
|
Y = |
z |
|
-0.5 |
|||
|
S |
s |
||||||
0.5 |
|
|
s |
|
|
|
||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
-0.5 |
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
Рисунок 3.13 – Формирование косинусной и синусной компонент из двух пилообразных колебаний
Для формирования из треугольных колебаний синусоидальных используется функциональное преобразование F(Y), представляющее собой полином третьей или пятой степени:
|
|
2 |
), |
|
F(Y) 4Y(D Y |
||
где D = 0.70738, F(Y) 4Y(D 4Y2 |
(D D Y2 )), где D1= 0.745966, D3 = - 0.305500, D5 |
||
1 |
3 |
5 |
|
= 0.138149.
Отсчёты генерируемых колебаний определяются следующим образом:
Cn F(Yc n ), Sn F(Ys n ).
При использовании полинома третьей степени коэффициент третьей гармоники равен кГ3 = 0.5%, коэффициент пятой гармоники кГ5 = 0.1%.
При использовании полинома пятой степени кГ3 =0.005%, кГ5 = 0.005%.
Для дальнейшего уменьшения коэффициентов гармоник используются полиномы более высокого порядка [3].
Косинусно-синусный генератор с табличной организацией отсчетов
|
выходных колебаний |
|
Функция sin(π z) при |
1 z 1 |
преобразует пилообразное колебание в |
синусоидальное (рисунок 3.14). Реализуется такой генератор путем записи табличных значений этой функции в постоянное запоминающее устройство (ПЗУ). Аргумент функции задает адрес ячейки, в которой хранится значение функции. Шаг изменения
аргумента равен 1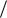 2m 1 , где m-количество разрядов адреса ПЗУ. Косинусную компоненту можно получить двумя способами:
2m 1 , где m-количество разрядов адреса ПЗУ. Косинусную компоненту можно получить двумя способами:
- 10 -

c помощью функции cos(π z) и той же пилы, которая используется для формирования синусной компоненты;
c использованием только одной функции и двух пилообразных колебаний, сдвинутых друг относительно друга на четверть периода.
|
1 |
sin(πz) |
|
1 |
|
|
-1 |
|
0 |
1 |
z |
0 |
t |
-1 |
-0.5 0 |
0.5 |
1 |
|
z |
|
t 
Рисунок 3.14 – Формирование синусоидального колебания с использованием заданной таблично функции sin(πz)
Преобразователи частоты
Преобразователь частоты предназначен для переноса спектра входного сигнала из одной области частот в другую без изменения формы спектра.
На рисунке 3.15 показан преобразователь частоты, содержащий перемножитель, генератор синусоидальных колебаний Г и фильтр.
x |
v |
|
wn |
|
n |
n |
Фильтр |
||
|
||||
|
|
|
||
|
x |
|
|
|
|
Гn |
|
|
|
|
Г |
|
|
Рисунок 3.15 – Преобразователь частоты с выходным фильтром
Пусть сигнал на входе преобразователя описывается соотношением
x |
n |
X |
cos( nT |
|
), |
|
n |
Д |
n |
|
где Xn и φn – изменяющиеся во времени амплитуда и фаза входного сигнала соответственно, ω – частота сигнала.
Пусть на выходе генератора действует колебание вида
x |
Гn |
X |
Г |
cos( nT ), |
|
|
Г Д |
где XГ – постоянная амплитуда, ωГ – частота генерируемого колебания. На выходе перемножителя действует сигнал
vn 12 XnXГ cos(( Г )nTД n ) 12 XnXГ cos(( Г )nTД n ).
Если частотой выходного сигнала преобразователя является частота ω – ωГ, то первое слагаемое описывает полезный продукт преобразования, а второе – побочный. Для удаления побочного продукта преобразования можно использовать или полосовой
- 11 -
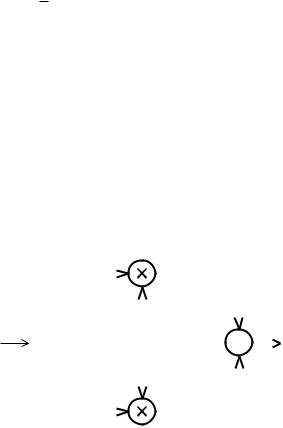
фильтр с центральной частотой полосы пропускания, равной ω – ωГ, или ФНЧ, подавляющий составляющую частоты ω + ωГ.
Поэтому выходной сигнал преобразователя равен
w |
|
|
1 |
X |
X |
K |
|
cos(( )nT |
|
|
|
|
), |
|
n |
|
Ф |
n |
|
||||||||||
|
|
2 |
n |
Г |
|
Г |
Д |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где KФ – коэффициент передачи фильтра для полезного продукта преобразования,
-
постоянный фазовый сдвиг, вносимый фильтром на частоте
Г
. Полученное
соотношение справедливо, если коэффициент передачи фильтра для побочного продукта преобразования равен нулю. В противном случае на выходе преобразователя будет действовать ослабленная составляющая на частоте ω + ωГ.
Из последнего соотношения видно, что изменяющиеся во времени амплитуда и фаза выходного сигнала преобразователя частоты связаны линейными соотношениями с амплитудой и фазой входного сигнала. Это означает, что преобразование частоты не изменяет закона модуляции как при амплитудной, так и при угловой модуляции.
На рисунке 3.16 приведена схема квадратурного преобразователя частоты, содержащего 90-градусный фазорасщепитель и косинусно-синусный генератор.
x |
cn |
|
C |
|
|
n |
|
|
ФР |
КСГ |
W |
|
n |
||
|
|
|
|
|
/2 |
|
|
x sn |
|
Sn |
|
Рисунок 3.16 – Квадратурный преобразователь частоты Пусть на выходах фазоращепителя действуют две квадратурные составляющие
входного сигнала
x |
cn |
X |
cos( nT |
|
), |
x |
sn |
X |
sin( nT |
|
). |
|
n |
Д |
n |
|
|
n |
Д |
n |
|
Пусть на выходах косинусно-синусного генератора существуют колебания
C |
X |
Г |
cos( nT ), |
S |
X |
Г |
sin( nT |
). |
n |
|
Г Д |
n |
|
Г Д |
|
Тогда выходной сигнал преобразователя определится соотношением wn XnXГ cos(( Г )nTД n ).
Таким образом, в случае идеальных ФР и КСГ на выходе преобразователя получается только полезный продукт преобразования. При наличии погрешностей этих узлов наряду с полезным продуктом преобразования будет существовать ослабленный побочный продукт преобразования.
- 12 -
