Готовые РГР / Расчетно-графическая работа Вариант 4

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕ- ДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение высшего образования

«Казанский национальный исследовательский технический университет им. А.Н. Туполева-КАИ»

Институт Радиоэлектроники, фотоники и цифровых технологий

(наименование института (факультета), филиала)

Кафедра Радиофотоники и микроволновых технологий

(наименование кафедры)

11.03.02 «Инфокоммуникационные технологии и системы связи»

(шифр и наименование направления подготовки (специальности))

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА

по дисциплине

«Цифровая обработка сигналов» Вариант 4

Обучающийся
	(номер группы)	(подпись, дата)	№ зачет.кн.	(Ф.И.О.)
Руководитель	Доцент РФМТ		Р.Р. Самигуллин
	(должность)		(Ф.И.О.)

Казань, 2022

Содержание

Задание №1. 3

Решение 4

Задание №2. 8

Решение 9

Задание №3. 11

Решение 12

Задание №1.

Моделирование процесса дискретизации аналогового сигнала и восстановления ана- логового сигнала из дискретного.

Наблюдение эффектов размножения и наложения спектров Требуется:

1. Сформировать аналоговый сигнал ^x(t) в виде суммы трех гармонических колебаний

где

x(t)  x₁(t)  x₂ (t)  x₃ (t),

x₁ (t)  X₁ cos(2  F₁t  ₁ ), x₂ (t)  X₂ cos(2  F₂ t  ₂ ), x₃ (t)  X₃ cos(2  F₃t  ₃ ), F₂ =2 F₁, F₃ = 3 F₁.

(1)

При моделировании аналогового сигнала на ЭВМ следует принять

t it,

где ^t - временной интервал между двумя соседними расчетными точками, i – порядковый номер расчетной точки, изменяющийся от 0 до i_max.

Значения X₁, X₂, X₃, φ₁, φ_2, φ₃, F₁ и Δt приведены в таблице 1.

Таблица 1. Исходные данные для выполнения задания №1

Номер варианта- -последняя цифра номера студенческого билета	X1	X2	X3	φ1	φ 2	φ 3	F1	FД	Δt
4	1	0.5	0	0	0	0	1кГц	8кГц	1/512 мс

2. Определить амплитудный спектр аналогового сигнала.

3. Сформировать вспомогательный сигнал ^u(t) в виде периодической последователь-

ности единичных отсчетов с периодом, равным интервалу дискретизации T  ¹ , где

F

Д

Д

F_Д – частота дискретизации (рисунок 1). Значение F_Д приведено в таблице 1.

₀ t

Рисунок 1 – Вспомогательный сигнал в виде последовательности единичных отсчетов

4. Сформировать дискретный сигнал

x_d (t)  x(t) u(t) _.

5. Определить амплитудные спектры аналогового и дискретного сигналов и убедиться в том, что при дискретизации имеет место эффект размножения спектра аналогового сиг- нала.

6. Восстановить аналоговый сигнал из дискретного путем выделения из спектра дис- кретного сигнала той части, которая соответствует спектру аналогового сигнала. Сравнить восстановленный сигнал с исходным аналоговым сигналом.

7. Повторить машинный эксперимент при в два раза меньшей частоте дискретизации. Убедиться в том, что восстановленный сигнал отличается от исходного аналогового сиг- нала, и объяснить причину искажения восстановленного сигнала.

Решение

Для моделирования аналогового сигнала преобразуем соотношение (1), определив количество расчетных точек i_s в периоде T₁ аналогового сигнала

T₁

i_s  _{ t}

 ¹ , F₁  t

С учетом последнего соотношения сигнал в расчетной точке i определяется следую- щим образом:

где



110 ³ 10 ^{3 }

x(i)  x₁(i)  x₂ (i)  x₃ (i),

3

(2)

1

x i  1cos^ 2 i

 0^  1cos1,953 10

 i,

_ 512 _

^ 2 10 ³ 10 ^{3  3}

x₂ i  0,5 cos^ 2 i



512

 0^  0,5 cos3,906 10



 i,



x₃ i  0 cos^ 2 i



3 10 ³ 10 ^3

512



 0^  0



xi  cos1,953 10 ^3  i 0,5 cos3,906 10 ^3  i

Количество расчетных точек в интервале дискретизации равно

i_d 

1

F_д   t

_ 512

8 10³ 10 ^3

 64

Поэтому вместо функции приведен на рисунке 2.

ut

можно рассматривать функцию

u i, график которой

u(i) 1

0 ⁱ

Рисунок 2

Сигнал

u i

формируется в цикле по порядковому номеру расчетной точки i с ис-

пользованием счетчика расчетных точек, переменная которого z изменяется от нуля до i_d.

Алгоритм формирования i – го значения сигнала u i приведен на рисунке 3

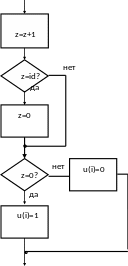
Рисунок 3 – Алгоритм формирования вспомогательного сигнала

Дискретный сигнал определяется следующим соотношением

x _Д i  xi ui.

(3)

Рассчитаем частоты спектральных составляющих дискретного сигнала, учитывая, что размножение спектра осуществляется по закону:

kF_d  F ,

где F – частота спектральной составляющей аналогового сигнала, k = 0, 1, 2, 3. . .

В рассматриваемом случае частота F принимает значения F₁, F₂ и F₃.

Расчет нужно выполнить при k = 0 и k = 1, а рассчитанные частоты представить в по- рядке возрастания.

Расчет частот спектральных составляющих дискретного сигнала по формуле

kF_d  F

k = 0

F=F₁, f₁ = F₁ = 1 кГц, F=F₂, f₂ = F₂ = 2 кГц, F=F₃, f₃ = F₃ = 3 кГц. K=1

F=F₃, f₄ = F_d – F₃ = 8 – 3 = 5 кГц, F=F₂, f₅ = F_d – F₂ = 8 – 2 = 6 кГц, F=F₁, f₆ = F_d – F₁ = 8 – 1 = 7 кГц, F=F₁, f₇ = F_d + F₁ = 8 + 1 = 9 кГц, F=F₂, f₈ = F_d + F₂ = 8 + 2 = 10 кГц, F=F₃, f₉ = F_d + F₃ = 8 + 3 = 11 кГц.

Построение спектральных диаграмм аналогового и дискретного сигналов

0 1 2 3 4 5 6 7 8 9 10 11 12 f кГц

Рисунок 4 – Амплитудный спектр аналогового сигнала

X/X_max

1

0,5

0 1 2 3 4 5 6 7 8 9 10 11 12 f кГц

Рисунок 5 – Амплитудный спектр дискретного сигнала

На рисунке 5 амплитудный спектр представлен в относительном масштабе по оси ор- динат как отношение амплитуды спектральной составляющей X к максимальной ампли- туде X_max.

1. Результат моделирования по программе «Diskret» при исходных данных таблицы 1 в виде временных и спектральных диаграмм аналогового и дискретного сигнала приве- дён на рисунке 6

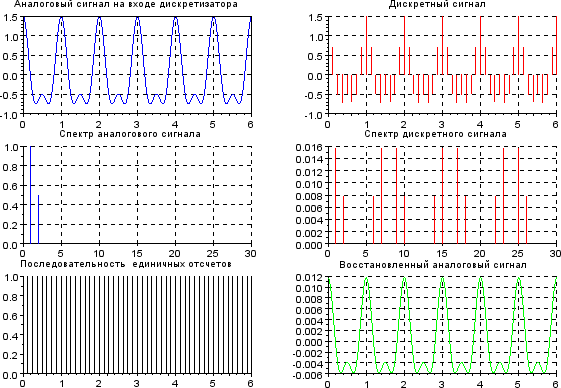
Рисунок 6. Временные и спектральные диаграммы при F_Д > 2F₃

Проанализируем полученные временные и спектральные диаграммы:

• Сравнивая спектры аналогового и дискретного сигналов, можно сделать вывод о том, что спектр дискретного сигнала представляет собой сумму бесконечно боль- шого числа «копий» спектра аналогового сигнала, расположенных на оси частот через одинаковые интервалы.

Иначе говоря: спектр дискретного сигнала состоит из суммы спектров исходного не- прерывного сигнала, сдвинутых друг относительно друга по оси частот на величину рав- ную частоте дискретизации F_Д.

Спектры аналогового и дискретного сигналов совпадают в диапазоне частот [-0,5 F_Д ; 0,5 F_Д]

Аналоговый сигнал, восстановленный из дискретного идентичен по форме исходно- му аналоговому сигналу, действующему на входе дискретизатора, но меньше по амплиту- де.

Выводы:

• Сгустки спектра дискретного сигнала соответствуют спектру соответствующего аналогового сигнала.

• Восстановленный сигнал полностью идентичен по форме исходному аналоговому и меньше по амплитуде.

• Несоответствие восстановленного сигнала исходному аналоговому сигналу по ам- плитуде обусловлено.

Повторим эксперимент при в два раза меньшей частоте дискретизации. Результат мо- делирования в виде временных и спектральных диаграмм аналогового и дискретного сигнала приведён на рисунке 7.

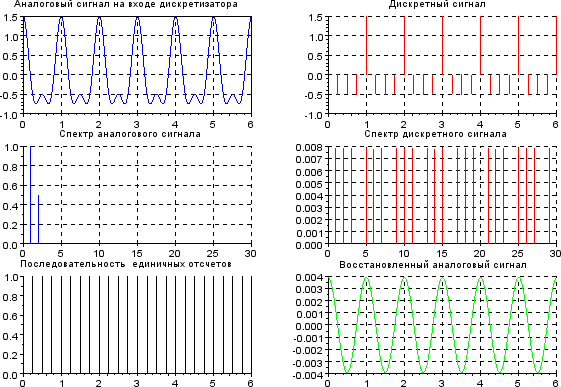
Рисунок 7. Временные и спектральные диаграммы при F_Д < 2F₃

Выводы:

• если условие F_Д > 2F₃ не выполняется (Рис 7), смежные спектры частично перекры- ваются. В этом случае сгустки спектра распределяются по оси частот неравномер- но, в результате чего возникает наложение спектров, приводящее к искажению

сигнала. Эти искажения являются неустранимыми и называются ошибками нало- жения.

• Сигнал восстанавливается без искажений, если выполняется условие (F_Д > 2F₃), в противном случае сигнал восстанавливается с искажениями, обусловленными ошибками наложения, что и доказывается при сравнении исходного аналогового сигнала и восстановленного аналогового сигнала.

Заключение:

При дискретизации аналогового сигнала возникают два эффекта, касающиеся спек- тра сигнала:

1. Эффект размножения спектра аналогового сигнала,

2. Эффект наложения сгустков спектра дискретного сигнала друг на друга.

Эффект наложения спектров приводит к искажению дискретного сигнала и невоз- можности точного восстановления аналогового сигнала из дискретного.

Спектр дискретного сигнала представляет собой периодическую функцию частоты, период которой равен частоте дискретизации.

Если дискретизации подвергается периодический аналоговый сигнал с линейчатым спектром, то размножение спектра осуществляется по закону:

kFд  F при k=0,1,..K

где F – частота спектральной составляющей аналогового сигнала.

Амплитуды спектральных составляющих дискретного сигнала пропорциональны со- ответствующим составляющим спектра аналогового сигнала.

Размножение спектра апериодического аналогового сигнала осуществляется по это- му же закону, если рассматривать в качестве F характерные частоты непрерывного спек- тра аналогового сигнала.

Эффект наложения спектров при дискретизации отсутствует, если выполняется условие Fд >2Fmax.

Задание №2.

Определение системной функции, комплексного коэффициента передачи, АЧХ и ФЧХ цифрового фильтра

Требуется определить системную функцию H(z), комплексный коэффициент передачи K(jθ), АЧХ K(f_N) и ФЧХ φ(f_N) цифрового фильтра, где θ = 2π f_N, f_N=f/F_Д – нормированная частота.

Построить графики АЧХ и ФЧХ

В таблице 2 приведены номер рисунка с графическим изображением алгоритма функ- ционирования цифрового фильтра и коэффициенты системной функции фильтра.

Номер варианта – последняя цифра номера студенческого билета.

Таблица 2. Алгоритм функционирования и параметры цифрового фильтра

Номер варианта	Номер рисунка	Коэффициенты системной функции фильтра
4	12	A11 = - A12 = - 0.2, A21 = A22 = 0.9

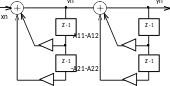
Решение:

Рисунок 8 (рисунок 12 МУ) Графическое представление алгоритма функциони-

рования фильтра

Определим системную функцию H(z), комплексный коэффициент передачи K(jθ), АЧХ K(f_N) и ФЧХ φ(f_N) цифрового фильтра, где θ = 2π f_N, f_N=f/F_Д - нормированная ча- стота.

Из рисунка видно, что

v_n   А1₁ v_n1  А2₁ v_n2  x_n y_n   А1₂ y_n1  А2₂ y_n2  v_n

2. Воспользовавшись свойствами Z-преобразования, перейдем от разностных уравне-

ний к уравнениям для Z-преобразований дискретных сигналов v_n, x_n, y_n

1

1

V (z)  X (z)  А1 z ^1V (z)  А2 z ^2V (z)

2 2

Выразим V(z) через X(z)

Y (z)  V (z)  А1 z ^1Y (z)  А2 z ^2Y (z)

1

1

X (z)  V (z)  А1 z ^1V (z)  А2

z ^2V (z)  V (z) 

X (z)

1

1

(1  А1 z ^1  А2

_z 2 ₎

Подставляя V(z) во второе уравнение, получим:

Y (z) 

1

1

(1  А1 z ^1  А2

X (z)

2

z ^2 )(1  А1

2

z ^1  А2

_z 2 ₎

Разделив Y(z) на X(z), получим системную функцию цифрового фильтра:

Н (z)  ^{Y (z)}

X (z)

1

1

2



^ (1  А1 z ^1  А2

1

2

z ^2 )(1  А1

1

z ^1  А2

_z 2 ₎ ^

1  ( А1  А1 )z ^1  ( А2  А1 А1  А2 )z ^2  ( А2 А1  А1 А2 )z ^3  А2 А2

_z 4

1 2 1 1 2 2 1 2 1 2 1 2

Определим комплексный коэффициент передачи, используя подстановку ^{z  e}j

K^ ( j ) 

1  ( А1

 А1

)e^{ j}  ( А2

 А1 А1

 А2

1

)e^{ j2}  ( А2 А1

 А1 А2

)e^{ j3}  А2 А2

_e j 4 ^

1 2 1 1 2 2

_ 1

1 2 1 2 1 2



1  ( А1₁  А1₂ )((cos( )  j sin( ))  ( А2₁  А1₁ А1₂  А2₂ )((cos(2 )  j sin( 2 )) 

 ( А2₁ А1₂  А1₁ А2₂ )((cos(3 )  j sin( 3 ))  А2₁ А2₂ ((cos(4 )  j sin( 4 ))

_ 1

1  1,76((cos(2 )  j sin( 2 ))  0,81((cos(4 )  j sin( 4 ))

Найдем АЧХ линии задержки:

K ( ) 





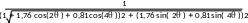
K ( j )  



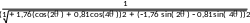
или

K ( f _N ) 

K ( j2f _N ) 

Построим график АЧХ (рисунок 9) при изменении f_N от 0 до 0.5 с шагом 0.0001. При-

нятый интервал изменения f_N соответствует интервалу частот от 0 до ^{FД 2} . Внутри этого

интервала (кроме частоты

^{FД 2} ) выполняется теорема Котельникова.

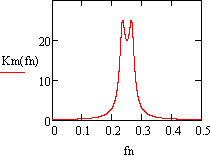Из графика АЧХ следует, что данный фильтр является полосовым. Его коэффициент передачи равен 20 при f_N =0.25, т.е. на частоте, равной 1/4 частоты дискретизации.

Рисунок 9 - АЧХ фильтра

Определим ФЧХ фильтра

Из выражения для комплексного коэффициента передачи следует, что его аргумент равен

   arg(K( j )).

^  (1,76 sin( 2 )  0,81sin( 4 )) ^

^ 1,76 sin( 2 )  0,81sin( 4 )

^ или

   arctg   arctg 

1  1,76 cos(2 )  0,81cos(4 ) 1  1,76 cos(2 )  0,81cos(4 )

   

^ 1,76 sin( 4 f _N )  0,81sin( 8 f _N ) ^

 f _N   arctg^

_ 1  1,76 cos(4

f _N )  0,81 cos(8



f _N ) _

График

 f _N 

приведен на рисунке 10.

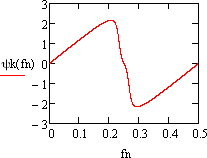
Рисунок 10 – ФЧХ фильтра

Для построения графиков АЧХ и ФЧХ воспользуемся программой, приведенной в Приложении Б. Имя программы: Расчет АЧХ и ФЧХ_4.

В строках 2-5 введем параметры A11-A22.

В строке 6 задается шаг изменения нормированной частоты delta_f, а в строке 4 диапа- зон изменения нормированной частоты от 0 до 0.5 с шагом delta_f. Затем в цикле по по- рядковому номеру расчетной точки m рассчитываются значения комплексной переменной z, системной функция H, АЧХ K(m) и ФЧХ phi(m). Строки 15-23 организуют вывод гра- фиков АЧХ и ФЧХ, которые приводятся на рисунке 11.

В среде Scilab основание натурального логарифма e записывается в виде %e, мнимая единица - %i, число π - % pi. Эти идентификаторы используются в строке 7 при записи выражения для z.

Чтобы воспользоваться данной программой при расчете других фильтров, заменим строку 11, а вместо строки 2 введем свои исходные данные.

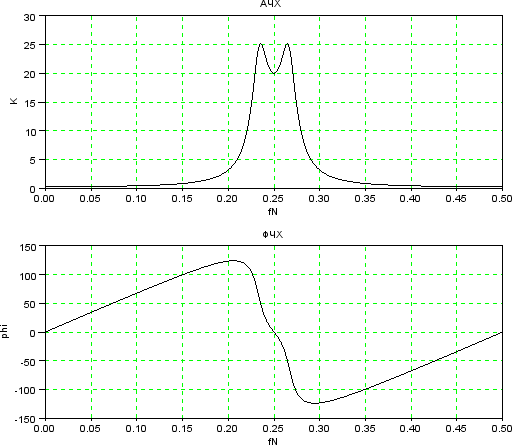
Рисунок 11 – АЧХ и ФЧХ фильтра

Задание №3.

Синтез нерекурсивного цифрового ФНЧ с линейной ФЧХ и гауссовской АЧХ методом ряда Фурье. Моделирование фильтра при действии на его входе полезного сигнала и по- мехи.

Требуется выполнить синтез цифрового фильтра с линейной ФЧХ и АЧХ, выражае- мой функцией Гаусса. Такие фильтры используются, например, при формировании сигна- лов гауссовской минимальной частотной манипуляции GMSK, применяемых в системе подвижной сотовой связи GSM.

Требуемая АЧХ фильтра выражается следующим соотношением

 _f ²

K f

  e

ln ^{ N }

 _fNg  _,

 

N

где f_N – нормированная частота – отношение абсолютного значения частоты f к часто- те дискретизации F_Д, σ – неравномерность АЧХ в полосе пропускания – отношение мак-

симального коэффициента передачи фильтра K_max к минимальному K_min в пределах поло- сы пропускания. Для гауссовской АЧХ

^Kmax

 K 0  1,

^Kmin

 K  f

 e^ln  ¹ .



Ng

На рисунке 12 показана гауссовская АЧХ в интервале нормированных частот от ну-

ля до 0.5 с использованием линейного масштаба по оси ординат при   2 и f_Ng = 0.05.

^{Пунктирная прямая, параллельная оси абсцисс, проведена на уровне} 1   0.707. ^{Абсцис-} са точки пересечения пунктирной прямой с АЧХ дает значение нормированной граничной частоты фильтра.

1

_KfN0.8

0.6

1

0.4



0.2

0

0

0.1 0.2 0.3 0.4 0.5

f_N

Рисунок 12 – АЧХ, описываемая функцией Гаусса

Параметры σ и f_Ng являются исходными данными для синтеза фильтра. Их значения приведены в таблице 3. Номер варианта – последняя цифра номера студенческого билета.

Реальная АЧХ отличается от идеальной пульсациями в полосе задерживания. Мак- симальный уровень пульсаций задаётся параметром δ_m, приведенным в таблице 3.

Требуется выполнить моделирование процесса фильтрации при действии на входе фильтра полезного сигнала и помехи.

Полезный сигнал представляет собой случайную последовательность элементарных посылок с уровнями 1 и -1. Количество отсчетов в элементарной посылке равно n0.

Амплитуда синусоидальной помехи Xp, нормированная частота помехи равна f_Np. Па- раметры n0, Xp и f_Np приведены в таблице 3.

Таблица 3. Параметры фильтра, сигнала и помехи

Номер варианта	fNg	σ	δm	n0	Xp	fNp
4	0.04	2	-50	25	1	0.30

Решение:

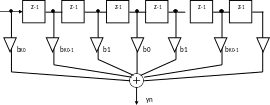
На рисунке 13 дано графическое представление алгоритма реализации нерекурсивно- го цифрового фильтра с линейной ФЧХ. Линейность ФЧХ обусловлена симметрией коэф- фициентов b относительно середины линии задержки. Длина линии задержки (количество элементов задержки) равна 2К0.

Синтез фильтра сводится к определению К0 и коэффициентов системной функции фильтра b.

^xn ^xn-1 ^xn-K0+1 ^xn-K0 ^xn-K0-1 ^xn-2K0+1 ^xn-2K0

^bK0

Рисунок 13 – Нерекурсивный цифровой фильтр с линейной ФЧХ

Из схемы рисунка 13 видно, что выходной сигнал фильтра y_n связан с входным сигна- лом x_n следующим соотношением

^yn ^{ b}0 ^xnK 0 ^{ b}1 ^xnK 01 ^{ x}nK 01 ^{ ..  b}K 01 ^xn1 ^{ x}n2K 01 ^{ b}K 0 ^xn ^{ x}n2K 0 ^.