Лабы / Лаба 2 / Malikov_0207_LR2

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ФЭТ

отчет

по лабораторной работе №2

по дисциплине «Электродинамика»

Тема: Микрополосковые линии передачи

Студенты гр. 0207 _________________ Маликов Б.И.

_________________ Горбунова А.Н.

_________________ Щубрет С.Л.

Преподаватель _________________ Ершов А.А.

Санкт-Петербург

2022

ЦЕЛЬ РАБОТЫ

Целью работы является исследование микрополосковой линии передач и резонаторов на их основе. Приобретение практических навыков использования векторного анализатора цепей.

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

Микрополосковая линия (МПЛ) (рис. 2.1, а) – это двухпроводная по- лосковая линия с поперечным сечением в виде параллельных прямых, име- ющая одну плоскость симметрии, параллельную направлению распростране- ния энергии (на рис. 1: 1 – проводящая полоска, 2 – экран (земляной электрод), 3 – подложка из диэлектрика).

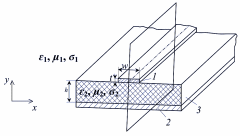
Рис. 1 - Микрополосковая линия (МПЛ)

МПЛ – в настоящее время наиболее широко применяемая СВЧ-линия передачи при разработке миниатюрных устройств СВЧ. Основным типом в МПЛ является квазиТЕМ-волна, однако могут быть возбуждены и волны высших типов. Структура поля в поперечном сечении МПЛ показана на рис. 2.

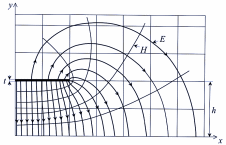
Рис. 2 - Структура поля в поперечном сечении МПЛ

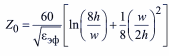Одной из важнейших характеристик МПЛ является волновое сопро- тивление, определяемое геометрическими размерами линии и диэлектриче- ской проницаемостью подложки. Для полосок нулевой толщины (t/h→0)

(1)

при соотношении w h < 1

(2)

где t – толщина микрополоска; h – толщина диэлектрика; w – ширина микрополоска; ε_эф – эффективная диэлектрическая проницаемость. В статическом случае _{εэф=(εr+1)/2+((εr -1)(1+10h/w)}^-1/2)/2. Следует отметить, что эффективная диэлектрическая проницаемость определяется распределением энергии распространяющейся электромагнитной волны между диэлектрической подложкой с относительной проницаемостью ε_r и воздушным пространством. Соответственно, значения ε_эф лежат в пределах от ε_r до 1.

Одним из простейших и в то же время важнейших элементов СВЧ-схем на основе МПЛ является микрополосковый резонатор (МПР), представляющий собой отрезок МПЛ резонансной длины l. На рис. 3 показан пример простейшего линейного разомкнутого на концах МПР.

Рис. 3 - Пример простейшего линейного разомкнутого на концах МПР

Основными характеристиками резонатора являются резонансная частота f₀ и добротность Q. Экспериментально эти характеристики могут быть получены на основе измерения характеристик передачи резонатора. Резонансная частота МПР определяется длиной резонатора l и диэлектрической проницаемостью подложки. Для линейного резонатора (рис. 3)

f₀ = 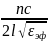(3)

где n = 1, 2, ... – число полуволн, укладывающихся на длине резонатора; ε_эф – эффективная диэлектрическая проницаемость микрополосковой линии на основе которой сделан резонатор.

Нагруженная добротность резонатора определяется как Q = f₀/∆f, где _∆f – ширина резонансной кривой.

СХЕМА ЛАБОРАТОРНОЙ УСТАНОВКИ

Исследуемый в данной работе векторный анализатор цепей «Обзор TR1300/1» (далее – «анализатор цепей») производства фирмы ООО «ПЛАНАР» предназначен для исследования передаточных характеристик радиочастотных цепей в частотном диапазоне от -60 до +10 дБм. Векторный анализатор цепей позволяет осуществлять измерение частотных зависимостей амплитуды, фазы, коэффициента стоячей волны, вещественной и мнимой части величины сопротивления, группового времени задержки для прошедшего и отраженного радиосигналов.

Характеристики МПЛ и МПР, измеряемые векторным анализатором цепей (ВАЦ), и схема измерений показаны на рис. 4.

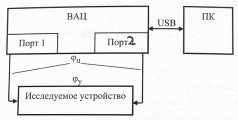
Рис. 4 - Схема измерений

Порт 1 ВАЦ является источником СВЧ-сигнала, который проходит через исследуемое устройство и затем поступает на порт 2 ВАЦ, являющийся приемником сигнала. Связь измерительного блока с персональным компьютером осуществляется через USB-интерфейс.

Во избежание влияния фазочастотных и амплитудно-частотных характеристик подводящих кабелей на снимаемые передаточные характеристики необходимо перед проведением измерений произвести калибровку.

РЕЗУЛЬТАТЫ ИЗМЕРЕНИЙ

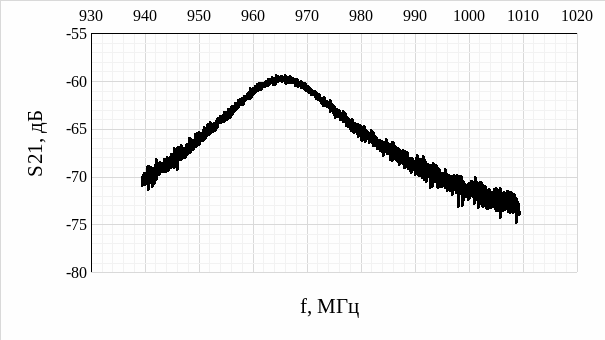
Рис. 5 – График зависимости коэффициента передачи «падающей» волны от частоты

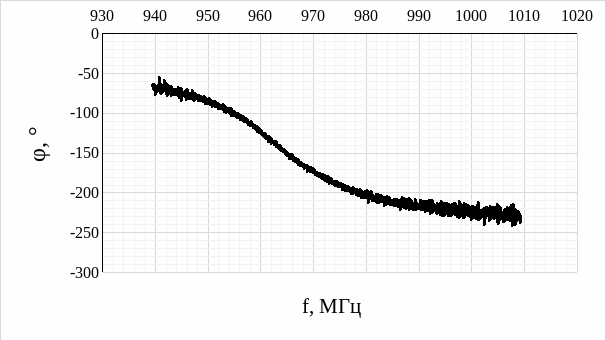
Рис. 6 – График фазочастотной характеристики МПР

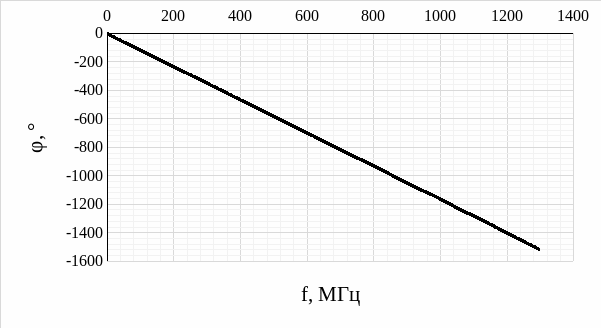
Рис. 7 – График фазочастотной характеристики МПЛ

Рис. 8 – График зависимости коэффициента отражения от частоты

ПАРАМЕТРЫ ИССЛЕДУЕМЫХ ОБЪЕКТОВ

Параметры МПР:

l = 80 [мм] = 0,08 [м] – длина резонатора

w = 3 [мм] = 0,003 [м] - ширина

h = 4 [мм] = 0,004 [м] – высота подложки

ε₁ = 4 – диэлектрическая проницаемость материала

Параметры МПЛ:

l = 360 [мм] = 0,36 [м] – длина полоски

w = 2,5 [мм] = 0,0025 [м] – ширина

h = 4 [мм] = 0,004 [м] – высота подложки

ε₁ = 9 – диэлектрическая проницаемость материала

ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

1. Вычисление резонансной частоты и добротности МПР:

По графику зависимости коэффициента передачи «падающей» волны от частоты (рис. 5):

f_0теор = 966 ·10⁶ Гц = 966 МГц – резонансная частота

f₁ = 957 ·10⁶ Гц = 957 МГц – нижний порог уровня 3 [дБ]

f₂ = 973 ·10⁶ Гц = 973 МГц – верхний порог уровня 3 [дБ]

По формуле добротности:

Q_теор = 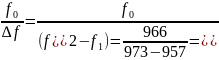60,375

Данные, полученные экспериментально:

f_0эксп = 965 ·10⁶ Гц = 965 МГц

Q_эксп = 60,912

Таким образом, сравнивая теоретические и экспериментальные значения, делаем вывод, что данные приблизительно совпадают, что говорит о точности теоретических вычислений.

2. Расчет эффективной диэлектрической проницаемости МПР и МПЛ:

2.1 Для МПР:

Общая формула нахождения эффективной диэлектрической проницаемости:

ε_эф =

Выводя из уравнения (3), с учетом f₀:

ε_эф =

Тогда, учитывая параметры МПР, приведенные ранее:

ε_эфтеор = 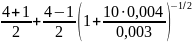= 2,896

ε_эфэксп = 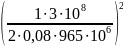= 3,775

Сравнивая полученные теоретические и экспериментальные значения эффективной диэлектрической проницаемости МПР, делаем вывод, что значения не совпадают. Данный факт может быть связан с неверным измерением параметров МПР, а именно, длины резонатора и ширины высоты подложки.

2.2 Для МПЛ:

ε_эф = 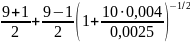= 5,970

3. Вычисление зависимости длины волны МПЛ от частоты:

3.1 Экспериментальная зависимость:

Длина волны:

λ_эксп =

Отсюда, волновое число:

k_эксп = =

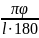
Примеры расчета при f = 1171 [МГц]:

Длина волны:

λ_эксп = 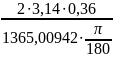= 0,094944 [м]

Волновое число:

k_эксп = = 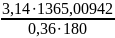= 66,17752 [рад/м]

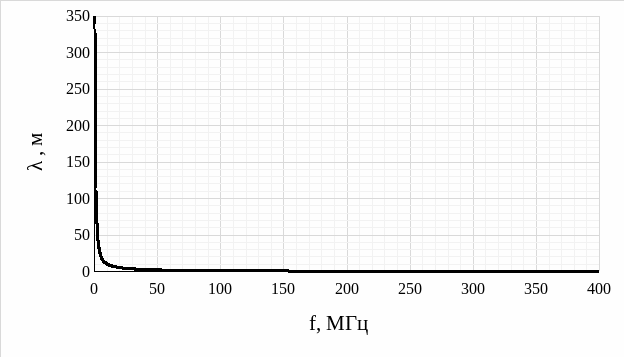
Рис. 9 – График экспериментальной зависимости длины волны от частоты

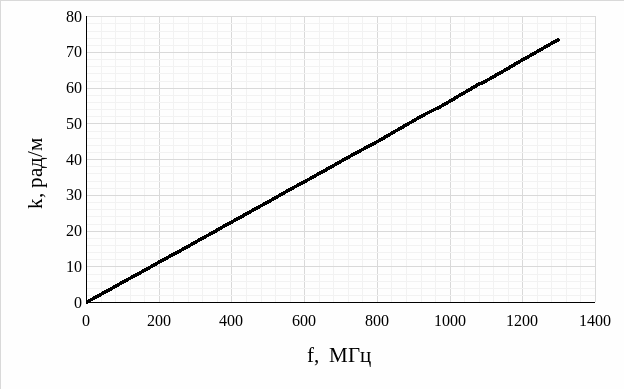
Рис. 10 – График экспериментальной зависимости волнового числа от частоты

3.2 Теоретическая зависимость:

Длина волны:

λ_теор =

Волновое число:

k_теор =

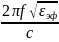
Примеры расчета при f = 1171 [МГц]:

Длина волны:

λ_теор = 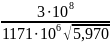= 0,104852 [м]

Волновое число:

k_теор = 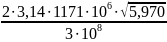= 59,92426

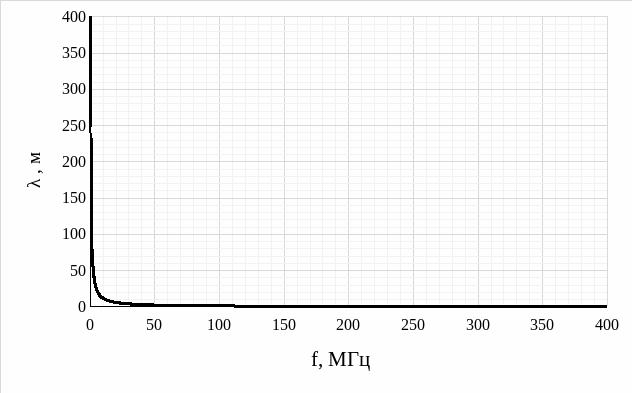
Рис. 11 – График теоретической зависимости длины волны от частоты (ε_эф = 5,970)

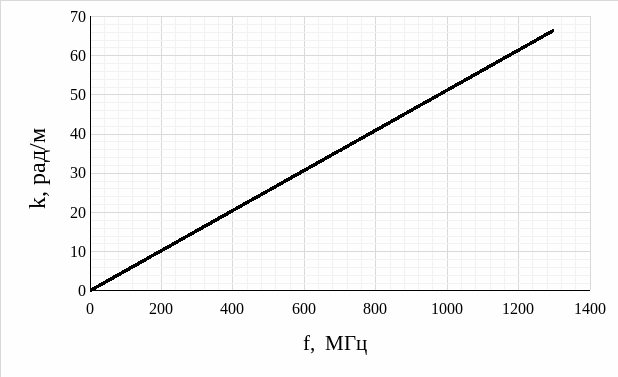
Рис. 12 – График теоретической зависимости волнового числа от частоты (ε_эф = 5,970)

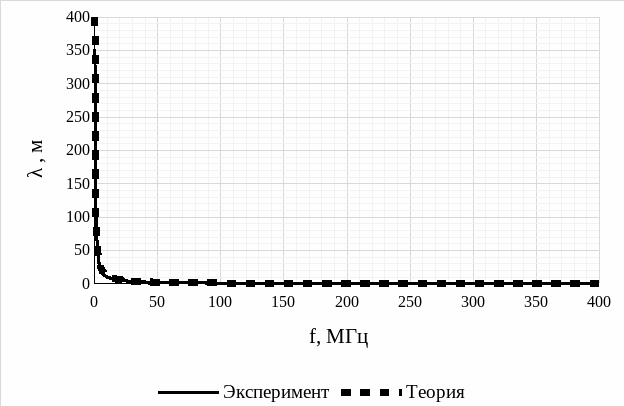
Рис. 13 – Сравнительный график экспериментальной и теоретической зависимостей длины волны от частоты

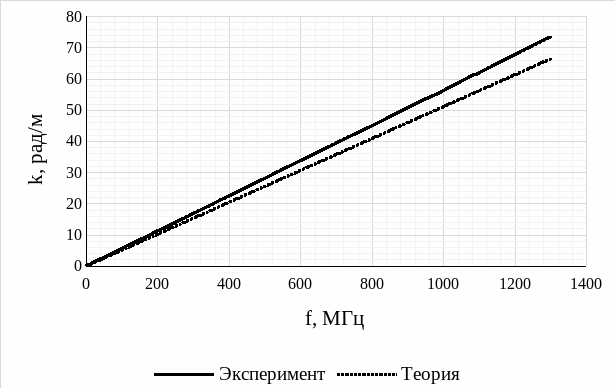
Рис. 13 – Сравнительный график экспериментальной и теоретической зависимостей волнового числа от частоты

ВЫВОД

Анализируя график экспериментальной зависимости длины волны от частоты (рис. 9), график теоретической зависимости длины волны от частоты (ε_эф = 5,970) (рис. 11), а также сравнительный график экспериментальной и теоретической зависимостей длины волны от частоты (рис. 13), делаем вывод, что график зависимости длины волны принимает гиперболический характер (то есть, с увеличением частоты длина волны уменьшается). Также, стоит заметить, что экспериментальные и теоретические значения практически совпадают.

Также, анализируя График зависимости коэффициента передачи «падающей» волны от частоты (рис. 5), вычислили значения резонансной частоты, а также значение добротности резонатора. При этом, сравнивая экспериментальные и теоретические значения, делаем вывод, что значения приблизительно совпадают, что говорит от высокой точности графического метода.

Проводя анализ графика экспериментальной зависимости волнового числа от частоты (ε_эф = 5,970) (рис. 10), графика теоретической зависимости волнового числа от частоты (ε_эф = 5,970) (рис. 10), а также сравнительного графика экспериментальной и теоретической зависимостей волнового числа от частоты (рис. 13), делаем вывод, что с увеличением частоты значение волнового числа линейно возрастает, то есть, возрастает число периодов волны, укладывающихся в отрезок 2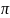 .