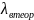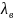МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра электронных приборов и устройств
отчет
по лабораторной работе №1
по дисциплине «Электродинамика»
Тема: Исследование дисперсии волн в волноводе и коаксиальной линии передач
Студенты гр. 0207 _________________ Маликов Б.И.
_________________ Горбунова А.Н.
_________________ Щубрет С.Л.
Преподаватель _________________ Зубко С.П.
Санкт-Петербург
2022
ЦЕЛЬ РАБОТЫ
Изучение свойств и конструкции коаксиальной линии и прямоугольного волновода, а также методики измерения длины волны в линии передачи и параметров, характеризующих режим ее работы. Ознакомление с законами распространения СВЧ сигналов в ограниченных средах (коаксиальной и волноводной регулярных линиях передачи). Получение практических навыков измерения СВЧ - сигналов.
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
Фазовая скорость (vф) и длина волны (λв) в линии передачи могут отличаться от соответствующих величин для свободного пространства (c; λв). Из анализа дисперсионных уравнений можно получить:

где λ0 – длина волны в свободном пространстве; εr, μr – относительные диэлектрическая и магнитная проницаемости среды; λкр – критическая длина волны в линии передачи; с – скорость света в вакууме.
Для линий с воздушным заполнением εr = μr =1 и

Наиболее распространенными типами линий передач в СВЧ-диапазоне
являются коаксиальная линия и прямоугольный волновод.
В коаксиальной линии (рис. 1, а) могут распространяться волны как дисперсионного, так и бездисперсионного типов. Волной бездисперсионного типа является ТЕМ-волна, для которой λкр=∞ и λв = λ0.
Структура поля ТЕМ волны показана на рис. 1, б. ТЕМ-волна является основной для коаксиальной линии.
Рис. 1 - Структура поля ТЕМ волны
В прямоугольном волноводе (рис. 2, а) могут распространяться только волны дисперсионного типа Hтр и Eтр. Для них

где a, b – поперечные размеры волновода. Наименьшую величину λкр имеет волна H10 (волн типов Eт0 и E0n не существует), называемая основной модой. Структура поля волны H10 показана на рис. 2, б.
Рис. 2 - Структура поля волны H10
Длину волны λкр и частотную дисперсию легко измерить, создавая стоячую волну. Для этого можно, например, расположить в поперечном сечении волновода проводящую стенку (короткое замыкание – КЗ) или образовать в каком-то сечении режим холостого хода (ХХ). Эпюры Е поля приведены на рис. 3: а – в режиме короткого замыкания и б – в режиме холостого хода. Для КЗ Г равен –1, для ХХ Г равен +1 (Г – коэффициент отражения).
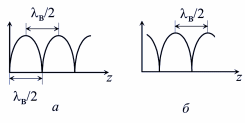
Рис. 3 - Эпюры Е поля
СХЕМА ЛАБОРАТОРНОЙ УСТАНОВКИ
Блок-схема лабораторной установки показана на рис. 4. Основным узлом установки является измерительная линия, представляющая собой отрезок соответствующей линии передачи, по которой скользит каретка зонда, связанная с измерительной линейкой. Индикатор позволяет определить положение максимумов и минимумов стоячей волны.

Рис. 4 - Блок-схема лабораторной установки
Коаксиальная измерительная линия (рис. 5) представляет собой цилиндрический проводник, расположенный между плоскопараллельными наружными пластинами. Такая линия является бездисперсионной, и структура полей в ней близка к структуре полей в коаксиальной линии.
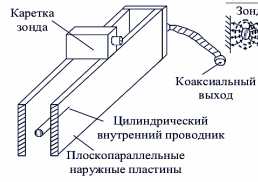

Рис. 5 - Коаксиальная измерительная
Волноводная измерительная линия (рис. 6) представляет собой отрезок прямоугольного волновода соответствующего сечения (дисперсия волн в прямоугольном волноводе требует применения различных измерительных линий в разных диапазонах частот).
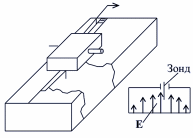
Рис. 6 - Волноводная измерительная линия
РЕЗУЛЬТАТЫ ИЗМЕРЕНИЙ
1. Прямоугольный волновод:
Табл. 1
При частоте f = 2,6 [ГГц]
U, мВ |
9,8 |
6,6 |
3,3 |
0 |
2,4 |
6,9 |
9,8 |
5,9 |
3,0 |
0 |
x, см |
1,0 |
2,6 |
3,9 |
5,9 |
7,5 |
9,1 |
11,0 |
12,7 |
13,6 |
15,4 |
Табл. 2
При частоте f = 3 [ГГц]
U, мВ |
10,0 |
6,4 |
1,6 |
0 |
4,6 |
8,0 |
10,0 |
6,8 |
2,9 |
0 |
x, см |
1,0 |
2,6 |
3,3 |
4,4 |
5,7 |
6,4 |
8,5 |
9,2 |
10,0 |
11,5 |
2. Коаксиальная линия передачи:
Табл. 3
При частоте f = 2,6 [ГГц]
U, мВ |
10,0 |
6,8 |
3,1 |
0 |
3,5 |
6,8 |
10,0 |
6,8 |
3,5 |
0 |
x, см |
3,6 |
4,2 |
4,7 |
5,5 |
6,4 |
6,9 |
9,3 |
10,0 |
10,3 |
11,5 |
Табл. 4
При частоте f = 3 [ГГц]
U, мВ |
10,0 |
6,8 |
2,3 |
0 |
3,0 |
7,4 |
10,1 |
6,5 |
3,1 |
0 |
x, см |
1,5 |
1,9 |
2,2 |
2,8 |
3,5 |
4,0 |
6,2 |
6,7 |
7,0 |
7,8 |
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
1. Построение графиков максимумов и минимумов стоячей волны:
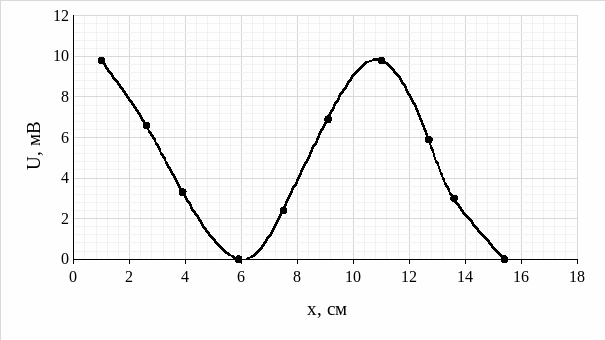
Рис. 7 – График максимумов и минимумов при частоте 2,6 ГГц в прямоугольном волноводе
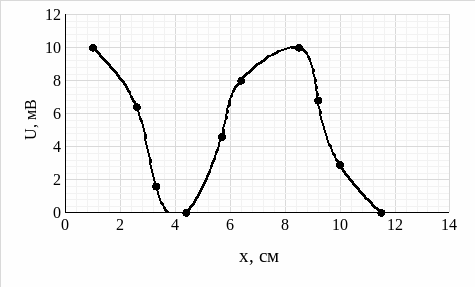
Рис. 8 - График максимумов и минимумов при частоте 3,0 ГГц в прямоугольном волноводе
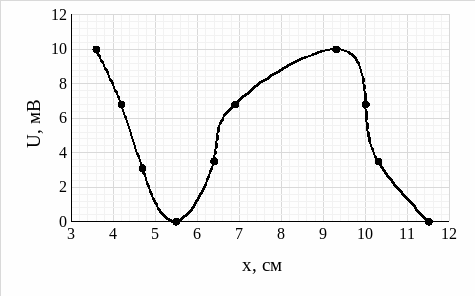
Рис. 9 - График максимумов и минимумов при частоте 2,6 ГГц в коаксиальной линии передачи
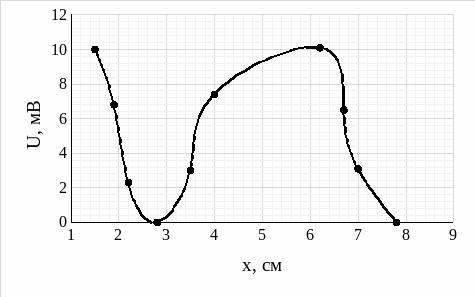
Рис. 10 - График максимумов и минимумов при частоте 3,0 ГГц в коаксиальной линии передачи

Рис. 11 - Сравнительный график максимумов и минимумов в прямоугольном волноводе при разных частотах
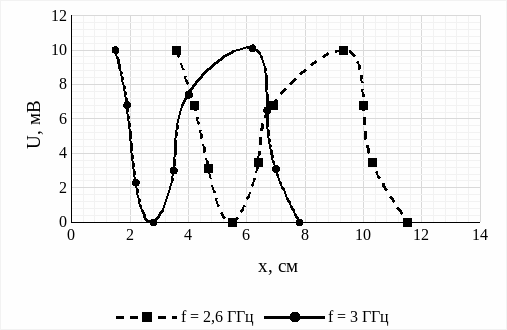
Рис. 12 - Сравнительный график максимумов и минимумов в коаксиальной линии передач при разных частотах
2. Вычисление длины волны:
2.1 Прямоугольный волновод:
Параметры волновода:
Ширина (a): 72 [мм]
Высота (b): 34 [мм]
2.1.1 Теоретический расчет:
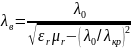

При m = 1, n = 0:
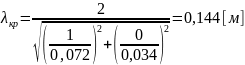
Пример вычислений для f = 2,6 ГГц:
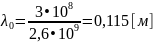
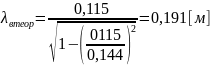
Пример вычислений для f = 3,0 ГГц:
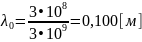

2.1.2 Экспериментальное вычисление:
По формуле:
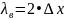
Пример вычислений для f = 2,6 ГГц:
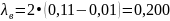 [м]
[м]
Пример вычислений для f = 3 ГГц:
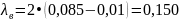 [м]
[м]
Табл. 5
f, ГГц |
|
|
2,6 |
0,191 |
0,200 |
3,0 |
0,139 |
0,150 |
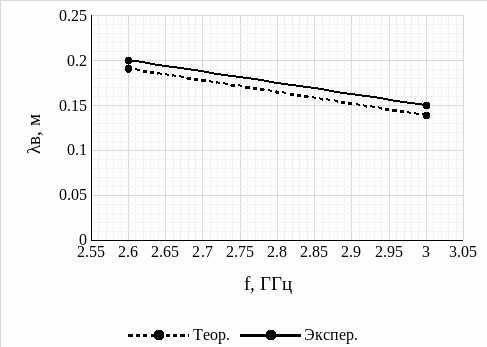
Рис. 13 – График зависимости длины волны от частоты прямоугольного волновода
2.2 Коаксиальная линия передач:
2.2.1 Теоретический расчет:
Пример вычислений для f = 2,6 ГГц:
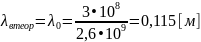
Пример вычислений для f = 3,0 ГГц:
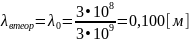
2.2.2 Экспериментальное вычисление:
По формуле:
Пример вычислений для f = 2,6 ГГц:
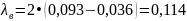 [м]
[м]
Пример вычислений для f = 3 ГГц:
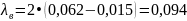 [м]
[м]
Табл. 5
f, ГГц |
|
|
2,6 |
0,115 |
0,114 |
3,0 |
0,100 |
0,094 |
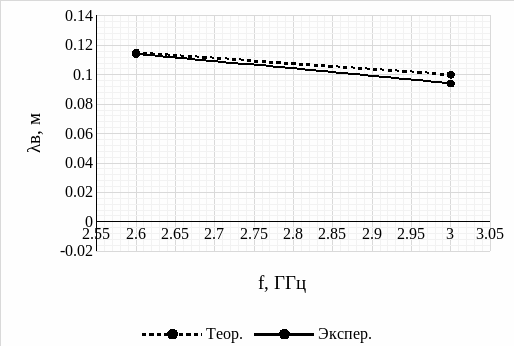
Рис. 14 – График зависимости длины волны от частоты коаксиальной линии передач
ВЫВОД
В ходе проведения данной лабораторной работы, были получены данные, а именно, значения напряжения максимумов и минимумов волны при изменении расстояния от ее начала. На основании полученных и обработанных экспериментальных данных, делаем следующие выводы:
Анализируя полученные графики рис. 11 и рис. 12 для прямоугольного волновода и коаксиальной линии передач, делаем вывод, что при увеличении частоты сигнала значения максимумов и минимумов волны смещается ближе к началу распространения волны. То есть, длина волны с увеличением частоты уменьшается.
Далее, анализируя графики рис. 13 и рис. 14 зависимости длины волны от частоты для прямоугольного волновода и коаксиальной линии передач, также можно сделать вывод, что с увеличением частоты длина волны уменьшается. Данный вывод подтверждается совпадением теоретических и экспериментальных расчетов.
При этом, стоит обратить внимание на тот факт, что было доказано распространение волны бездисперсионного типа (ТЕМ-волны) в коаксиальной линии передач, так как в результате вычислений было получено, что: λв = λ0 .