Методы / Луизов Цвет и свет

только определенных длин волн (λ1, λ2, .... λί, ..., λк), для которых энергия квантов (ε1,ε2,...,εί,..., εк) определяется формулой

εί = Еί – Е0

Так как εί = hνί = hс/λί, где h – постоянная Планка, а с – скорость света в вакууме, находим

Эта формула верна и для ионов, у которых уровнй энергии тоже дискретны. В твердом теле, где молекулы, атомы или ионы тесно сближены, они влияют друг на друга, изменяя допустнмые уровни энергии и, как правило, «размывая» их, т. е. уменьшая их дискретность. Поэтому пигменты поглощают кванты не со строго определенной длнной волны λί, а в некотором интервале длин волн от λ1 до λ2. Вместо линии поглощения они дают полосу логлощения. Некоторые пигменты обуславливают появление более чем одной полосы поглощения в спектре.

Положение и форма полос поглощения зависят от химического состава пигмента и от взаимного расположения атомов или ионов в кристалле. Не поглощенный в слое краски свет рассеивается, обуславливая характерный для данной краски коэффициент диффузного отражения, т. е. цвет краски при данном освещении.

9.2. Светофильтры.

. При производстве стекла, в особенности идущего на изготовление оптических приборов, следят за тем, чтобы в шихту не лопадали вредные примеси, т. е, вещества, уменьшающие прозрачность стекла. В особенности недопустимы такие примеси, которые поглощают свет селективно, так как они приводят к окрашиванию проходящего сквозь стекло света.

Сырьем для стекол с высоким коэффициентом пропускания не только в видимой, но и в ультрафиолетоврй области может служить оксид кремния SiО2, т. е. кварц. Расплавив чистый песок, можно получить прекрасное оптическое стекло, которое называют плавленым кварцем. Но, во–первых, очень чистый песок получить трудно. Обычно к нему примешаны в малых количествах оксиды различных металлов, прежде всего железа. Во–вторых, чистый кварц плавится при очень высокой температуре, около 1900 °С, что делает технологию плавки весьма сложной. Поэтому плавленый кварц весьма дорог и область его применения довольно узка.

Ряд веществ, не окрашивая стекла, значительно снижает температуру его варки. Например, стекло, имеющее состав 75 % SiO2, 15 % Na2О и 10 % СаО, варится при температуре 1450°С. Для обеспечения тех или иных требований, предъявляемых к стеклу, в зависимости от назначения, примешивают к нему и другие вещедтва; оксиды бария .(ВаО), динка (ZnО), магния (МnО), аллюминия (Аl2Оз), борный ангидрид {В2Оз). Для увеличения показателя преломления и дисперсии добавляют оксид свинца РbО (такие стекла называют флинтами).

Вещества, приводящие к избирательному поглощению и, следовательно, к окраске стекла, могут присутствовать в нем либо растворенном состоянии, либо в виде мельчайших коллоидных частиц. Окрашивание лри растворении дают оксиды или солн многих металлов: меди, никеля, железа, хрома, марганца, урана, вольфрама и др. Коллоидное окрашивание создают частицы золота, меди, селена и т. д. Так, например, один из видов зеленого стекла имеет состав: 72,5 % SiO2; 16 % Na2О; 5,5 % СаО; 3,5 % TiO2; .1,1 % СuО; 0,9 % А12О3; 0,5 %

Fе2О3.

Сведения о выпускаемых в Советском Союзе светофильтрах можно найти в стандарте ГОСТ 9411–81 «Стекло оптическое цветное». Обозначаются светофильтры двумя или тремя буквами и числом. Последняя буква (С) означает стекло, а стоящйе перед ней – начальные буквы цвета. Число – номер для различения ряда стекол, в разной степени пропускающих

примерно одну и ту же область спектра, Например, ССП – синее стекло № 11, СС15 – синее стекяо № 15, СЗСЗ – сине-зеленое стекло № 3.

Основная характеристика цветного стекла – коэффициент пропускания τ(λ) при длине волны λ Обычно он дается для светофильтра толщиной 2 или 5 мм (что специально оговаривается).

Существуют еще фильтры, ослабляющие одинаково, насколько это возможно, излучение всех длин волн видимого спектра. Их название – нейтральные стекла, обозначение

– НС1, НС2 и т; д. В упомянутом нами стандарте приводятся кривые пропускания одиннадцати стекол типа НС.

9.3. Спектральные приборы.

Получение от источника белого света направленного светового пучка определенного цвета стало воз-можным после изобретения простейшего спектрального прибора – призмы. Ньютон первый провел ряд целенаправленных опытов (о которых мы уже упоминали) по разложению солнечного света призмой (41), Он провел и первые опыты по смешению отдельных световых пучков, опыты, которые позволили ему дать общую схему законов сложения – круг Ньютона (см. рис. 5.1). Сейчас весьма узкие по спектральному составу световые пучки выделяются приборами, называемыми монохроматорами.

Основа монохроматора – призма, разлагающая проходящий сквозь нее свет в спектр вследствие того, что показатель преломления любого стекла зависит от длины волны света.

В монохроматоре источник света фокусируется на узкую щель, находящуюся в фокусе объектива. Выходящий из объектива параллельный пучок света падает на грань призмы, выходит из нее разложенным и попадает на второй объектив, который в своей фокальной плоскости дает изображение спектра. Поставив здесь вторую щель, можно выделить узкий пучок определенной длины волны, точнее, некоторый участок в спектре в интервале ∆λ. Поворачивая призму, можно получать на второй щели различные участки спектра, монохроматический свет той или ииой длины волны λ, (степень монохроматичности определяется величиной ∆λ).

Вследствие рассеяния света внутренними стенками монохроматора через вторую щель в небольшом количестве может проходить свет не только подлежащей выделению длины волны, но и других длин волн. Для повышения монохроматичности выделяемого света иногда применяют двойной монохроматор, в котором свет, выходящий из второй щели, проходит через систему, дублирующую первую систему монохроматизации.

Разложение света призмой количественно определяется угловой дисперсией 6, которая равна отношению изменения угла dφ, под которым луч выходит из призмы, к изменению

величиной ∆λ, обычно относимой к самой длине волны λ, т. е. отношением ∆λ/λ; обратную величину Вазывают разрешающей силой спектрального прибора

Здесь а – коэффициент пропорциональноети, который-веегда меньше единицы и может

кней приближаться.

Внекоторых монохроматорах прязма заменяется дифракдионной решеткой. Для решетки с числом штрихов N

где m – порядок спектра.

Призменные приборы могут выделять участки спектра с ∆λ, порядка десятых нанометра, а приборы с решеткой – порядка сотых я даже тысячных нанометра.

9.4. Спектральные линии.

Недостаток выделения узких участков спектра с помощью монохроматора заключается в том, что, поскольку участок вырезается из еплошного спектра, то чем меньше ∆λ, тем меньше интенсивность пучка. Пучки большой интенсивности и хорошей монохроматичности можно получать с помощью излучения раз-реженных газов, состоящего из ряда узких спектральных линий, длины волн которых характерны для каж-дого излучающего элемента.

Яркий желтый свет испускают пары натрия; дублет натрия состоит из .двух линий: λ = 589,0 нм и λ = 589,6 нм. Парй ртути дают много спектральных линий, из которых самые интенсивные: зеленая, λ = 546,1 нм; желтая, λ = 579,1 нм; фиолетовая, λ = 435,8 нм (приведены округленные значения длйн волн). На глаз цвет ртутной лампы воспринимается как зеленый, так как зеленая линия имеет наибольшую интенсивность и лежит близко к максимуму спектральной чувствительности глаза.

Монохроматическое излучение большой мощности могут давать лазеры. Из лазеров непрерывного действия наиболее известен гелий неоновый лазер. Он излучает свет с длиной волны λ = 632,8 нм мощностью от 1 до 50 мВт. Если взять некоторую среднюю мощность 10 мВт и принять во внимание, что для λ = 630 нм V(λ) = 0,265, мы получим световой поток Ф=1,5 лм. Чтобы оценить, много это или мало, предположим, что весь поток образует на белом экране с коэффициентрм диффузного отражения р = 0,9 светлое пятно диаметром 3 см (0,03 м). Яркость пятна окажется более 600 кд*м-2, т. е, весьма значительной.

Однако спектральное выделение излучений определенного цвета тоже имеет недостатки Так можио выделять только излучения некоторых длин волн, для которых в излучениях того или иного элемента имеются интенсивные спектральные лннни. Нет возможности плавно переходить от одной длины к соседней, что бывает необходимо при некоторых колориметрических измерениях.

Набор излучений, которые можно получить от лазеров, еще более ограничен, по крайней мере пока мы хотим применять общеупотребительные, хорошо отработанные лазеры. Таким образом, для некоторых колориметрических исследований монохроматор оказывается незаменимым.

9.5. Сложение цветов.

Проще всего сложить (т. е. смешать) цвета, выделенные светофильтрами или полученные от излучения спектральных линий, т. е. цвета направленных цветовых пучков. Достаточно направить подлежащие смешению пучки на белый экран так, чтобы они осветили одну и ту же площадку на экране. Тут мы и получим их смесь, результат их сложения.

Но и цвета окрашенных поверхностей – будем называть их накрасками – можно смешать. Пусть у нас имеются две карточки (1 и 2), окрашенные в цвета Ц1 и Ц2. Положим их на стол, а между ними поставим стеклянную пластинку. В данной схеме ее называют зеркалом Ламберта. Лучше, конечно, взять не просто стекло, а стеклянную пластинку, покрытую полупрозрачным металлическим слоем. Смотря сквозь зеркало на карточку 1, следует подыскать такое положение глаза, чтобы ее изображение на сетчатке совпало с изображением отраженной в зеркале карточки 2. Тогда наблюдатель воспримет некий суммарный цвет. Для точного расчета нужно, конечно, учесть коэффициент пропускания т и коэффициент отражения зеркала. р. Если приближенно считать, что они не зависят от длины волны, можно получить результат сложения:

Ц = τЦ1 + ρЦ2 (9.6)

Для смешения накрасок можно использовать также ограниченность пространственного или временного разрешения зрения. Если те же карточки с накрасками Ц1 и Ц2 разрезать на

полоскн шириной 2 мм, приклеить их на одии картон, чередуя цвета Ц1 и Ц2, а затем посмотреть на образовавшуюся решетку с расстояния четырех метров, мы не различим ее полос, а воспримем одноцветную площадку, цвет которой Ц будет равен сумме цветов Ц1 и Ц2. Здесь мы наблюдаем пространственное смешение цветов. Можно осуществить и временное смешение. Вырежем из карточек 1 и 2 два полукруга, укрепим на диске так, чтобы они образовали один круг, центр которого совпал бы с центром диска, и приведем диск во вращательное движение с угловой скоростью 50 Гц. Вследствие инерции зрения мы увидим суммарньш цвет Ц. С помощью вращающегося диска можно складывать и несколько цветов в разных пропорциях, которые определятся секторами, занимаемыми каждым цветом. По принципу такого сложения работает прибор, который носит название диска Максвелла. Диск Максвелла – одна из систем колориметра. Поэтому и расскажем мы о нем подробнее в следующей главе, посвященной колориметрам.

9.6. Координаты слагаемых цветов и симмарного цвета.

Если мы получаем свет с длиной волны λ, излучаемый в узком спектральном интервале ∆λ, цвет его Можно вычислить умножением спектральной плотности Pλ, принимаемой одинаковой в интервале ∆λ, на каждую из ординат сложения см. табл. 6.1 или 8.1) и на интервал ∆λ:

Если узкая полоса ∆λ выделена интерференционным фильтром из сплошного спектра со спектральной плотностью Pλ, то

r′ = Pλτ(λ)r (λ) λ; g′ = Pλτ(λ)g(λ) λ; b′ = Pλτ(λ)b (λ) λ .

Если фильтр выделяет из сплошного спектра широкую полосу излучений, для вычисления координат цвета приходится прибегать к интегрированию. Взяв за основу формулы (6.8), добавляем под интегралом множитель τ(λ) и получаем

Аналогичные формулы можно получить и для системы ХУZ на основе формул .(8.22);

Формулы (9.7) и (9.8) применимы и для вычисления координат цвета поверхности освещенного объекта. Следует только вместо τ(λ) поставить р(λ).

Если несколько пучков света направлены на одну площадку белого диффузного экрана, цвет освещенной площадки получим простым сложением коорди-лат смешиваемых пучков:

где ί – номер каждого из смешиваемых цветов; n – число смешиваемых цветов; r′ί, g′ί, b′ί –координаты каждого из цветов; г′, g′, b′ – координаты суммарного цвета, т. е. смеси.

Совершенно так же можно получить координаты смеси цветов в системе ХУZ, если нам известны координаты каждого цвета, полученные по формуле (8.22) или (9.8). А как найти координаты цвета, полученного при сложений цветов Ц1 и Ц2 с помощью зеркала Ламберта? Ответ дает формула (9.6). Если τ – коэффициент пропускания, а р – коэффициент отражения зеркала Ламберта, каждую координату цвета Ц1 нужно умножить на τ и сложить с соответствующей координатой цвета Ц2, умноженной на р. Значит для суммарного цвета

r′ = τr′1 + ρr′2; g′ = τg′1 + ρg′2; b′ = τb′1 + ρb′2

Рассмотрим случай, когда складываются цвета нескрльких накрасок, как при вращении диска Максвелла. Пусть сектор накраски с номером ί, цвет которой Цί, занимает на диске сектор, размер которого (в градусах) равен αί. Введем величину φί = аί/360°, которая

Практически решить задачу бывает значителъно сложнее, так как краски в какой-то степени влияют друг на друга. Человек научился пользоваться красками еще в доисторические времена. Рисунки первобытных людей на костях или на стенах пещеры нередко были окрашены. В качестве краски применяли растительные или минеральные вещества, например охру. Затем научились смешивать краски, постепенно в этом искусстве художники достигли большого совершенства, получая болыпое разнообразие цветов в своих картинах. Конечно, живописцы не пользовались никакими формулами. Но интуиция и опыт помогали им довольно быстро находить необходимый состав смеси и получать желаемый результат.

Нужно сказать, что опыт художников и размышления ученых о закономерностях в смешении красок наряду с наблюдениями смешения спектральных цветов помогли Ньютону и другим ученым заложить основы современной колориметрии.

Глава 10. Приборы для измерения цвета

10.1. Типы приборов.

Как мы уже говорили, после изучения свойств цвета и определения координат кривых сложения для стандартного колориметрического наблюдателя МКО 1931 г. цвет стал физическои величиной, которую можно измерять совершенно объективными методами, как массу или расстояние. Однако способы измерения цвета при непосредственном участии глаза тоже сохранились, применяются и, видимо, еще долго будут применяться. Потому приборы для измере-ния цвета – колориметры – нужно прежде всего разделить на визуальные и объективные. Представления о визуальном кодрриметре уже были даны в главе 6. Общее свойство всех визуальных колориметров то, что в них глазу предъявляются рядом два поля: поле изм«,ряемого цвета и поле сравнения. Варьируя цвет поля сравнения, добиваются его неотличимости от поля измеряемого цвета. Здесь глаз работает как нульприбор, устанавливающий равенство двух цветов с большой точностью. С какой именно – об этом будет рассказано в главе 17, посвященной порогам цветоразличения.

Основной недостаток всякого визуального колориметра состоит в том, что индивидуальные свойства цветового зрения человека, проводящего измерения, .отличаются от свойств зрения стандартного колориметрического наблюдателя МКО, что и вызывает характерную для данного оператора погрешность измерения. Погрешность будет тем больше, чем больше различие в спектральных составах уравниваемых цветов, и конечно, чем больше отклонение свойств зрения оператора. Бороться с таким недостатком визуального колориметра можно только отбором операторов. Конечно, к измерениям нельзя допускать явных цветоаномалов, но из людей с нормальным цветовым зрением можно выбрать тех, чье зрение ближе к зрению стандартного колориметрического наблюдателя.

Визуальный колориметр может быть аддитивным или субтрактивным. В аддитивном колориметре на поле сравнения направляется три (иногда и болыие) световых пучка, спектральный состав каждого из которых обуславливает один из трех основных цветов данного колориметра. Смедгаваясь в разных пропорциях, они дают возможность получить цвет, равный измеряемому цвету. Схема аддитивного колориметра изображена на рис. 6.1. Однако реально существующие (или существовавшие) аддитивные колориметры имеют мало общего с такой схемой.

Объективный колориметр можно строго согласовать с чувствительностью стандартного наблюдателя, с той точностью, которую допускают технические возможности прибора. Поля сравнения в объективном колориметре нет. Объективные колориметры в свою очередь подразделяются на колориметры без спектрального разложения исследуемого света и со спектральным разложением. В первом случае подлежащий исследованию световой пучок, например отраженный от цветового образца, разделяется на три пучка. Желательно, чтобы они имели равные интенсивности и одинаковый спектральный состав. Если такое условие нарушается, различия в пучках должны быть скомпенсированы или учтены при

градуировке прибора. Три пучка направляются на три фотоэлемента, чувствительность которых соответствует чувствительностям трех приемников стандартного колориметрического наблюдателя.

В колориметрах со спектральным разложением света пучок, цвет которого нужно измерить, направляется на призму или дифракционную решетку и затем мощность каждого узкого участка спектра измеряется фотоэлементом. Полученная таким образом спектральная плотность мощности Рλ пересчитывается в координаты цвета по формулам (8.22) или (8.27). Существуют и весьма широко применяются так называемые компараторы цвета. Их задача – устанавливать отличие в цвете того или иного товара или продукта от заданного образца цвета.

Наконец, для непосредственной визуальной оценки созданы атласы цвета. В них по определенной системе подобраны образцы накрасок, цвет каждой из которых известен. Оценка неизвестного цвета производится подбором близкого образца из атласа. При этом в атласе должно быть указано, при каком источнике света следует проводить сравнение.

10.2. Аддитивные колориметры.

Для построения аддитивного колориметра необходимо выбрать три основных цвета, смесь которых будет уравниваться с цветом изучаемого образца. Поэтому аддитивные колориметры чаще всего бывают трехцветными.

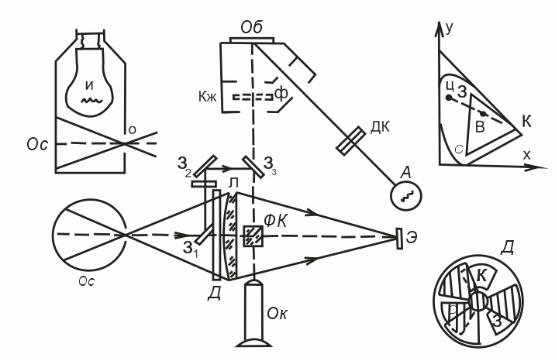
Рис. 10.1. Схема колориметра Л. И. Демкиной.

На рис 10.1 изображена схема трехцветного колориметра Л. И. Демкиной. Оператор, производящий измерение через окуляр Ок, видит поля фотометрического кубика ФК. Поля Л (см. рис. 3.2) освещены светом, идущим от исследуемого образца О6, а поля Э освещены светом от экрана Э. Экран освещается системой, состоящей из осветителя Ос, изображенного на схеме в разрезе горизонтальной плоскостью, и линзы Л. Разрез осветителя Ос вертикальной плоскостью изображен отдельно в верхней левой части рисунка. Мощная лампа накаливания И создает большую яркость белых внутренних стенок цилиндра, покрытых оксидом магния. Свет выходит из отверстия О, изображение которого линзой Л создается на белом матовом экране Э. Исследуемый образец прижимается к отверстию кожуха Кж, защищающего образец от постороннего света. Освещается образец лампой накаливания А с цветовой температурой 2854 К (источник А). Свет от лампы падает на

образец под углом 45°, а наблюдение ведется по нормали, что соответствует международно согласованным условиям цветовых измерений в случае светорассеиваюших образцов.

Цвет экрана Э, освещающего поля Э кубика ФК. (поле сравнения), можно изменять, пользуясь диафрагмой Д, которая отдельно изображена в нижней правой части рисунка. В металлическом круге вырезаны три отверстия в виде секторов, закрытых тремя фильтрами: красным К, зеленым 3 и синим С. Каждый фильтр в той или иной степени перекрывается заслонками (заштрихованные секторы), которые можно поворачивать независимо друг от друга. В зависимости от соотношения открытых площадей трех фильтров экран Э приобретает тот или иной цвет Ц. Изменение общей площади открытых частей светофильтров без изменения соотношения между ними изменяет яркость экрана Э, не меняя его цветности.

Измерение сводится к тому, чтобы, сдвигая заслонки на фильтрах, найти такое их положение, при котором поля кубика ФК не отличались бы друг ог друга. Если при равновесии оказалось, что открытая часть красного светофильтра равна к', зеленого з' н синего с', цвет образца можно считать измеренным:

Ц = к′К + з'З + с'С.

Принципиально цвет образца Ц измерен: к′, з′ и с′ – координаты цвета Ц. Однако измерен цвет только в системе КЗС, основные цвета которой зависят от конкретно примененных фильтров и спектральыого состава источника излучения И. Но определив основные цвета колориметра, т. е. найдя их координатьг в системе RGВ или ХУZ, уже сравнительно просто пересчитать координаты, к′, з′, с′ в координаты r′, g′, b′ или х′, у′, z′.

Алгоритм такого пересчета мы выведем несколько позже. А пока закончим рассмотрение рис. 10.1. Справа вверху на плоскост цветности ху изображена площадь реальных цветностей, ограниченная кривой спектрально-чистых цветов и прямой пурпурных, а также треугольник охвата реальных цветов системой КЗС колориметра. Образец может иметь цвет, след которого на плоскости цветности изображен точкой Ц. Цвет Ц лежит вне площади охвата, т. е. вне треугольника КЗС.

Мы видим, что цвет Ц лежит ближе к линии спектрально-чистых цветов, чем цвета внутри треугольника, т. е. чистота цвета Ц больше той, которую можно получить смешением стимулов КЗС в любом их соотношении. Уравнять поля кубика ФК. можно только, уменьшивчистоту цвета образца, как говорят, разбавив цвет, т. е. добавив на поле сравнения белого. Процесс разбавления цвета осуществляется с помощью зеркал 31, 32 и 33. Зеркало 33 – просто плоскопараллельная стеклянная пластинка, которая; отражает 10% свет и мало ослабляет свет, идущий от образца О6.

Разбавление можно производить и окрашенным светом. Для этого в пучок разбавляющего света вводится фильтр (обычно красный, такой же, как тот, что вставлен в диафрагму Д). Доля красного, вводимого в поле Л кубика ФК, должна вычитаться из доли красного, введенного в поле Э, и поэтому координата к' образца может оказаться отрицательной. В этом нет ничего удивительного, так как отрицательные координаты неизбежны в любой системе, основанной иа реальных цветах. Мы уже встречались с отрицательными координатами в системе RGВ.

Может оказаться, что яркость образца О6 слишком мала. Тогда для увеличения яркости образиа придвигают лампу А к кожуху Кж. Если, наоборот, яркость образца слишком велика, лампу отодвигают.

Как известно, цвет светорассеивающего образца зависит от спектрального состава освещающего его света. Мы сказали, что и в колориметре Демкиной используется источник А. Если цвет образца следует определить при источнике В или С (сведения об источниках света, принятых в колориметрии, будут даны в главе 13), спектральный состав источника А можно изменить включением жидкостных филыров.

Если нужно измерить цвет света, прошедшего сквозь светофильтр, на место образца О6 ставят белую рассеивающую пластинку, а внутрь кожуха вводят подлежащий измерению фильтр Ф.

Весь колориметр смонтирован в закрытую от внешнего света систему с выведенными наружу органами управления и отсчетными шкалами.

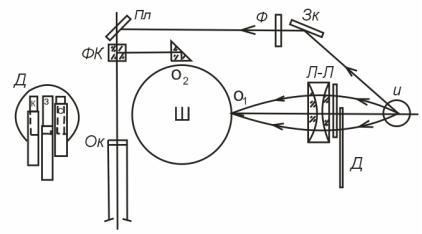
В трехцветном колориметре Дональдсона (рис. 10.2) свет от лампы И проходит сквозь фильтры, расположенные в диафрагме Д, и конденсором Л–Л направляется в фотометрический шар Ш через отверстие О1 В левой части рисунка изображена диафрагма Д с тремя прорезями, закрытыми фильтрами К 3 и С. Фильтры могут быть перекрыты заслонками, положение которых и создает смесь основных цветов колориметра в том или ином соотношении. Само смешение цветов происходит внутри шара, внутренняя поверхность которого покрыта оксидом магния. Из шара свет выходит через отверстие О2 и призмой направляется на поле сравнения фотометрического кубика ФК. Свет, отраженный от образца (не показанного на схеме), освещает другое поле кубика. Наблюдение ведется через окуляр Ок.

Рис. 10.2. Схема колориметра Дональдсона.

Разбавление измеряемого цвета может быть произведено с помощью зеркал Зк и Пл (пластинка) и фильтра Ф.

В колориметре Гилда диафрагма с фильтрами и заслонками. устроена примерно так, как в колориметре Демкиной, но смешение цветных пучков света совершается с помощью вращающейся призмы, которая направляет смешиваемые пучки на поле сравнения фотометрического кубика поочередно. Частота вращения призмы выше критической частоты слияния мельканий, и потому оператор воспринимает стационарную картину результата смешения основных цветов.

Принцип смешения во временн используется в уже известном нам диске Максвелла. Когда он применяется в качестве колориметра, в центре диска помещается кружок с накраской, цвет которой нужно измерить. Периферическая часть состоит из четырех секторов: красного, зеленого, синего и черного. Можно спросить, для чего понадобился черный диск. Дело в том, что три цветных сектора не могут быть независимы друг от друга, так как их суммарный угол равен 360°. Заданием двух секторов определяется третий. Следовательно, при трех секторах можно измерить только цветность, но не цвет. Черный сектор снимает однозначную взаимозависимость размеров цветньгх секторов, и теперь их размерами определяются координаты цвета. Раньше диск Максвелла часто применялся при контроле цвета товаров. Изредка применятся и теперь.

Примером аддитивного колориметра, в котором используется больше трех цветов, может служить шестицветный колориметр Дональдсона. В нем шесть фильтров: красный, оранжевый,: желто-зеленый, зеленый, сине-зеленый, синий. Применение шести фильтров вместо трех расширяет цветовой охват прибора.

10.3.Субтрактивные колориметры.

Всубтрактивном колориметре неразделенный пучок, освещающий поле сравнения, проходит последовательно все три фильтра. Каждый фильтр ослабляет какую-то часть спектра пучка, вычитает часть излучения, а оставшаяся часть определяет цвет поля сравнения.

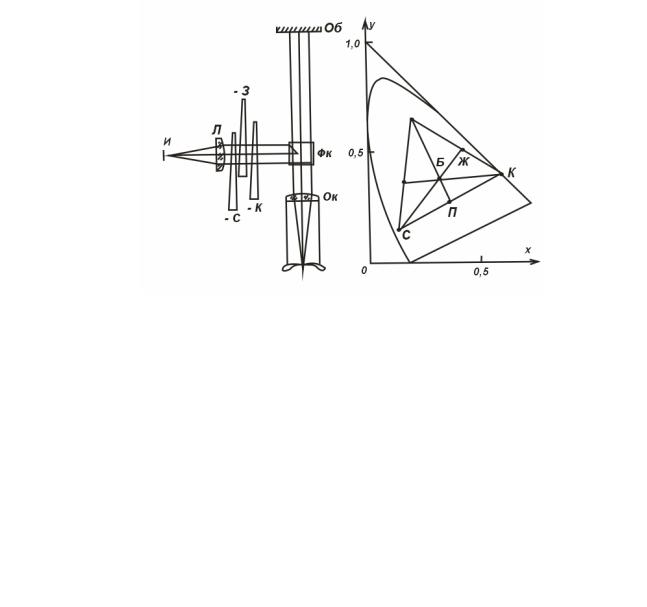
Схема субтрактивного колориметра изображена на рис. 10.3. Свет от источника И по пути к фотометрическому кубику ФК проходит через три фильтра (–С, –3 и –К,.т. е. минус синий, минус зеленый и минус красный), выполненные в виде клиньев. Другое поле кубика ФК. освещено светом, расреянным образцом О6. Наблюдение ведется через окуляр Ок. Обозначения клиньев символичееки указывают на ту часть спектра, которую они поглощают.

Разделим видимую часть спектра на три части: от λ = 380 нм до λ1, от λ1 до λ2 и от λ2 до

λ= 760 нм. Если положить λ = 500 нм, λ = 580 нм, можно условно назвать первую часть спектра синей, вторую – зеленой, третью – красной. Идеалом были бы такие три фильтра: – С поглощающий синюю часть спектра и полностью пропускающий зеленую и красную; цвет его желтый; – 3, поглощающий зеленую часть и полностью пропускающий синюю и красную; цвет его пурпурный; – К., поглощающий красную часть и полностью пропускающий синюю и зеленую; цвет его сине-зеленый.

Рис. 10.3. Схема субтрактивного колориметра.

Оператор, проводящий измерение цвета образца Об, перемещает клинья, вводя в пучок, освещающий поле сравнения, большую или меньшую толщину каждого из них, и наконец, добивается цветового равенства полей. Колориметр должеи быть отградуирован так, чтобы отсчеты положения клиньев сразу определяли цвет образца или по крайней мере давали возможность его рассчитать. В правой части рис. 10.3 схематически изображена область цветов {точнее, цветностей), которые можно измерить с помощью прибора.

Л. Н. Демкина и Г. С. Раутиан разработали полевой субстрактивный колориметр, т. е. прибор для измерения цвета предметов на местности. Схема его изображена на рис. 10.4. Основу его составляет зрительная труба, состоящая из объектива Л и окуляра Ок. В фокальной плоскости трубы поставлен фотометрический кубик ФК. Одно поле его освещено светом, рассеянным интересующим нас объектом Об, другое – светом, рассеиваемым белой пластинкой БП, которая освещена дневным светом, освещающим и изучаемый объект. Для регулировки общей яркостя лредусмотрен нейтральный клин Н. Следует указать, что цвет одного и того же объекта в разное время дня и в разные дни будет получаться различным, так как спектральный состав дневного света очень изменчив, о чем будет сказано в главе 12.