Методы / Луизов Цвет и свет

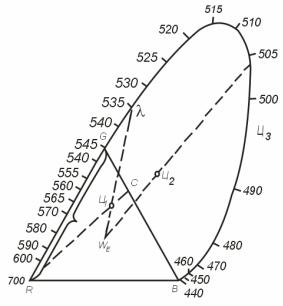
Чем отличаются два предмета, одинаковых по цветности, но разных по цвету? Один из них будет темнее другого. Единичному вектору соответствует единичный цвет, т. е. цвет, сумма координат которого равна единице. Любой цвет Ц может быть получен умножением единичного вектора на сумму координат цвета Ц, т. е. на его модуль. Если r, g и b – координаты цветности цвета Ц1 то яркость L(Ц1) его единичного вектора Ц1 согласно формуле (6.3) выражается так:

Как уже говорилось, цвет полностью определяется тремя координатами. Но ведь и для цветности даются три координаты r, g, b. Однако эти координаты не независимы. На них налагает связь формула (7.2). Две координаты уже однозначно определяют третью, которая не дает никакой новой информации. Именно поэтому цветность не дает полной информации о цаете. Обычно, характеризуя цветность, приводят только две ее координаты: r, g.

7.2. Цветовой треугольник.

Рассмотрим подробнее единичную плоскость, на которой изображается цветность (рис.7.1). Оси координат R, G и В пересекают плоскость единичных цветов в вершинах равностороннего треугольника. Точку, изображающую любую цветность, можно получить, найдя центр тяжести для грузов, привешенных к вершинам треугольника и пропорциональных координатам цветности r, g и b. Если r = g = b, грузы равны друг другу и центр тяжести оказывается на пересечении медиан трех углов треугольника, т. е. в его центре. Условие r = g = b определяет базисный стимул системы RGB и соответствует ахроматическому цвету WЕ – белому равноэнергетическому.

Рис. 7.1. Единичная плоскость в системе RGB

.

Чтобы найти центр тяжести для любой цветности с координатами r, g, b, приходится находить сначала точку центра тяжести на одной из сторон треугольника и помещать туда груз, равный сумме грузов на концах староны, а затем уже искать центр тяжести для суммы двух грузов и третьего груза. Обозначим сторону треугольника а, высоту его h, Для цвета Ц с координатами r′, g′ и b′ найдем сначала по формуле (7.1) координаты его цветности r, g, b. Теперь ойределйм расстояние s от вершины G до точкй C, на которую придется центр тяжести r и g:

Расстояние от вершийы R до точки С назовем l. Его нужно поделить на отрезок v (от точки R до центра тяжести Ц1) и отрезок l– v таким расчетом, чтобы соблюдалось равенство : r = (l – v)(g + b). (7.5)

Пользуясь теоремой Пифагора, найдем

Расстояние точки Ц1 от вершины G или В можно найти по формулам, аналогичным формулам (7.4) – (7.7). В формулы для расстояния до G не должна входить координата g, а для расстояния до В – координата b. Пользуясь формулами (7.4), (7.6) и (7.7), для любого цвета можно найти соответствующую ему точку на плоскости цветности.

Пусть дан цвет Ц1 для которого r′ = 1,35; g′ = 4,50; b′ = 2,00; координаты его цветности r = 0,172; g = 0,573; b = 0,255.

По формуле (7.4) находим s = 0,308a. Отложив s из вершины G на стороне GВ, получаем точку С, соединяем ее прямой с вершиной R и, найдя l и v по формулам (7.6) и (7.7), откладываем v = 0,735а на нрямой RС. Получаем точку цветности цвета Ц1

Для другого цвета Ц2 с координатами r′ = –1,10; g′ = 4,50; b′ = 2,50 координаты цветности будут

r = –0,187; g = 0,763; b = 0,424.

Из-за отрицательного значения r' и r сумма g+b>1, и поэтому v > l: точка Ц2 ложится вне треугольника.

Найдем теперь точки для спектрально-чистых цветов. Ординаты кривых сложения собраны в табл. 6.1. Деля каждую из ординат r (λ) , g(λ) и b (λ) на их сумму, получаем

координаты цветности r(λ), g(λ) и b(λ), которые тоже сведены в табл. 6.1. Нанеся эти точки на плоскость цветности, мы увидим, что точки, изображающие голубые и значительную часть зеленых цветов, ложатся далеко за пределами треугольника RGB, что соответствует отрицательному значению координаты r. Но от λ = 545 нм до длинноволнового конца спектра линия монохроматических излучений почти сливается со стороной треугольника RG. Правда, и здесь эта линия проходит вне треугольника, но близко к нему, что соответствует отрицательным, но малым по абсолютному значению b(λ)

7.3. Цветовой охват системы.

Цветности, лежащие внутри треугольника RGB представляют все цвета, которые могут быть получены смешеннем трех основных стимулов R, G и В, Этому треугольнику соответствует часть пространства, ограниченная плоскостями: r′ = 0 (след этой плоскости на плоскости цветности – сторона треугольника GВ); g′ = 0 (след – сторона RB) и b′ = 0 (след – сторона RG). Вне этого пространства существуют цвета, но у них по меньшей мере одна из координат должна быть отрицательной. Что же означает отрицательная координата? Пусть отрицательная координата r' (так чаще всего и бывает). Таков цвет Ц2 на рис. 7.1. Выходит, что для его получения нужно взять столько-то единиц цвета G, столько-то В и вычесть из смеси r' единиц красного цвета R. Но как можно вычесть из смеси зеленого и синего красный, которого там нет? Дёйствительно, реальным смешением трех стимулов системы RGB цвет Ц2 ,(как и всякий цвет, лежащий вне треугольника) получить нельзя. Площадь треугольника RGB определяет цветовой охват системы RGB.

Каждая система определяет цветовой охват, область тех цветов, которые могут быть получены смешением основных стимулов системы. Если бы вместо основного стимула G с длиной волны 546,1 нм взять стимул с длинйй волны 520 нм, цвет Ц2 попал бы в область, охваченную новой системой основных стимулов, его можно было бы получить их смешением, но вся система обладала бы новым цветовым охватом. Только совсем не

очевидно, что он был бы больше. В площадь нового треугольника вошли бы новые цвета, но многие другие из него бы вышли.

Что означают отрицательные координаты цвета при цветовых измерениях, мы уже знаем. Чтобы установить равенство цвета на полях сравнения колориметра, нередко одно основное излучение приходится добавлять к измеряемому цвету. Эта добавка и входит в координаты измеряемого цвета с отрицательным знаком.

7.4. Анализ плоскости цветночти.

Пусть на плоскости цветности имеется точка, изображающая какой–то цвет, например точка Ц1. Что можем мы сказать об этом цвете? Измерив сторону треугольника а и отрезки s, l и v, мы можем по формулам (7.4), (7.6), (7.7) найти координаты цветности цвета Ц1 Можно найти их и более простым способом. Опустим из точки Ц1 перпендикуляры на три стороны треугольника RGB и измерим эти перпендикуляры. Обозначим rh. – расстояние от Ц1 до стороны GB, gh – до стороны RB и bh, – до стороны RG. Измерение можно производить в любых единицах, скажем в миллиметрах. Затем измерим в тех же единицах высоту h треугольника RGB. Координаты цветности равны

Поскольку до сих пор мы оперировали стороной треугольника а, укажем, что, как легко видеть,

h = a 3/ 4 = 0,866a .

Конечно, найдя координаты цветности, мы еще не определили цвета Ц1. Координаты цветности обуславливают направление вектора цвета в выбранной системе координат (в данном случае RGB), но не определяют длины вектора, пропорциональной яркости цвета. И все же по плоскости цветности можно судить о некоторых свойствах изображаемых на ней цветов. Проведем прямую между точками Ц1, Ц2. Смешением этих двух цветов можно получить все цветности, изображаемые точками, лежащими на прямой Ц1Ц2.

Это правило относится, естественно, к любым двум точкам на плоскости цветности. Смешение основных стимулов R и В дает пурпурные цвета, которые не похожи ни на один из спектральных цветов. Пурпурным цветам дают название чаще всего по сходству их с известными цветками или плодами: сиреневый, малиновый. Если из точки любого спектрального цвета с длиной волны λ1 провести прямую через точку белого WE и продолжить прямую до линии спектральных цветов, длина волны λ2, соответствующая точке пересечения, будет дополнительной к длине волны λ1 по общему правилу, смешав излучения λ1 и λ2 в определенной пропорции, мы можем получить белый цвет.

Существует бесчисленное множество пар взаимно дополнительных излучений. Однако, если мы попробуем найти длину волны λ2, дополнительную к λ1 = 500 нм, проводя прямую через WЕ, мы пересечем прямую пурпурных цветов. Значит, одного спектрального излучения, дополнительного к λ1 = 500 нм, не существует. Нужно взять еще два излучения, смешанных в определенной пропорции. Область реально существующих цветов замкнута кривой спектрально-чистых излучений и прямой пурпурных цветов. Условно и пурпурные цвета причисляют к чистым излучениям и обозначают их тоже некоторой длиной волны λ′: зто длина волны излучения, дополнительного к чистому пурпурному.

Если мы возьмем на плоскости цветности любые три точки Ц1, Ц2 и Ц3, не лежащие на одной прямой, они определят некоторый треугольник, на площади его уместятся все цвета, которые можно получить смешением трех выбранных цветов. Эти три цвета, говоря теоретически, можно было бы принять за основные цвета некоторой системы, и соответствующий треугольник определил бы цветовой охват системы. А пользуясь и отрицательными координатами, можно было бы определять и все другие цвета.

7.5. Доминирующая длина волны λ и чистота цвета ρ.

Для того чтобы с помощыо плоскости цветности получить доминирующую длину волны λ любого изображенного на ней цвета Ц, достаточно через точку Ц, изображающую цвет, и точку WЕ провести прямую и продолжить ее до пересечения с линией спектральных цветов. Длина волны λ, соответствующая точке пересечения, и будет доминирующей длиной волны цвета Ц. Например, для цвета Ц1 λ = 535 нм (зеленый цвет).

Несколько сложнее определить чистоту цвета Ц. Вообще говоря, чем ближе точка Ц1. Вообще говоря, чем блтже точка Ц к линии спектральных цветов, тем больше чистота р цвета Ц. Но точный расчет усложняется тем, что яркость единицы белого цвета WЕ отличается от яркости единицы любого из спектральных цветов. (Следует помнить, что плоскость цветности не есть плоскость равной яркости.)

Будем характеризовать яркость единицы спектрально-чистого цвета с длиной волны λ величиной Lλ, а яркость единицы белого – величиной Lw. Абсолютные значения яркостей Lλ и Lw роли не играют: как мы сейчас увидим, в формулу войдет только их отношение.

Цвет Ц можно считать смесью m единиц белого и n единиц спектрально-чистого цвета с длиной волны λ. Чистота цвета р равна отношению яркости спектрально-чистого цвета в нем ко всей его яркости:

где LR, LG и LB – числа, пропорциональные яркостным коэффициентам.

Мы заменили тут координаты цвета координатами цветности ввиду того, что модуль цвета, равный сумме его координат, войдет и в числитель и в знаменатель дроби в (7.9) и сократится.

Соотношение между n и m найдем по правилу центра тяжести, считая, что груз n помещен в точку λ, а груз m – в точку We. Измерим расстояние q (от точки λ до Ц) и f (от

Для цвета Ц1 измерив f и q (в любых единицах, в любом, но одинаковом масштабе), найдем

нм, найдем r = –0,3304; g = 1.3105; b = 0,0199, откуда

Lλ = –0,3304 + 1,3105·4,5907 + 0,0199 0,0601 = 5,690;

LW = 13 5,651 =1,884 ,

Итак, для цвета Ц1 р = 0,488 ≈ 0,5.

При взгляде на рис. 7.1 кажется, что цвет Ц1 значительно менее чист, так как он гораздо ближе к белому, чем к спектрально-чистому. Это показывает только, что руководствоваться

просто соотношением расстояний до белого и спектрально-чистого для оценки чистоты нельзя.

Исследуем еще цвет Ц2, координаты цветности которого r = –0,186; g = 0,763; b = 0,423. Доминирующая длина волны для него (приблизительно) λ = 504 нм. Координаты цветности для этой длины волны с помощью табл. 6.1 находим методом интерполяции: λ = 504 нм; r = –

7.6. Нереальные цвета.

Рассмотрим теперь цвет Цз (см, рис. 7.1). Проведя линию из точки R до точки Ц3, увидим, что она делит сторону GB пополам, т. е. s = 0,5; отсюда по формуле (7.4) легко получить, что g = b. Вместе с тем, поделив формулу (7.7) на формулу (7.6), получим v/l = g + b. Измерив v и l на рис. 7.1 для цвета Ц3, найдем v/l = 2,04, т. е. g = b = 1,02, откуда r = – 1,04.

Определим теперь λ и р для цвета Ц3. Согласно рис. 7.1 λ = 494 нм. По табл. 6.1 и формуле (7.3) получаем Lλ = 3,562. Измеряя f и q, мы должны принять во внимание, что для Ц3 q – величина отрицательная. Поэтому

Чистота цвета Ц3 оказалась больше единицы, т. е. цвет Ц3 чище спектрально-чистого. Но это невозможно. Таких цветов в природе не существует. Цвета, лежащие вне пределов, очерченных линией спектральных и чисто пурпурных цветов, называются нереальньми цветами.

Поставив на плоскости цветности любую точку, мы можем найти ее координаты, доминирующую длину волны λ и чистоту цвета р. Но если точка лежит вне площади реальных цветов, для соответствующего ей цвета р>1, что и показывает его неосуществимость. Такой цвет не существует как физический стимул, но он однозначно определяется математическими параметрами: координатами, доминирующей длиной волны, чистотой. Более того, можно производить сложение или вычитание нереальных цветов, вычислять их яркость, как мы это только что сделали. Короче говоря, мы можем теоретически проводить с ними такие же операции, как и с цветами реальнымн. Скоро мы увидим, что введение в обиход нереальных цветов может принести существенную пользу колориметрии .

7.7. Изображение цветности в другой проекции.

Некоторые операции на плоскости r + g + b = 1 не очень удобны. Даже простое нанесение цветности в виде точки с помощью формул (7.4) – (7.7) – довольно сложная процедура. Поэтому плоскость цветности обычно проецируют на другую плоскость – перпендикулярную оси b. Такая проекция изображена на рис. 7.2. Видно, что большие отрицательные значения принимает только координата r, благодаря чему большая часть области реальных цветов лежит в левом верхнем квадранте. Отрицательные значения координаты g не достиают даже –0,02 и при малом масштабе рисунка едва заметны. Примерно такие же и отрицательные значения координаты b, которая на рисунке не изображена, но легко может быть найдена, так как b = 1 – (r + g). Правила определения доминирующей длины волны λ и чистоты цвета р остаются теми же, что и для плоскости r + g + b = 1. Если заданы две цветности (r1, g1) и (r2, g2), легко выяснить, какие цветности можно получать смешением цветов, соответствующих данным цветностям.

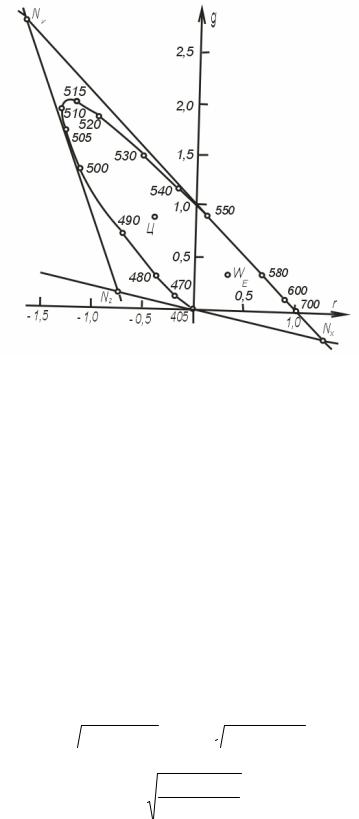
Рис. 7.2. Изображение цветности в координатах rg.

Достаточно провести прямую через точки (r1, g1) и (r2, g2), смешением можно получить все цветности на отрезке прямой между заданными точками. Преимущество графика на рис. 7.2 в том, что прямые здесь можно выражать аналитически. Чтобы прямая, уравнение которой

7.8. О Масштабе векторов цвета.

Познакомившись с единичной плоскостью и цветностью, мы можем точно определить масштаб, в котором измеряется модуль вектора цвета (в предыдущей главе мы ограничились наглядным примером).

Итак, снова будем обозначать l длину вектора цвета Ц, выраженную в тех же единицах, что и координаты цвета, а lц – единицу, которой нужно измерить l, чтобы получить модуль m цвета Ц. Отрезок lц зависит от направления вектора Ц и равен расстоянию от начала координат до точки, в которой вектор Ц пересекает единичную плоскость. Итак,

l = r'2 +g'2 +b'2 ; lЦ = r 2 + g 2 +b2 .

Модуль М цвета Ц получим как отношение l к lц:

Согласно формуле (7.1)

r’ = r(r’ + g’ + b’); g’ = g(r’ + g’ + b’) ; b’ = b(r’ + g’ + b’).

Подставив эти значения в числитель подкоренного выражения, после простых

сложении нескольких цветов: их яркости суммируются, что многократно подтверждено на опыте.

Таким образом, особенность метрики цветового пространства состоит в том, что единицы измерения модулей и яркостные коэффициенты зависят от направления векторов цвета.

Глава 8. Система XYZ.

8.1. Недостатки системы RGB.

Мы уже знаем, что невозможно выбрать такие три основных стимула, чтобы, смешивая их, подучить любой из существующих цветов. Смешение, как правило, уменьшает чистоту цвета. Правда, в длинноволновой области этот эффект слабо выражен: в диапазоне от 760 до 540 нм он практически отсутствует, Смешивая излучения 760 и 540 нм, можно получить все цвета, почти не отличимые от спектрально-чистых. Приложите линейку к вершине R цветового треуголышка на рис. 7.2 и проворачивайте линейку, чтобы она последовательно касалась точек 545, 540, 535 нм и т. д. Вы увидите; что начиная уже с 535 нм между линией спектралышх цветов и линейкой появится промежуток, который к 520 нм станет довольно широким. Чем он шире, тем меньше чистота цвета, который получится при смешении обуславливающего этот промежуток излучения со стимулом R.

Одного взгляда на рис. 7.1 достаточно, чтобы увидегь, что система RGB охватывает меньше половины площади, изображающей существующие цветности. Из рис. 7.2 видно, что почти 70% площади цветности лежит в области отрицательных значений координаты r. Это и есть существенный и главный недостаток системы RGB. Он довольно сильно усложняет различные колориметрические расчеты. У системы RGB есть несомненное достоинство – наглядность.

Немалое значение имеет также возможность непосредственного воспроизведения ее основных стимулов в колориметре. Но все же приходится констатировать, что системой RGB колориметристы теперь редко пользуются.

8.2. Возможность системы, охватывающей все цвета.

Невозможность построения системы из трех реальных стимулов, охватывающей все цвета, объясняется общей закономерностью: чистота цвета, как правило, снижается при смешении. Поэтому даже выбор трех спектрально-чистых стимулов не обеспечивает охвата многих (и даже болыпинства) цветов. Выход один: избрать в качестве основных стимулов цвета более чистые, чем спектральные, т. е. нереальные цвета. Выигрыш – возможность охвата всей области реальных цветов, выражение любого существующего цвета или цветности только положительными значениями координат. Потеря – невозможность реального воспроизведения основных стимулов, создания визуального колориметра на их основе,

8.3. Свобода выбора.

Переходя к нереальным цветам, мы получаем неограниченные возможности выбора основных стимулов. Ведь пока у нас только одно условие: треугольник, стороны которого соединяют точки, изображающие новые основные стимулы, должен включать в себя все существующие цветности. Значит, можно взять рис. 7.1 и поставить на нем любые три точки, удовлетворяющие поставленному условию. Таких комбйнаций трех точек может быть бесчисленное множество. Какие же точки выбрать? Такая свобода выбора может затруднить, но ее же можно разумно использовать, обеспечив определенные удобства создаваемой системы. Какие же требования предъявить к новой системе?

Прежде всего для сохранения преемственностй, а значит, и облегчения пересчета из системы RGB в новую систему следует оставить прежним базисный стимул: ахроматический

стймул в виде равноэнергетическогобелого WE. Стимул этот должен осуществляться при сложении трех новых основных стимулов и в равных количествах.

Следующее требование уже вносит нечто существенно новое. Большое неудобство системы RGB – существенное различие в яркостных коэффициентах ее основных стимулов. В новой системе можно было бы потребовать равенства яркостных коэффициентов. Однако создатели системы пошли по другому пути. Было решено, чтобы вся яркость цвета определялась одним стимулом, а яркость двух других была равна нулю.

Основные стимулы новой системы были названы X, Y и Z. В основу системы ХУZ

воспользуемся общей формулой для яркости цвета, т. е. формулой (7.3), положив в ней L(Ц) = 0. Так. как коэффициент К не равен нулю, нулю должен быть равен трехчлен,

Ясно, что для того чтобы удовлетворить условию (8.1), в системе ХУZ оси х, и z нужно провести в плоскости (8.2), а ось у перпендикулярно к ней. Но и это условие можно удовлетворить многими способами, так что свобода выбора еще остается. След плоскости нулевой яркости на рис. 7,2 будет прямой NzNx.

Чтобы найти ее уравнение, прежде всего учтем, что для плоскости цветности координаты цвета следует заменить координатами цветности, т. е. вместо r′, g′, b′ поставить r, g, b. Затем исключим из формулы координату b, воспользовавшись формулой (7.2),

Эта прямая, нанесенная на рис 7.2, называется «алихна», что в переводе с греческого означает «бессветная». Вторую сторону треугольника новой системы отложим на прямой, проходящей через точку (r1 = 1; g1 = 0) по касательной к длинноволновому концу линии спектрально–чистых тонов, чему удовлетворит выбор второй точки (r2 = 0,9797; g2 = 0,0205), через которую пройдет прямая. Согласно формулам (7.13) и (7.14)

От третьей прямой, ограничивающей новый цветовой треугольник, требуется только, чтобы она не пересекала поля реальных цветов и проходила не очень далеко от него. В

Точки пересечения Nх, Nу, Nz трех прямых (8.5), (8.6) и (8.7) будут вершинами треугольника новой системы XYZ. Пересечение алихны (8.5) с прямой (8.6) даст точку Nx, с прямой (8.7) – точку Nz, а пересечение прямых (8.6) и (8.7) – точку Nу.

Точки Nх, Nу и Nz нанесены на плоскость rg на рис. 7.2. Видно, что новый треугольник охватывает всю область реальных цветов.

8.4. Единичные основные цвета системы XYZ.

Казалось бы, проще всего принять точки Nх, Ny и Nz за концы единичных векторов системы ХУZ, т. е. принять за единичные цвета Цx, Цy, и Цz, координаты которых

Однако для системыXYZ был избран тот же базисный стимул и то же условие, что и для системы RGB: одинаковые количества основных цветов при сложении должны давать белый равнознергетический цвет WЕ. Достаточно взглянуть на рис. 7.2, чтобы понять, что, если в точки Nx, Nу и Nz поместить равные грузы, центр тяжести отнюдь не совпадет с точкой WЕ. Он окажется в точке Ц – в области довольно чистого голубого цвета.

Единичные цвета X, Y и Z следует выбрать так, чтобы сумма их была равна сумме единичных цветрв R, G и В, т. е. чтоб выполнялось условие

Не изменяя цветности цветов Цx, Цy и Цz, мы должны так изменить их модули, чтобы удовлетворить условию (8.10). Этого можно достигнуть, умножив Цx на α, Цy на β, Цz на γ,

Решение дает α = 1,8546; β = 0,5155; γ = 0,6299, Умножив первое из равенств (8.9) на α, получим слева αЦх, т. е. X, а справа выражение основного цвета X через основные цвета R,G и B. Таким же образом второе уравнение даст Y, третье Z. В результате получены уравнения

Z = –0,4681R + 0,0888G + 1,0092В.

Сложив все три уравнения почленно, убедимся, что Х + Y + Z = R + G + В, т. е. что равенство (8.12) удовлетворено и, следовательно, сумма единичных (и любых равных количеств) цветов X, Y, Z дает белый равноэнергетический цвет.

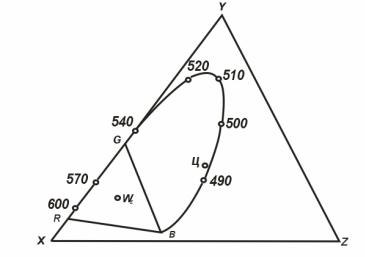
Рис. 8.1. Следы осей x, y и z на плоскости rg.

На рис. 8.1 плоскость чертежа совпадает с плоскостью (8.10). Видно, что точка Ц попала теперь в центр треугольника ХYZ и, следовательно, соответствует белому равноэнергетическому цвету в системе ХYZ, так же как точка WЕ в треугольнике RGB. (Мы не

поставили вместо Ц снова символ WЕ, чтобы избежать двух одинаковых обозначений на одном чертеже.)

8.5. Переход от системы XYZ к системе RGB и обратно.

Переход от одной системы цветовых координат к другой определяется общими правилами преобразования координат. Пусть у нас имеется некоторый цвет Ц, изображаемый вектором в пространстве. Будем считать, что в обеих системах, соотношение между которыми мы хотим установить, направление вектора остается неизменным. Соотношения между основными координатами двух систем определяются формулами

Коэффициенты при R, G и В – постоянные величины, характеризукнцие переход от системы RGВ к еистеме ХУZ. Смысл их совпадает с коэффициентамй формул (8.13), и, следрвательно, для интересующего нас частного случая двух систем все девять

Для получения формул обратного перехода следует, рассматривая уравнения (8.18) как

Таким образом, мы получили фррмулы для вычисления координат цвета х′, у′ и.z′ по координатам r′, g′ и b′ (формулы (8.19)) и для обратного перехода из системы ХYZ в систему

RGB (формулы (8.18)).

8.6. Согласование систем по яркости.

Формула (8.19) прмещена.в ГОСТ 1388–67, следовательно, узаконена. Но вслед за формулой помещено указание, рекомендующее умножить результат вычислений на некоторую постоянную величину а = 5,6504. Чем вызвано такое указание? В обеих системах принято, что смешение равных количеств основных стимулов дает белый равноэнергетический цвет WE. Будем считать, что WE мы получаем, смешивая три единичных стимула как в одной, так и в другой системе, Теперь сопоставим яркостные коэффициенты обеих систем. Обратимся к формулам (6.1) и (8.1)

LR: LG: LB = –1: 4,6907: 0,0601;

LX: LY: LZ = 0: 1: 0