Методы / Луизов Цвет и свет

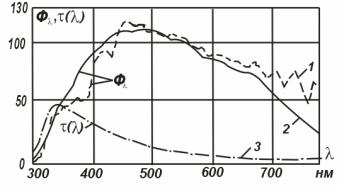
Рис. 13.2. Распределение спектральной плотности мощности в источнике D65 (кривая 1) и в образце Вершинского (кривая 2). Кривая 3 – спектральный коэффициент пропускания

фильтра в образце Вершинского.

По-видимому, создать модель, которая с достаточной точностью воспроизводила бы все зубцы стандартного излучения D65 (так же как и D55 или D75), возможно только с помощью спектрального разложения света первичного источника и введения спектральных масок. Но возникает вопрос: зачем? Зачем затрачивать такие усилия и создавать сложную и трудно воспроизводимую модель источника D65: чтобы соблюсти практически бесполезные требования к ней? Конечно, сложная форма каждой экспериментально полученной кривой распределения спектральной плотности мощности дневного света отражает, какие-то свойства атмосферы Солнца и атмосферы Земли. Эти свойства могут быть интересны геофизикам. Но для колориметрии практический интерес могут представлять только усредненные данные, а в них по меньшей мере странно отражать мелкие детали формы усредняемых кривых. В самом стандарте кривую D65 следовало бы сгладить. И дальше: ведь предлагаются и другие источники D, например D55, D75 или вообще D для любой коррелированной цветовой температуры. По нашему мнению, эти температуры не должны быть слишком высоки. Мы уже указывали на целесообразность принять ее близкой к 5200 К. И лучше всего было бы, сохранив главное преимущество источников типа D, – введение нормирования ультрафиолетового излучения – взять за основу коррелированную цветовую температуру Tц = 5200 К или даже просто излучейие черного тела при Т = 5200 К. Кривая спектральной плотности такого излучения не нуждается в сглаживании. Воспроизвести ее было бы, видимо, не слржнее чем кривую источников В или С. Потребовалась бы только лампа накаливания с кварцевой колбой и подбор цветных фильтров. Так мог бы быть осуществлен стандартный источник D52.

13.7. Современные источники света.

Применяющиеся сейчас источники света весьма разнообразны, и поэтому одна и та же накраска может в широких пределах менять свой цвет в зависимости от освещения.

С начала нашего века все шире распространялись электрические лампы накаливания, которые и сейчас еще, значительно усовершенствованные, господствуют в осветительной технике, поскольку наши жилища все еще в основном освещаются ими. Поэтому совершенно естественно введение стандартного источника А в виде вольфрамовой лампы накаливания. При освещении лампами накаливания цветность предметов близка к той, какую создает источник А. Но, конечно, цветность при источнике А сильно отличается от цветности при дневном свете.

Однако на поиски новых источников света толкала не плохая цветопередача, характерная для ламп накаливания. Практически важен был другой их недостаток: малая экономичность, малый коэффициент полезного действия (КПД). Мы знаем, что максимальная световая отдача Km = 683 лм·Вт–1 получается в том случае, когда вся мощность излучается на длине волны 555 нм. КПД источника света η есть отношение его световой отдачи K к Km:

Расчет показывает, что черное тело обладет максимальным КПД при температуре 6600 К (15). Вольфрам плавится при гораздо более низкой температуре (3680 К), и поэтому обычные лампы накаливания имеют температуру 2800–2900 К, чему соответствует КПД около 3%. Всякими хитростями, как напрймер в йодно-кварцевых лампах, удаётся повысить уемпературу почти до 3400 К, чему соответствует η = 6 %, и это предел для лампы накаливания.

Сейчас стали применять газоразрядные лампы с натриевым, ртутным и ксеноновым наполнением. Они дают линейчатый спектр, характерный для данного газа. Но при повышении давления линии расширяются и газоразрядные лампы начинают давать излучение со сплошным спектром с максимумами на местах бывших линий. Сейчас все шире входят в употребление ксеноновые лампы высокого и сверхвысокого давления. Но все же их КПД не превышает 6%.

Вее более широкое применение, постепенно вытесняя лампы накаливания, получают сейчас люминесцентные лампы. Общественные здания постепенно переходят на люминесцентное освещение, проникают они и в наши квартиры.

Люминесцентная лампа выполнена в виде трубки, в концы которой впаяны электроды. Разряд проио ходит в атмосфере аргона с примесью паров ртути. Ртуть излучает несколько спектральных линий в видимой и ультрафиолетовой областях. Внутренние стенки трубки покрыты тонким слоем люминофора – порошка, который, поглощая коротковолновое излучение, излучает сплошной спектр. Часть излучения спектральных линий все же пробивается через порошок непоглощенной, образуя местные максимумы на кривой спектральной плотности мощности. Подбором люминофора можно в широких пределах менять форму этой кривой, создавая имитацию той или иной цветовой температуры. Возможность избежать участия теплоты в процессе преобразования электрической энергии в световую позволяет сделать люминесцентные лампы эконодоичнее ламп накаливания, доводя их КПД до 9% (втрое больше, чем у обычных ламп накаливания).

Нужно заметить, что КПД осветительной лампы не только нельзя, но недопустимо стремить к 100%, Очень высокий КПД можно получить от газоразрядной натриевой лампы. Пары натрия излучают две близкие спектралыше линии: 589,0 и 589,6 нм, для которых V(λ) ≈ 0,75 .В экспериментальных образцах натриевой лампы удавалось получить КПД около 60%. Но желтый евет ее совершенно непригоден для обычного освещения, никакие цвета предметов при нем не различаются. Впрочем, натриевые лампы иногда применяют для освещения дорог.

Наиболее экономичным источником был бы такой, у которого относительная спектральная плотность мощности Фλ в видимой области была бы, как у черного тела при Т = 6600 К, а в ультрафиолетовой и в инфракрасной области Фλ равнялась бы нулю. Расчет показывает, что у такого идеального излучателя видимого света КПД был бы приблизительно 35%. Как видим, все известные нам источники света далеки от этого идеала. Ближе всего к нему Солнце, для которого η = 14%. Впрочем, нужно учесть, что в экономике природы весь солнечный свет полезен, а его ультрафиолетовую часть считают важной и колориметристы, стараясь воспроизвести ее в источнике В.

13.8. Типы люминесцентных ламп.

Первые люминесцентные лампы были названы лампами дневного света (ЛДС). Цветовую температуру их излучения положили равной 6500 К (как у источника D65).

Тут и обнаружилось странное явление психологического порядка: создаваемое ими освещение многим показалось неприятным, свет ощущали холодным. Видимо, с вечерними и ночными условиями, с более слабой освещенностью ассоциируется свет е преобладанием длинноволнового излучения – красноватый, тот, что создается лампами накаливания. Здееь уместно вспомнить, что в начале века после еще более красного света свечей и керосиновых

ламп многие чувствовали себя неуютно при свете ламп накаливания, а поэты называли его «голубым электрическим светом».

Чтобы пойти навстречу эмоциям, были созданы разновидности люминесцентных ламп: лампы холодного белого света (ЛХБ, ТЦ = 4300 К), белого света (Тц = 3500 К) и теплого белого света (ЛТБ, Тц = 2800 К, как у лампы накаливания).

Следует заметить, что, чем больше общая освещенность, тем более высокая Тц воспринимается как приятная или хотя бы допустимая: видимо, потому, что при высокой освещенности условия станск вятся похожими на дневные.

Глава 14. Коэффициенты отражения и пропускания.

14.1. Отражение и пропускание.

Зрение дает нам обильную информацию о внешнем мире только потому, что все окружающие нас предметы отражают или пропускают свет. Воздух, вода, стекло пропускают свет и позволяют ему достигать наших глаз или освещать другие предметы; Непрозрачные тела, отражая свет, позволяют нам видеть их. При этом чаще всего происходит диффузное отражение, иначе называемое рассеянием. Если бы отражение было зеркальным, мы видели бы не сам предмет, а источник света или другие предметы, рассеивающие свет. А если бы предметы вообще не отражали света, мы могли бы видеть только источники света: Солнце, Луну, звезды, лампы. Немного бы мы узнали о мире в таком случае.

Как отражение, так и пропускание бывает обычно селективным, т. е. неодинаковым для разных участков спектра. Отражение света от предметов при попадании в глаз отраженного ими света позволяех воспринимать размеры и форму предметов, а селективность отражения

– их цвет. Сейчас нам предстоит уточнить некоторые вопросы, связанные с селективным отражением и селективным поглощением или пропусканием света.

14.2. Коэффициент отражения.

Говоря об отражении, мы подразумеваем, что часть света, упавшего на поверхность раздела двух сред, возвращается обратно в ту среду, из которой пришел свет. Отношение мощности, возвращающейся в первоначальную среду, ко всей мощности падающего на ловерхность света мы назвали коэффициентом отражения ρ. Эту величину для монохроматического света с длиной волны λ мы обозначили ρ(λ) и назвали спектральным коэффициентом отражения. Однако отражение – явление сложное. Часть света отражается зеркально, по закону «угол падения равен углу отражения». Как мы уже говорили, зеркально отраженный свет не дает информации об отражающем предмете.

Нас интересует только рассеянный, диффузно отраженный свет, и под ρ мы будем подразумевать коэффициент диффузного отражения. Но и зтот коэффициент зависит не только от длины волны, но и от угла падения света γ на поверхность тела, от угла отражения γ1 от телесного угла ω, в котором мы собираем рассеянный свет. Коэффициент, учитывающий влияние γ, γ1 и ω на ρ, называется апертурным коэффициентом отражения и обозначается символом β, а спектральный апертурный коэффициент отражения будет β(λ).

14.3. Измерение спектрального апертурного коэффициента отражения.

Схема, поясняющая метод измерения β(λ), изображена на рис. 14.1. Пучок света,

спектральная плотность мощности которого Φωλ (а полная мощность Φωλ dλ), падает под

углом γ на измеряемый образец и, отраженный под углом γ1 проходит через диафрагму и попадает в измерителышй прибор. Диафрагма ограничивает отраженный пучок, пропуская свет только в телесном угле ω. Мощность, подействовавшую на измерительный прибор,

обозначим Φωλ dλ .

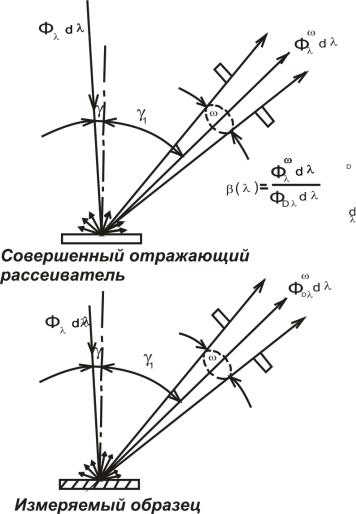
Затем образец заменяют совершенным отражающим рассеивателем D и снова измеряют

мощность ΦωDλdλ , подействовавшую на измерительный прибор. Апертурный коэффициент отражения образца находят как отношение двух измеренных мощностей:

Совершенный отражающий рассеиватель определяется кая идеальный однородный рассеиватель с коэффициентом отражения, равным единице для всех длин волн. Еще в 1760 г. немецкий ученый И. Г. Ламберт (1728–1777) сформулировал закон, согласно которому яркость светорассеивающей поверхности одинакова во всех направлениях. Хотя скоро выяснилось, что закоя Ламберта верен лишь приближенно, он оказался удобен как некая идеализированная модель рассеивающей поверхности. Прибавив сюда еще представление о том, что коэффициент отражения для всех длин воля равен единице, сформулировали свойства совершенного отражающего рассеивателя.

Реального эталона, полностью соответствующего требованиям, предъявляемым к совершенному отражающему рассеивателю, изготовить нельзя. Рабочие пластинки для измерения апертурного коэффициента отражения называют белыми стандартами. Их можно изготовить в виде дисков, спрессованных из оксида магния (MnO) или сульфата бария (BaSO4). Их коэффициент отражения мало отличается от единицы и в пределах видимой дбласти колеблется между 0,970 и 0,985. При точных измерениях эти отклонения эталона приходится учитывать.

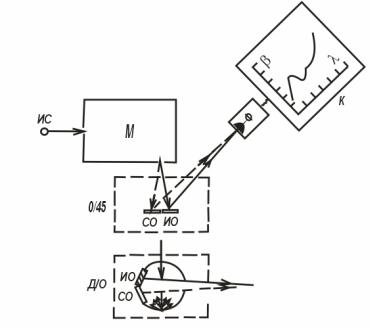
Рис 14.1. Схема измерения спектрального апертурного коэффициента отражения

14.4. Спектрогониофотометр.

Приборы для измерения спектрального апертурного коэффициента отражения называются спектрогониофотометрами. Структурная схема регистрирующего спектрогониофотометра изображена на рис. 14.2. Свет от источника ИС через монохроматор М направляется на пластинку совершенного отражателя СО, и отраженная часть света попадает на фотоэлемент Ф, сигнал от которого поступает в компьютер К. Монохроматор подает на СО последовательно излучения всех длин волн видимого диапазона через малые интервалы ∆λ. Приемник регистрирует приходящие к нему сигналы. Затем па место совершенного отражателя ставится испытуемый образец ИО и рсгистрация повторяется. Прибор автоматически делит данные второн запыси на данные псрвой и выдает зависимость β(λ) либо в виде кривой (схематнчески изображснмой на рисунке), либо в виде цифровой записи. Следуст заметить, что плоскость угла отражсння в общем случае отнюдь не должна совпадать с плоскостыо угла падения. Между ними может быть азимутальный угол α, который значитсльно усложняет измсрения спектрального апертурного коэффициента отражения.

Рис. 14.2. Структурная схема регистрирующего спектрогониофоометра.

14.5. Стандартные условия измерений.

Мы видим, что спсктральпый апертурный коэффициснт отраженпя ρ(λ), будучи сам функцией длины волны, зависит еще от четырех параметров: угла падсния γ, угла отражсния γ1, азимута α и телесного угла отраженного пучка ω. Если каждому параметру придать, скажем, по 20 дискретных зпачеиий и провести измерения для двадцати длин волн, то для определения β(λ) придется сделать более 205, т. е. более трех миллионов, измерений. Поэтому условия измсрения β(λ) стаидартизировали, ограничившись только четырьмя вариантами. Каждый вариант получил свое условное обозначение, которое ыы указываем перед его описанием (рис. 14.3).

1 (0/45). Образец освещается пучком, ось которого составляет с нормалью к поверхности образца угол не более 10°. Образец наблюдается под углом 45 ± 5° к нормали.

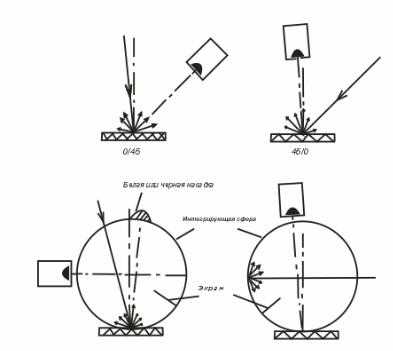
Угол между осью пучка и любым из лучей пучка не должен превышать 10° как в освещающем пучке, так и в пучке наблюдения.

Рис. 14.3. Стандартные варианты измерения спектрального апертурного коеффициента отражении.

2 (45/0). Образец освещается одним или несколькими пучкамк, оси которых составляют угол 45 ± 5° относительно нормали к поверхности образца. Угол между направлением наблюдения и нормалью не должен превышать 10°. Угол между осыо освещающего пучка и любым его лучом не должен превышать 10°. Угол между осью наблюдаемого пучка и любым его лучом тоже не должен быть больше 10°.

В условиях 1 и 2 не оговорены телесные углы ш пучка наблюдения. Но условие, что ни один из лучей пучка не должен отходить от оси более чем на 10°, ограничивает угол ω. Конечно, значения ω для наблюдения измеряемого образца и белого стандарта одинаковы. А пока телесный угол невелик, он мало влияет на результат измерения.

3(0/Д). Образец освещается пучком, ось которого составляет с нормалью к образцу угол не более 10°. Угол между осью освещающего пучка и любым его лучом не должен превышать 5°. Отраженный пучок собирается с помощыо интегрирующей сферы. Она может иметь любой диаметр, но суммарная площадь отверстий в ней не должна превышать 10% ее внутренней поверхности. Введение добавочных белых экранов, изображенных на рис. 14.3, улучшает равномерность засветки интегрирующей сферы.

4(Д/0). Образец освещается диффузно с помощью интегрирующей сферы. Угол между нормалью к образцу и осью пучка не должен превышать 10°. Угол между осью наблюдаемого пучка и любым его лучом не должен превышать 5°.

Формула (14.1) показывает, что спектральный апертурнын коэффициент отражения зависит от телесного угла ω. Укажем два предельных случая. Если ω стремится к нулю, то апертурный коэффициент начинает соответствовать определенному направлению отраженного света и называется в этом случае спектральным коэффнциентом яркости. Если, наоборот, ω стремится к 2π стерадиан (т. е. охватывает всю полусферу над поверхностью образца), спектральный апертурный коэффициент отражения называют спектральным коэффициентом отражения и обозначают ρ(λ).

14.6. Глянец.

Многие предметы часть падающего на них света отражают зеркально, и мы видим, что на их поверхности выделяются более яркие пятна. Такая примесь зеркального отражения называется глянцем. Как мы уже говорили, зеркальное отражение не характеризует свойств самого отражающего предмета, его цветность. Поэтому при измерении спектрального апертурного коэффициента отражения влияние глянца нужно исключить. При первых двух стандартных условиях измерения β(λ) с помощью спектрогониофотометра зеркально отраженный свет исключается сам собой, так как угол падения света на образец не равен углу наблюдения.

При четвертом условии освещение диффузно, и поэтому само понятие угла падения света теряет смысл.

Наконец при третьем условии против зеркального отражения приходится принимать специальные меры. В том месте шара, куда попадает зеркально отраженный от образца свет, ставится так называемая зеркальная ловушка. Она изображена в верхней части шара на рис. 14.3 (черная насадка), Если измерение ведется по варианту 4, вставляют белую втулку и эта часть шара не отличается от всей остальной его поверхности. При варианте 3 втулку делают черной и зеркалыю отраженный свет гасится на ней. Меняя черную втулку на белую, в третьем варианте можно учесть влияние зеркальной части отражения измеряемого образца.

Нужно сказать, что глянец имеет большое значение для внешнего вида многих товаров и поэтому при контроле их качества необходимо его измерять или хотя бы както оценивать.

Зеркало можно характеризовать как поверхность, имеющую максимальный глянец. У поверхности, отражающей свет по закону Ламберта, глянец равен нулю. Все другие поверхности имеют промежуточный глянец. Необходимость оценивать глянец не позволяет ограничить определение спектрального апертурного коэффициента отражения одним из четырех стандартных способов или даже всеми четырьмя. Ведь только третий позволяет както оценить влияние зеркального отражения на β(λ).

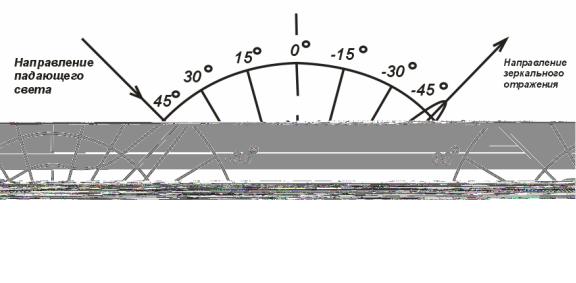
Рис.14.4. Диаграмма распределения интенсивности отражения от образца с гляецем

Совершенно ясно, что глянец больше всего влияет на апертурный коэффициент отражения только тогда, когда падающий и отраженный лучи лежат в одной плоскости. В таком случае обычно и измеряют β(λ) как функцию угла отражения. На рис. 14.4 изображен график зависимости апертурного коэффициента отражения при некоторой фиксированной длине волны. Полуокружность изображает график зависимости β(λ) от угла отражения γ1 для совершенного отражающего образца. Кривая с пиком отражения – график ρ(λ) для полуглянцевого образца. Для совершенного отражателя β(λ) = 1 независимо от угла γ1 Для

глянцевой поверхности вблизи направления γ1 соответствующего зеркальному отражению, выделяется пик интенсивностн, в котором значение β(λ) > 1. И если даже не измерять β(λ) в плоскостях, в которых не лежит γ1 график нужно снять при нескольких значениях γ.

Вырабатывают инструкции для измерения глянца, в основном сводящиеся к указаниям, при каких углах падения производить измерения. Соответственно существуют разные конструкции глянцемеров.

14.7. Вещества, пропускающие свет.

Когда свет проходит сквозь вещество в той или иной мере прозрачное, происходит ряд процессов, вследствие которых мощность прошедшего пучка Ф оказывается меньше мощности пучка, входящего в слой вещества Ф0.

Будем считать, что слой вещества ограничен двумя параллельными плоскостями, причем пучок с мощностью Ф0 падает на одну повёрхность слоя нормально, а с мощностью Ф выходит из слоя, сохраняя свое направление. Ослабление пучка происходит по трем причинам: вследствие отражения от двух поверхностей, ограничивающих слой; из-за поглощения внутри слоя; из-за рассеяния' внутри слоя.

Рассмотрим сначала вещество, не рассеивающее света. Выделим внутри его две плоскости на расстоянии h друг от друга. Поток, входящий в первую плоскость, назовем Ф1

где k – натуральный показатель поглощения среды, а h – толщина слоя.

Если произведение kh = 1, то e–kh = 1/e, а значйт, h – такая толщина слоя, проходя которую, свет ослабляется в е раз т. е. в 2,72 раза. Коэффициент отражения на границе двух сред зависит от отношения их показателей преломления, от угла падения света на поверхность раздела и от поляризации падающего света. Если рассматриваемый нами слой вещества с показателем преломления n окружен воздухом, вместо отношения показателей преломления можно взять просто n, так как показатель преломления воздуха близок к единице. Но если слой поглощает свет, при расчете коэффициента отражения r нужно учесть

где χ = 4λπ k – главный показатель поглощения.

Видно, что вследствие поглощения коэффициент отражения увеличивается. Если χ>>n, величинами (n – 1)2 и (n + 1)2 можно пренебречь по сравнению с χ2n2 и мы получим r = 1. Металлы, поглощение в которых очень велико, действительно обладают большим коэффициентом отражения.

Нас, однако, интересуют сейчас вещества, достаточно прозрачные, пропускающие значительную часть света. Для таких веществ можно пренебречь величиной χ. по сравнен'ию

Для воды n = 1,34; для стекла n = 1,55; отсюда получаем: для воды r = 0,021; для стекла r = 0,047.

При выходе из слоя воды или стекла происходит еще одно отражение. Следовательно, вследствие отражений при переходе сцвозь слой воды свет ослабеет примерно на 4%, а сквозь слой стекла – примерно на 9%. Эти потери на отражение следует учитывать при измерении пропускания. Однако иногда важно только знать, какую часть света пропускает слой; причина ослабления при этом неважна. Если к слою подошел поток Ф0 а вышел поток Ф, коэффициент пропускания можно найти по формуле

разлагает свет на два пучка, поляризованные во взаимно перпендикулярных направлениях. Один пучок уходит в сторону, другой, проходя через призму Волластона, опять раздваивается, и каждый из двух пучков идет в шар через свою щель. Один пучок освещает исследуемый объект, другой – совершенный рассеиватель. Интенсивность каждого из пучков зависит от того, как повернута призма Рошона. При ее вращенни один пучок удваивается, другой ослабевает. При каком-то угле поворота призмы Рошона интенсивность света, отраженного исследуемым предметом, IП и интенсивность света, отраженного совершенным рассеивателем, IC оказываются равными.

Сразу после призмы Л2 поставлен обтюратор (не изображен на схеме), вращающийся со скоростью 25 об-с и пропускающий свет то на исследуемый предмет, то на совершенный рассеиватель. В стенку шара вставлено молочное стекло МС, за которым поставлен фотоэлемент ФЭ. Фототок фотоэлемента пропорционален освещенности молочного стекла Е.

Угол поворота призмы Рошона б будем отсчиты-вать от такого ее положения, при котором освещен-ность совершенного рассеивателя (при открытом для него обтюраторе) равна нулю. Обозначим Еп освещенность молочного стекла в том случае, когда обтюратор пропускает свет на измеряемый предмет, и Ес – освещенность молочного стекла, когда обтюратор пропускает свет на совершенный рассеиватель. Напишем формулы для этих

Здесь рп и рс – коэффициенты отражения исследуемого предмета и совершенного рассеивателя; а – коэффициент, одинаковый в обеих формулах. При равенстве

Приближенно рс (λ) для всех длин волн можно принять за единицу, а можно принять в расчет и точное значение рс(λ) эталона. Так или иначе, спектральный коэффициент отражения исследуемого предмета рп(λ) измерен и может быть вычислен.

Но прибор автоматизирован, и вычислений производить не требуется. Вращение обтюратора приводит к тому, что, пока Е„^ЕС, напряжение на нагрузке имеет перемениую составляющую с частотой 50 Гц. Пока переменная составляющая существует, ток от усилителя У с помощью реверсивного двигателя М1, редукторов Р1 и Р2 и кулачка К1 поворачивает призму Рошона до тех пор, пока переменная составляющая не станет равной нулю.

Поворот призмы Рошона механически связан с пе-ремещением пера П, движущегося вдоль образующей барабана Б. Другой двигатель (М2) с помощью редуктора Р3 и кулачка К2 передвигает щель Щ2 для записи рп(λ) при следующей длине волны. На вра-щающемся барабане закрепляется бланк, на кото-ром и вычерчивается график зависимости рп(λ) от λ,.

Интервалы между соседними длинами волн, при которых измеряется рп(λ), лежат в пределах при од-ном режиме от 0,6 до 1,4 нм, при другом – от 1,2 до 2,8 нм.

Спектрофотометром СФ-18 можно измерять и крэффициент пропускания жидкостей либо твердых пластинок, для которых предусмотрено место между линзой Л2 и призмой ПП. Для жидкостей имеется специальная кювета. Измерения можно проводить по двум шкалам, получая либо коэффициент пропускания τ(λ), либо оптическую плотность D(λ) образца,

Глава 15. Колориметрические расчеты.

15.1. Предварительные замечания.

До сих пор в разных местах книги мы встречались с различными формулами и таблицами для расчета тех или иных величин, связанных с колориметрией, определением цвета, цветности и т. д. Здесь мы хотим сосредоточить эти, ранее несколько разрозненные данные и коснуться не только существа дела, но отчасти и техники расчетов.

15.2. Система RGB.

Напомним, что в системе RGB за основные стимулы приняты три монохроматических излучения с длинами волн: λR = 700 нм, λG = 546,1 нм, λB = 435 нм. Базисный стимул – белый равноэнергети-ческий цвет, который получается, если сложить по одной единице основных цветов R, G и В. Единицы основных цветов имеют разные яркости, отношения которых друг к другу определяются формулой (8.32). Координаты цвета r', g' и b', если известно спектральное распределение мощности излучения Рλ, вычисляются по формуле (6,8) с помощью ординат кривых сложения из табл. 6.1,

В стандарте ГОСТ 13088–67 кривые сложения определяются как координаты монохроматических излучений единичной мощности, т, е. их размерность Вт-1.

Принципиально ничего не изменится, если вместо мощности Р поставить энергетическую яркость Lе, ибо Р и Lе – величины пропорциональные, а если мощность Р излучается с единицы площади и в еди-нице телесного угла, – то и численно равные. Правда, размерность ординат кривых сложения будет уже не просто Вт-1, а Вт-1·м-2·ср-1, так как координаты цвета безразмерны. Обозначим спектральную плотность энергетической яркости Leλ. По аналогии с формулами (6.8) можно написать выражения для координат цвета, вычисленных по плотности энергетической яркости:

Так как Leλ = aPλ, где коэффициент пропорциональности имеет размерность ср-1·м-2, то можно сказать, что, если координаты цвета по формуле (6.8) характеризуют цвет, отнесенный к одному ватту мощности, то координаты, найденные по формулам (15.1), относятся не только к одному ватту, но и к одному стерадиану и одному метру квадратному. Поэтому формулы (6.9) удобнытдля вычисления светового потока Ф, а формулы (15.1) – для вычисления яркости.

За основу вычисления светового потока или яркости в качестве коэффициента К примем значение Кm = 683 лм/Вт, установленное 16-й Генеральной конференцией по мерам и весам в 1979 г. Но поскольку расчеты координат цвета по формулам (6.8); уже отнесены к одному ватту, будем вместо Кm писать Kп = 683 лм. Аналогично для расчета яркости будем применять коэффициент Кя = 683 кд-м-2 (поскольку размерность яркости кд·м-2 = лм·м-2·ср-1).

Решим простейший пример. Пусть излучение равномерно распределено в интервале от λ = 495 нм до λ = 505 нм. Спектральная энергетическая яркость в зтом интервале тоже постоянна: Leλ = 6 Вт·м-2×ср·нм-1. Благодаря узости интервала и равномерному распределению спектральной яркости в нем вместо интеграла можем написать

r′ = Leλ r (λ) λ; g′ = Leλ g(λ) λ; b′ = Leλb (λ) λ .

Найдя в табл. 6.1 значения ординат сложения для λ = 500 нм и подставив λ = 10 нм, получим координату

r′ = 6 Вт•м-2•ср-1 (–0,0713 Вт-1•м2•ср•нм-1) × 10 нм = –6•0,07173•10 = –4,3038.

Аналогично получим g′ = 5,1216 и b' = 2,8658.

Найдем теперь по формуле (8.35) яркость цвета L(Ц) с такими координатами. Положим Кя численно равным Кm, т. е. 683 кд·м-2, как наиболее принятое. Перепишем формулу (8.35) в виде