
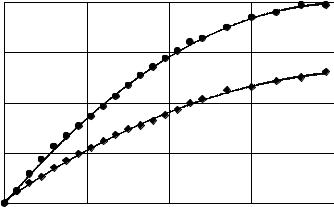
режима так, как показано на рис. 3.7. Для перевода значений термоЭДС в |
|
градусы, принимая начальную температуру подложки равной нулю, исполь- |
|
зовать формулу Т70(120) [K] = Т70(120) [мВ] / 0.0405. |
|
T, К |
1 |
|
|
|
2 |
0 |
t, с |
|
Рис. 3.7. Зависимость температуры подложки от |
|
времени (ток разряда … , давление аргона …) |
при расстоянии до мишени [мм]: 1 – 70; 2 – 120
5. Выполнить численное дифференцирование всех функций T = f(t) и заполнить табл. 3.7 и 3.8.
В табл. 3.7 и 3.8 приняты следующие обозначения (рис. 3.8): i = 0, 1, 2, …, n – номер измерения (значению i = 0 соответствует начало отсчета
t = 0); ∆ti = ∆ti – ∆ti – 1 – i-й интервал измерения во времени (i = 1, 2, …, n).
|
|
|
|
Таблица 3.7 |
i |
∆ti , с |
Ti0, K |
∆Ti, K |
∆Ti/ ∆ti, K |
1 |
∆t1 |
T10 |
∆T1 |
∆T1/ ∆t1 |
2 |
∆t2 |
T20 |
∆T2 |
∆T2/ ∆t2 |
… |
… |
… |
… |
|
|
|
|
|
|
n |
∆tn |
Tn0 |
∆Tn |
∆Tn/ ∆tn |
|
|
|
|
Таблица 3.8 |
|
i |
∆ti , |
Ti0, |
∆Ti, |
|
∆Ti/ ∆ti, |
|
с |
K |
K |
|
K |
1 |
∆t1 |
T10 |
∆T1 |
|
∆T1/ ∆t1 |
2 |
∆t2 |
T20 |
∆T2 |
|
∆T2/ ∆t2 |
… |
… |
… |
… |
|
|
|
|
|
|
|
|
n |
∆tn |
Tn0 |
∆Tn |
|
∆Tn/ ∆tn |
В данном эксперименте принято значение ∆ti = 15 с, но в общем случае
этот интервал может быть произвольным; T |
= Ti +Ti−1 – центральная точка |
i0 |
2 |
|
i-го интервала изменения температуры (i = 1, 2, …, n); ∆Ti = ∆Ti – ∆Ti – 1 – изменение температуры в i-м временном интервале (i = 1, 2, …, n);
54
∆Ti/∆ti = df (ti)/dt – производная функции T = f (t) в i-м временном интервале
(i = 1, 2, …, n).
6. Результаты, полученные в табл. 3.7 и 3.8, отразить графически (рис. 3.9) в координатах (T, dT/dt) в виде точек (Ti0, ∆Ti/∆ti) для i = 1, 2, …, n. Графики построить для обоих режимов, в которых проводился эксперимент.
T, К |
|
|
|
|
|
Tn |
|
|
|
|
|
Ti |
|
|
|
|
|
Ti0 |
|
|
|
|
|
Ti – 1 |
|
|
|
|
|
T2 |
|
|
|
|
|
T20 |
|
|
|
|
|
T1 |
|
|
|
|
|
T10 |
t1 |
t2 |
ti – 1 |
ti |
tn t, с |
0 |
|||||
|
Рис. 3.8. Вычисление производной по времени |
||||
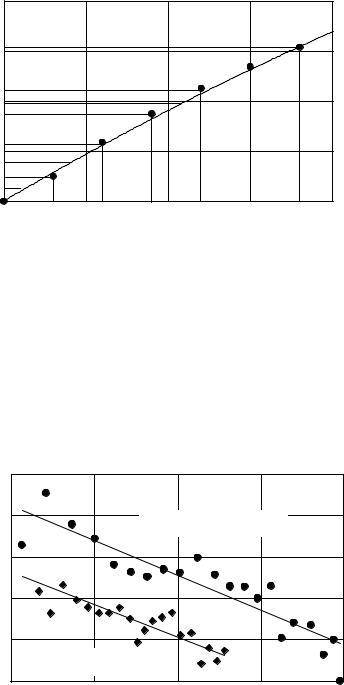
7. Для определения тепловых потоков на подложках в соответствии с (3.16) на полученных в п. 6 графиках построить линии тренда (на рис. 3.9 отображены сплошными линиями) в форме полиномов первого порядка:
dT/dt = aj – bjT, (3.19)
где j = 1, 2, …, 8 – номер экспериментальной зависимости. Для вычисления коэффициентов модели (3.19) использовать метод наименьших квадратов (прил. П.4.3). Значения полученных коэффициентов занести в табл. 3.9.
dT/dt, |
|
К/с |
1. dT/dt = a1 – b1T |
|
|
|
2. dT/dt = a2 – b2T |
0 |
T, К |
Рис. 3.9. Кинетика нагрева подложки при расстоянии |
|
до мишени [мм]: 1 – 70; 2 – 120
55
8. В соответствии с (3.16) тепловой поток на подложке при распылении мишени магнетрона в каждом случае определяется как
|
|
Φ+j |
= A*j = mca j . |
|
|
|
(3.20) |
|||
|
|
|
|
|
|
|
|
Таблица 3.9 |
||
Ток разряда …, |
|
|
|
… |
|
|
|
… |
|
|
давление аргона … |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эксперимент |
Нагрев |
|
Охлаждение |
Нагрев |
Охлаждение |
|
||||
j |
1 |
2 |
|
3 |
4 |
5 |
6 |
7 |
8 |
|
h, мм |
70 |
120 |
|
70 |
120 |
70 |
120 |
70 |
120 |
|
aj, K/с |
|
|
|
|
|
|
|
|
|
|
– bj, 1/с |
|
|
|
|
|
|
|
|
|
|
Φ+j , Вт |
|
|
|
|
|
|
|
|
|
|
Подставить в (3.20) массу подложки m и удельную теплоемкость c для Cu, поскольку в качестве подложек в экспериментах использованы медные
пластинки размером 10×10×1 мм3. Результаты расчета по формуле (3.20) занести в последнюю строку табл. 3.9.
9. Проанализировать полученные результаты, определяя влияние технологических факторов на тепловой поток.
3.4.5. Содержание отчета
1.Цель работы.
2.Схема внутрикамерной технологической оснастки.
3.Вакуумная схема установки.
4.Таблицы с экспериментальными результатами.
5.Основные расчетные соотношения.
6.Таблицы и графики с результатами вычислений.
7.Анализ полученных результатов.
8.Выводы.
3.4.6.Контрольные вопросы
1.За счет каких источников происходит нагрев подложки при магнетронном распылении?
2.Какие процессы приводят к охлаждению подложки?
56
3.В связи с чем происходит рассеяние потока распыляемого вещества мишени?
4.От каких факторов зависит плотность потока распыленного вещества
вплоскости подложки?
5.Как влияет ток разряда на нагрев подложки?
6.Как влияет давление аргона на нагрев подложки?
7.Как влияет давление аргона на охлаждение подложки?
Список рекомендуемой литературы
Данилин Б. С., Сырчин В. К. Магнетронные распылительные системы. – М.: Радио и связь, 1982. – 72 с.
Данилин Б. С. Применение низкотемпературной плазмы для нанесения тонких пленок. – M.: Энергоатомиздат, 1987. – 262 с.
Технология тонких пленок/ Под ред. Л. Майссела. – М.: Сов. радио, 1980. – 125 с.
Шаповалов В. И. Режимы технологических процессов: Учеб. пособие. – СПб.: Кописервис, 2001. – 64 с.
Тумаркин А. В., Шаповалов В. И. Технология тонких пленок: Учеб. пособие. – СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2003. – 64 с.
57
