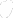Лабы / Лаба 4 / LR4_MalikovBI_0207

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ФЭТ

отчет

по лабораторной работе №4

по дисциплине «ТМиЭЭТ»

Тема: Изготовление пленок методом магнетронного распыления

Студенты гр. 0207 _________________ Маликов Б.И.

_________________ Горбунова А.Н.

Преподаватель _________________ Никитин А.А.

Санкт-Петербург

2023

ЦЕЛЬ РАБОТЫ

Целью работы является изучение процесса изготовления пленок методом магнетронного распыления.

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

Метод магнетронного напыления тонкой пленки основан на физическом распылении рабочего вещества в вакууме. При изучении метода, следует выделить три взаимосвязанных процесса:

– формирование потока рабочего вещества;

– перенос частиц рабочего вещества от источника к подложке;

– формирование пленки на подложке.

Формирование потока рабочего вещества

Среди плазменных систем, в которых для формирования потока рабочего вещества используют физическое распыление, магнетронные распылительные системы (МРС) имеют ряд преимуществ:

– процесс идет при давлении плазмообразующего газа р = 0.1…1 Па, которое ниже, чем в диодных и тетродных системах;

– скорость распыления рабочего вещества можно изменять в широких пределах;

– рабочее напряжение обычно не превышает значения 1 кВ. В диодных и тетродных системах это напряжение в 3–5 раз выше;

– имеется возможность осаждать пленки оксидов, нитридов и других бинарных соединений. Для этого достаточно при распылении металлической мишени ввести в газовую среду химически активный газ;

– с помощью линейных МРС, имеющих длину до 3 м, можно получить пленки с высокой степенью однородности на больших площадях;

– в потоке рабочего вещества отсутствует капельная фаза;

– технологический процесс имеет высокую воспроизводимость;

–на базе магнетронных распылительных систем могут быть созданы полностью автоматизированные установки для нанесения покрытий.

Магнетрон (рисунок 1) помещают в вакуумную камеру, которую откачивают до высокого вакуума. После этого в нее вводят рабочий газ (обычно аргон), доводя его давление до 0.1…1 Па, и подают напряжение U_м между катодом и анодом. В результате между ними возникает аномальный тлеющий разряд, порождающий ток I_р.

Риc. 1 – Схема планарного магнетрона

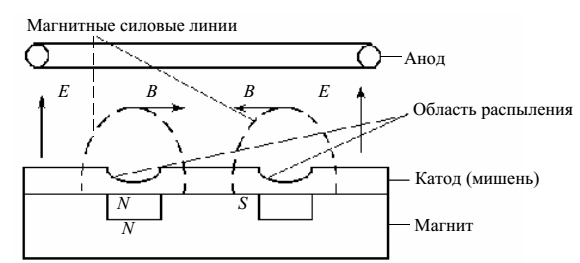
При низком давлении в магнетроне (рис. 2) разряд поддерживается только за счет вторичных электронов, эмитируемых в результате ионной бомбардировки с катода. Эти электроны ускоряются в области темного катодного пространства (ТКП) шириной d_к и движутся по траекториям, близким к циклоидным.

Траектории электронов формируются за счет скрещенных электрического и магнитного полей. Циклоидные траектории возникают только в однородных и ортогональных полях. Конструкция магнетрона обычно такова, что поля E и B неоднородны и не являются ортогональными во всех точках пространства.

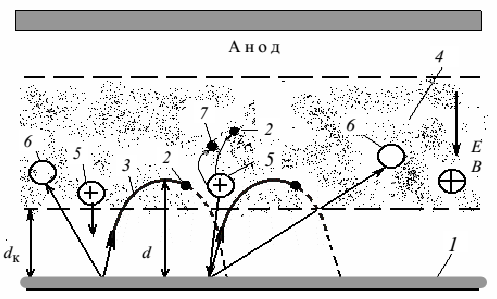
Рис. 2 – Схема магнетронного разряда

Вторичные электроны, получив высокие энергии, входят в область плазмы 4, удаляясь от катода на максимальное расстояние d > d_к, попадают в магнитную ловушку, где совершают неоднократные акты ионизации при столкновении с атомами аргона. Ионизацию за счет электронного удара описывают уравнением Ar + e^– → Ar⁺ + 2 e^–.

Вторичные электроны 2 в каждом акте ионизации теряют энергию, порождая вторичный электрон 7, энергии которого обычно недостаточно для ионизации, поэтому он за счет диффузии перемещается в область анода. Ионы аргона, ускоряясь в области ТКП за счет катодного падения напряжения U_к, бомбардируют катод 1, выбивая из него атомы рабочего вещества 6 и вторичные электроны 2. Электроны 2, энергия которых уменьшилась до тепловой, попадают на анод за счет диффузии в плазме. При аномальном тлеющем разряде можно считать, что все напряжение, приложенное к электродам, падает на ТКП, т. е. U_к ≈ U_м.

Плазма аномального тлеющего разряда в магнетроне локализована за счет магнитного поля в области катода. Степень ионизации плазмы в пространстве можно оценить по профилю распыленной области катода. Связь между величинами I_р и U_м определяет вольт-амперная характеристика (ВАХ).

Рис. 3 – Упрощенная схема распределения рабочего напряжения в устройстве магнетронного распыления

На рис. 3 изображена упрощенная схема распределения рабочего напряжения U_pаб в устройстве магнетронного распыления. К магнетрону (на рис. 3.3 изображен в виде пластины) подключают минус источника питания. Для ограничения тока разряда в цепь включено балластное сопротивление R_б. Для цепи питания справедливо уравнение:

^U_раб ^=U_б ^+U_м ⁽¹⁾

где U_б – напряжение, падающее на балластном сопротивлении; U_м – падение напряжения на магнетроне. Если известна ВАХ магнетрона, то можно записать:

^U_раб ^{= U}_м ^{+ f(U}_м^)R_б (2)

Для узкого диапазона изменения напряжения U_м ВАХ с высокой точностью можно аппроксимировать линейной зависимостью:

^I_р ^=a+bU_м ⁽³⁾

где a и b – известные коэффициенты. Учитывая (1) и (2), выражение (3) можно преобразовать к следующему виду:

_{Iр = (a + bUраб)/(1+bRб) (4)}

Поток рабочего вещества пропорционален мощности разряда I_рU_м. Тогда выражение (4) указывает на то, что при постоянной индукции магнитного поля скорость роста пленки в МРС зависит от трех параметров: тока разряда, напряжения источника питания и номинала балластного сопротивления.

Увеличение тока разряда приводит к росту плотности ионного тока на мишень и, соответственно, к росту скорости распыления. Физическое распыление количественно описывают коэффициентом распыления S = f(E₀, θ), который задает количество атомов, распыляемых одним ионом, и зависит от энергии иона E₀ и угла его падения на поверхность источника вещества θ (θ отсчитывают от нормали к поверхности). При известном значении S плотность потока рабочего вещества в плоскости источника [м²·с]^–1 определяют по формуле:

J₀ = jS/e (5)

где j – плотность ионного тока, А/м²; e =1.6·10^–19 Кл – заряд электрона.

Массовый поток [кг/м²·с] с учетом (5) описывается выражением:

I_m0 = jSM/eN_A (6)

где M – молярная масса материала мишени, кг/кмоль; = 6.02·10²⁶ кмоль⁻¹ постоянная Авогадро.

Перенос рабочего вещества

Средняя энергия частиц в потоке при распылении лежит в пределах 3…5 эВ. Магнетрон обычно работает при давлении аргона, которое выше 1 мТорр. В этом случае средняя длина свободного пробега частицы L_T,p будет не больше 47 мм.

Формирование пленки на подложке

Для потока частиц с энергией несколько электрон-вольт термодинамическая модель формирования пленки на подложке становится не вполне адекватной. В этом процессе возникает сильно неравновесная система со значительным избытком энергии. На начальной стадии роста могут образовываться переходные слои за счет перемешивания материалов пленки и подложки.

Нагрев подложки при напылении пленки

Процесс осаждения пленки на подложку при физическом распылении сопровождается ее нагревом за счет:

– кинетической энергии атомов осаждаемого материала;

– тепла, выделяемого при конденсации и кристаллизации;

– кинетической энергии нейтрализованных и отраженных от мишени атомов рабочего газа;

– энергии вторичных электронов с мишени;

– излучения плазмы;

– излучения нагретой поверхности мишени;

– выделения теплоты экзотермической химической реакцией, протекающей на подложке с участием рабочего вещества.

Рис. 4 – Тепловые потоки на поверхности подложки (1)

с держателем (2) при формировании пленки (3)

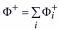Полный поток тепла на подложке (показан на рис. 4 одной стрелкой) [Вт = Дж/c] в любом технологическом процессе определяется как:

(7)

где Φ_i⁺ – тепловой поток на подложке, возникший за счет i-го процесса.

Одновременно с нагревом подложка охлаждается через поверхность за счет:

– излучения;

– теплопроводности газа;

– теплопроводности элементов конструкции держателя подложки;

– поглощения теплоты эндотермической химической реакцией, протекающей на подложке с участием рабочего вещества.

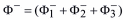Потоки тепла, приводящие к охлаждению подложки, показаны на рис. 4 несколькими стрелками. Полный охлаждающий поток на подложке, нагретой до температуры T, в пренебрежении химической реакцией имеет вид:

(8)

где Φ₁⁻ ~ T ⁴, Φ₂⁻ ~ T и Φ₃⁻ ~ T – потоки тепла, возникшие за счет излучения, теплопроводности газа и теплопроводности элементов конструкции держателя подложки соответственно.

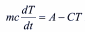C учетом того, что максимальный нагрев подложки при формировании пленки не превышает 400...450 K, излучением можно пренебречь, и положив в B = 0, получим:

(9)

Из (9) следует, что существует возможность экспериментально определить поток Φ⁺. Для этого достаточно при распылении мишени выполнить измерение зависимости температуры подложки от времени:

T^* = f(t) (10)

где знак «*» указывает на то, что результат является экспериментальным.

СХЕМА ИЗМЕРИТЕЛЬНОЙ УСТАНОВКИ

Рис. 5 – Компьютерная модель технологической установки

ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

Табл. 1

При R = 250 Ом
U, кВ	0,5	0,6	0,7	0,8	0,9	1
v, мкм/мин	0,1255	0,1925	0,2719	0,3596	0,4610	0,5883

Табл. 2

При U = 0,6 кВ
R, Ом	100	150	200	250	300
v, мкм/мин	0,8026	0,5102	0,3194	0,1897	0,1

По полученным экспериментальным значениям получим графики зависимости скорости роста пленки от значения рабочего напряжения и от значения балластного сопротивления:

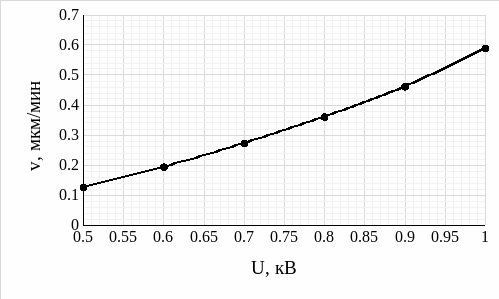
Рис. 6 – График зависимости скорости роста пленки от значения рабочего напряжения

Рис. 7 – График зависимости скорости роста пленки от значения балластного сопротивления

Вычислим зависимость скорости роста пленки от значения тока. Значение силы тока определим из закона Ома:

Табл. 3

При R = 250 Ом
U, кВ	0,5	0,6	0,7	0,8	0,9	1
I, А	2	2,4	2,8	3,2	3,6	4
v, мкм/мин	0,1255	0,1925	0,2719	0,3596	0,4610	0,5883

Табл. 4

При U = 0,6 кВ
R, Ом	100	150	200	250	300
I, A	6	4	3	2,4	2
v, мкм/мин	0,8026	0,5102	0,3194	0,1897	0,1

Пример вычисления значения тока при R = 250 Ом и U = 0,6 кВ:

I = 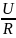= = 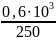2,4 А

Построим графики зависимостей скорости роста пленки от значений тока при R = const = 250 Ом и U = const = 0,6 кВ:

Рис. 8 – График зависимости скорости роста пленки от значения тока при R = const = 250 Ом

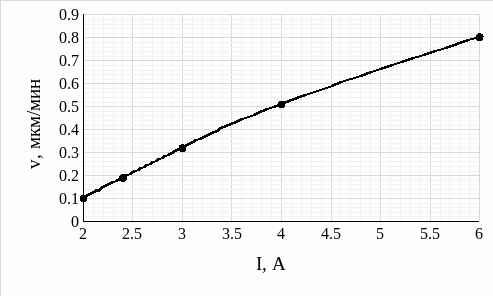
Рис. 9 – График зависимости скорости роста пленки от значения тока при U = const = 0,6 кВ

ВЫВОД

В ходе проведения данной лабораторной работы, были получены экспериментальные данные, на основании которых можно сделать следующие выводы:

Анализируя график зависимости скорости роста пленки от значения рабочего напряжения (рис. 6) и график зависимости скорости роста пленки от значения тока при R = const = 250 Ом (рис. 8), делаем вывод, что при увеличении рабочего напряжения при постоянном сопротивлении (то есть при увеличении рабочего тока) скорость роста пленки значительно увеличивается, а именно, если рассматривать крайние значения диапазона рабочих напряжений (0,5 кВ и 1 кВ), скорость роста пленки увеличилась в 0,5883/0,1925 = 4,69 раз при увеличении напряжения в 2 раза.

Также, анализируя график зависимости скорости роста пленки от значения балластного сопротивления (рис. 7) и график зависимости скорости роста пленки от значения тока при U = const = 0,6 кВ (рис. 9), делаем вывод, что при увеличении значения балластного сопротивления при постоянном напряжении скорость роста пленки уменьшается. То есть, при уменьшении рабочего тока скорость роста пленки также уменьшается. Так, при увеличении балластного сопротивления в 3 раза (100 Ом – 300 Ом), значение скорости роста пленки уменьшилось в 0,8026/0,1 = 8 раз.