Лабы Кондрашов / Лаба 4 / 0207_lab4_Маликов

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ФЭТ

отчет

по лабораторной работе №4

по дисциплине «Физические основы функциональной электроники»

Тема: Исследование параметров СВЧ-фильтров на бегущих спиновых волнах

Студенты гр. 0207 _________________ Маликов Б.И.

_________________ Горбунова А.Н.

Преподаватель _________________ Кондрашов А.В.

Санкт-Петербург

2024

ЦЕЛЬ РАБОТЫ

Целью лабораторной работы является исследование передаточных характеристик СВЧ-фильтра, построенного на бегущих спиновых волнах (СВ), а также ознакомление с основными принципами конструирования спин-волновых фильтров по заданным техническим характеристикам.

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

Фильтрация является одной из главных функций обработки сигнала. Конструкции фильтров на распространяющихся СВ чаще всего используют многоэлементные антенны (в частном случае – периодические), а также волноведущие пленочные структуры. Типичная конструкция спин-волнового фильтра показана на рисунке 1. Основным элементом СВЧ-фильтра на бегущих СВ является тонкая ферромагнитная пленка, выращенная на диэлектрической подложке:

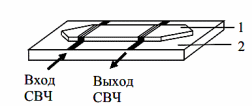
Рисунок 1 – Спин-волновой фильтр с многоэлементными антеннами: 1 – ферромагнитная пленка, 2 – диэлектрическая подложка

Выведем выражение для частотной характеристики передачи сигнала спин-волновым фильтром на многоэлементных микрополосковых антеннах. Рассмотрим процесс формирования амплитудно-частотной характеристики (АЧХ) на простейшем примере фильтра, когда входная антенна содержит всего два элемента, а выходная является одноэлементной. Будем считать, что расстояние между антеннами равно 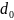, а расстояние между элементами входной антенны равно s. Сигнал, поданный на входную антенну, запишем в виде 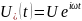. Выходной сигнал можно найти как сумму СВ, излучаемых элементами входной антенны. Каждая волна будет иметь одну и ту же частоту ω, но разные набеги фаз , то есть:

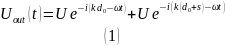
Определяя частотную характеристику фильтра как отношение выходного и входного сигналов , на основании (1) получаем:

АЧХ определяется частотной зависимостью модуля выражения (2). Она равна:

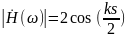
Если учесть потери при распространении СВ между входной и выходной антеннами на пути d₀ и для упрощения пренебречь потерями на пути s, то АЧХ запишется в виде:

На рисунке 2 представлена частотная зависимость 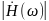, совмещенная с дисперсионной характеристикой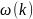 . Для построения АЧХ выбран случай СВ с положительной дисперсией. Физически пульсации можно объяснить как результат интерференции двух СВ, приходящих от каждого из элементов входной антенны на выходную. При изменении частоты разность фаз между этими волнами меняется, и они интерферируют то в фазе (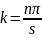 , n = 0, 2, 4, …), то в противофазе ( , n = 1, 3, 5, …). Из-за нелинейности дисперсионной характеристики ширина полос пропускания уменьшается с ростом частоты.

Рисунок 2 – Формирование АЧХ-фильтра с многоэлементными антеннами

Характеристика на рисунке 2 представляет собой набор полос пропускания и заграждения. Как ясно из рисунка, ширина этих полос определяется крутизной дисперсионной характеристики и величиной расстояния между элементами антенн СВ s. Подбирая толщину пленки L, то есть крутизну дисперсионной характеристики и расстояние между элементами антенны, можно регулировать ширину полос пропускания в широких пределах (в сотни раз).

Использование антенн более сложных конструкций позволяет регулировать положение полос пропускания относительно дисперсионной характеристики.

ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА

На рис. 3 показано основное меню программы расчета передаточных характеристик спин-волновых пленочных приборов. В правой части программы находятся пункты, описывающие конструкцию прибора. В первом пункте указываются данные пленки, во втором – параметры антенн.

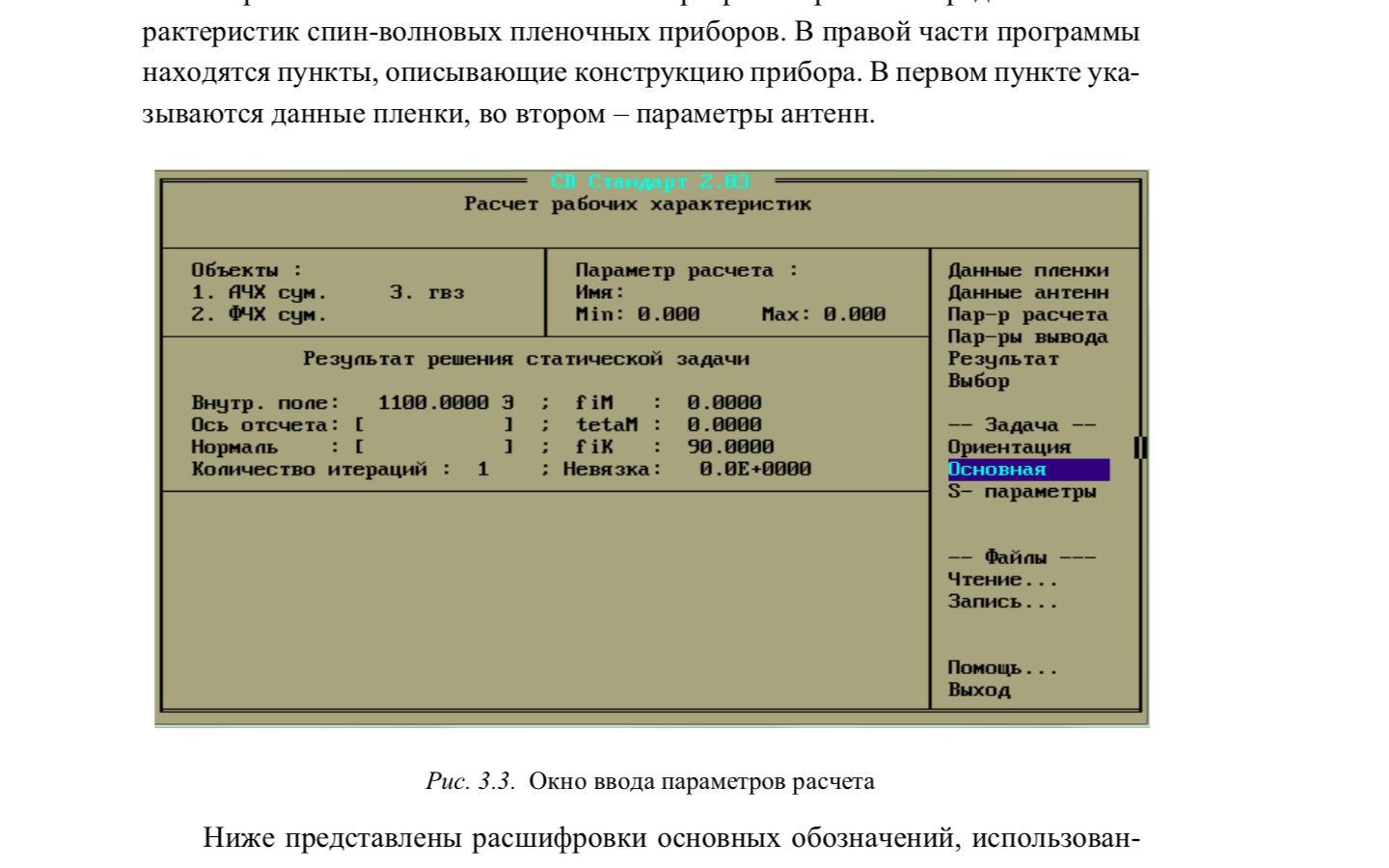
Рисунок 3 – Окно ввода параметров расчета

Ниже представлены расшифровки основных обозначений, использованных в программе расчета.

Данные пленки:

  L – толщина пленки, 0,1–100 мкм;

  a – расстояние до верхнего экрана, > 0 мкм;

  b – расстояние до нижнего экрана, > 0 мкм;

  M₀ – намагниченность насыщения, Гс;

  Не – внешнее магнитное поле, Э;

  На – поле кубической анизотропии, Э;

  Нu – поле одноосной анизотропии;

  dH – ширина линии ферромагнитного резонанса, Э;

  Т – температура, ^оС;

  fi – азимутальный угол внешнего магнитного поля, град;

 teta – полярный угол внешнего магнитного поля, град;

  f0 – азимутальный угол волны, град.

Данные антенны:

  La – длина антенны, мм;

  Ls – расстояние между антеннами, мм;

  Es – диэлектрическая проницаемость подложки;

  Ef – диэлектрическая проницаемость феррита;

  Rs – сопротивление;

  Симм – симметричность антенны;

  wi – ширина i-й антенны, мкм;

  si – смещение i-й антенны, мкм;

  di – зазор пленка–антенна,> a.

ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

1. Исследование передаточной характеристики СВЧ-фильтра на поверхностных спиновых волнах (ПСВ) для трех различных значений толщины пленки при фиксированных параметрах: Н_е = 1750 Э, М₀ = 1750 Гс

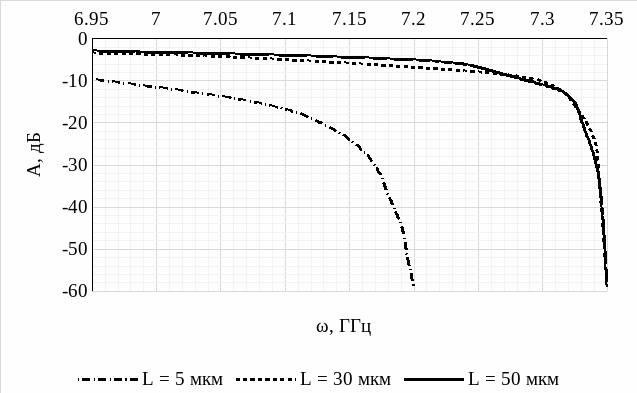
Рисунок 4 – Передаточная характеристика СВЧ-фильтра при различных значениях толщины пленки

Анализируя передаточную характеристику СВЧ-фильтра при различных значениях толщины пленки (рис. 4), делаем следующие выводы:

В первую очередь обратимся к закону дисперсии ПСВ:

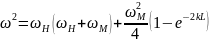
Построим дисперсионную характеристику, а также передаточную характеристику СВЧ-фильтра для разных толщин пленки (L₁ и L₂ > L₁):

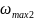
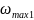
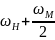
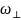
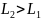
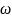
Рисунок 5 – Передаточная характеристика СВЧ фильтра, построенная на основании дисперсионной характеристика ПСВ

Опираясь на рис. 5 можем сказать, что толщина пленки в значительной степени влияет на передаточную характеристику СВЧ-фильтра. Так, более «толстая» пленка имеет более «крутой» характер дисперсионной кривой (следует из закона дисперсии ПСВ, приведенного выше), то есть, групповая скорость в случае «толстых» пленок выше, коэффициент пропускания A также выше. Также, важно уточнить, что вне зависимости от толщины пленки существует критерий предельной ширины полосы возбуждения, который определяется как:

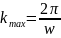
где w – ширина полоска (антенны).

Отсюда следует, что волны короче полоска возбуждать невозможно, соответственно, передаточная характеристика фильтра зависит от значения . То есть, значению для двух толщин пленок (рис. 5) соответствуют два значения частоты: и , которые и определяют предел передаточной характеристики. Так как более «толстая» пленка имеет более «крутую» характеристику, то и значение частоты 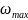будет находиться в более высокочастотной области: , то есть передаточная характеристика «толстых» пленок значительно шире. При этом, передаточная характеристика для двух толщин пленки начинается с частоты , которая в нашем случае равна: = 6,95 ГГц.

2. Исследование передаточной характеристики СВЧ-фильтра на поверхностных спиновых волнах (ПСВ) для трех различных значений напряженности внешнего магнитного поля при фиксированных параметрах: L = 30 мкм, М₀ = 1750 Гс

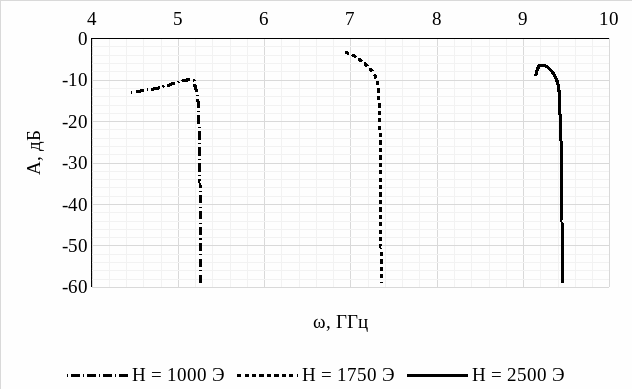
Рисунок 6 – Передаточная характеристика СВЧ-фильтра при различных значениях напряженности внешнего магнитного поля

Анализируя передаточную характеристику СВЧ-фильтра при различных значениях напряженности внешнего магнитного поля (рис. 5), делаем следующие выводы:

Как было рассмотрено в предыдущем пункте, передаточная характеристика СВЧ-фильтра начинается с частоты , которая вычисляется как:

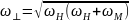, где

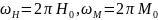
То есть, изменяя значение величины напряженности внешнего магнитного поля мы также изменяем частотный диапазон полосы пропускания СВЧ-фильтра, перемещая его в более высокочастотную область (в случае увеличения значения напряженности внешнего магнитного поля).

При этом, стоит заметить, что мы увеличиваем как нижнюю границу полосы пропускания, так и верхнюю, определяемую для ПСВ как: .

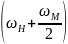3. Исследование передаточной характеристики СВЧ-фильтра для трех основных направлений намагниченности при фиксированных параметрах: L = 30 мкм, М₀ = 1750 Гс, Н_е = 2500 Э

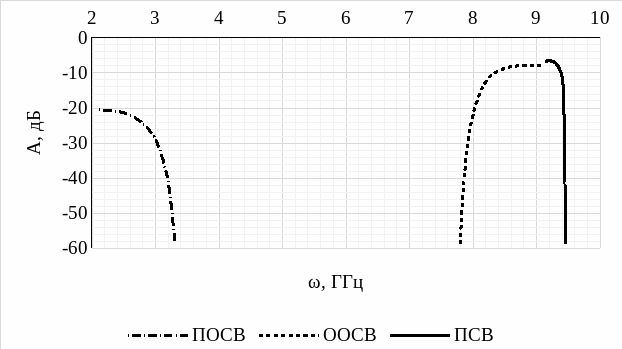
Рисунок 7 – Передаточная характеристика СВЧ-фильтра при различных направлениях намагниченности

Анализируя передаточную характеристику СВЧ-фильтра при различных направлениях намагниченности (рис. 7), делаем следующие выводы:

Передаточная характеристика СВЧ-фильтра при различных направлениях намагниченности в первую очередь зависит от закона дисперсии для каждого из трех типов волн: прямой объемной спиновой волны (ПОСВ), обратной объемной спиновой волны (ООСВ) и поверхностной спиновой волны (ПСВ). Запишем закон дисперсии для каждого типа волны:

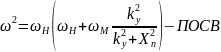
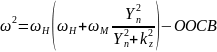
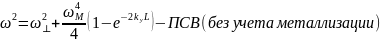
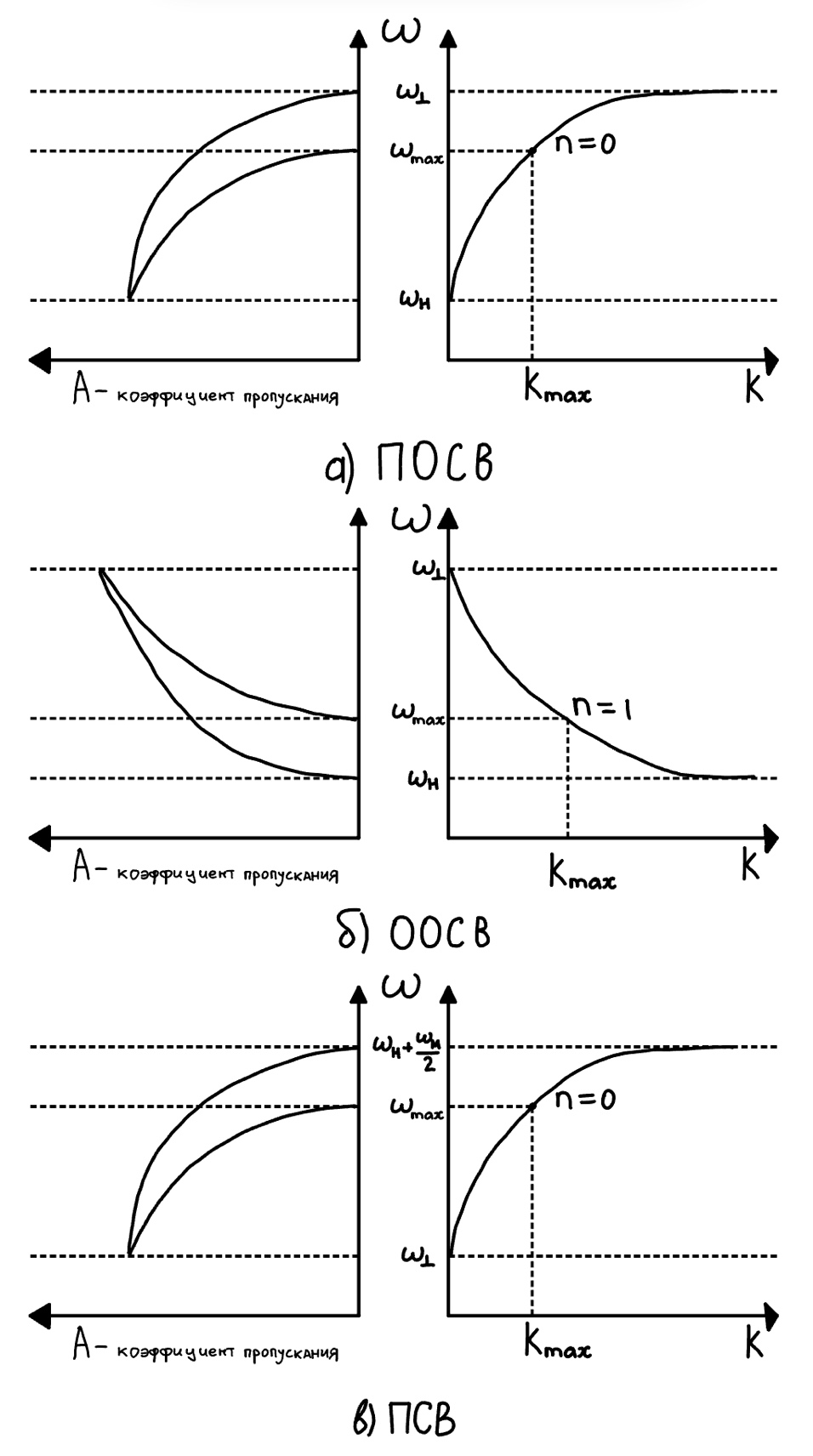
Также, приведем дисперсионные характеристики и построенные на их основе передаточные характеристики для каждого из типов волны:

А

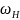
а) ПОСВ

А

б) ООСВ

А

в) ПСВ

Рисунок 8 – Передаточные характеристики СВЧ-фильтра для трех типов волн, построенные на основании их дисперсионных характеристик

Как можно заметить, дисперсионные характеристики для каждого типа СВ значительно отличаются по своему виду. Так, практически одинаковый ход дисперсионных кривых имеют типы волн ПОСВ (рис. 8, а) и ПСВ (рис. 8, в), однако, для данных типов волны характерны свои частотные значения полосы пропускания, что и видим на рис. 7. Для ПСВ выделяем следующий диапазон передаточной характеристики: [9,1 ГГц; 9,5 ГГц]. Для ООСВ (рис. 8, б) имеем совсем иную передаточную характеристику. Что закономерно, если учитывать закон дисперсии данного типа волны и ход дисперсионной кривой (рис. 8). Диапазон передаточной характеристики для ООСВ, соответственно: [7,8 ГГц; 9,1 ГГц].

Однако, важный момент состоит в том, что для ООСВ и ПСВ значение напряженности внешнего и внутреннего магнитных полей равны: H_e = H_i. Но для ПОСВ значение напряженности внутреннего магнитного поля не равно значению напряженности внешнего магнитного поля: H_e = H_i – M_0. То есть, для ПОСВ значение напряженности внутреннего магнитного поля значительно меньше значений напряженности внутреннего магнитного поля ООСВ и ПСВ. Соответственно, передаточная характеристика ПОСВ находится ниже по частоте и для ПОСВ диапазон передаточной характеристики в нашем случае равен: [2,1 ГГц; 3,3 ГГц].

Также, важно уточнить, как было написано ранее, ширина передаточной характеристики определяется значением , которая имеет обратную зависимость от ширины полоска (антенны) w. Соответственно, фактическая ширина передаточной характеристики для трех типов СВ зависит от значения , которая может увеличиваться с уменьшением ширины полоска (антенны).

4. Исследование передаточной характеристики СВЧ-фильтра на поверхностных спиновых волнах (ПСВ) для двухэлементных антенн с различными расстояниями между антеннами при фиксированных параметрах: L = 30 мкм, М₀ = 1750 Гс, Н_е = 2500 Э

Рисунок 9 - Передаточная характеристика антисимметричной антенны при различных расстояниях между элементами антенны

Рисунок 10 - Передаточная характеристика антисимметричной антенны при расстоянии между элементами антенны s = 150 мкм

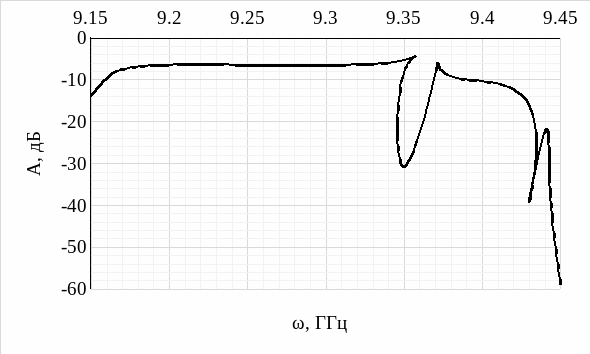
Рисунок 11 - Передаточная характеристика антисимметричной антенны при расстоянии между элементами антенны s = 350 мкм

Рисунок 12 - Передаточная характеристика антисимметричной антенны при расстоянии между элементами антенны s = 600 мкм

Анализируя передаточную характеристику антисимметричной антенны при трех различных расстояниях между элементами антенны (рис. 10, рис. 11, рис. 12), делаем следующие выводы:

Передаточная характеристика многоэлементной антенны, которая, как и описывалось ранее, строится на основании дисперсионной характеристики ПСВ, представляет собой набор минимумов и максимумов, которые определяются синфазным или, соответственно, противофазном сложением волн. Запишем соответствующие условия для двухэлементной антенны:

k = 2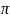 n/s – синфазное сложение

k = ( + 2 n)/s – противофазное сложение

где n = 1, 2, 3…

Соответственно, в случае двухэлементной антенны имеем передаточную характеристику, изображенную на рис. 2.

Однако, в случае антисимметричной антенны передаточная характеристика совсем другая. Так, если представить антисимметричную антенну в следующем виде:

3

2

1

s

ЖИГ

d

Рисунок 13 – Спин-волновой прибор, использующий антисимметричную антенну

Фазы излучающихся волн от каждого элемента входной антенны (1 и 2) к выходной (3) антенне можно представить в виде:

1 3:

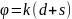
2 3:

То есть, за счет противоположного направления протекания тока фазы волн будут отличаться на , в результате чего «максимумы» и «минимумы» антисимметричной антенны поменяются местами с «максимумами» и «минимумами» на АЧХ двухэлементной антенны (рис. 2). Таким образом, «максимумы» на АЧХ двухэлементной антенны будут соответствовать «минимумам» на АЧХ антисимметричной антенны.

Также, опираясь на условия синфазного и противофазного сложения, приведенных ранее, делаем вывод, что при увеличении расстояния между элементами антисимметричной антенны (s) в значительной степени увеличивается количество «минимумов» и «максимумов», что также следует из дисперсионной характеристики, крутизна которой уменьшается с увеличением частоты.

ВЫВОД

В ходе выполнения данной лабораторной работы были получены передаточные характеристики СВЧ-фильтра на ПСВ при различных параметрах, на основании которых делаем вывод, что при изменении симметрии антенны в значительной степени изменяются передаточные характеристики фильтра: на графике получаем набор «минимумов» и «максимумов». Также, увеличение значения напряженности поля и толщины пленки приводят к уширению частотного диапазона передаточной характеристики.