МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ФЭТ

отчет

по лабораторной работе №1

по дисциплине «Физические основы функциональной электроники»

Тема: Исследование спектра спиновых волн, обладающих положительной дисперсией

Студенты гр. 0207 _________________ Маликов Б.И.

_________________ Горбунова А.Н.

Преподаватель _________________ Кондрашов А.В.

Санкт-Петербург

2024

ЦЕЛЬ РАБОТЫ

Целью лабораторной работы является моделирование и исследование дисперсионных характеристик прямых объемных спиновых волн (ПОСВ) в ферромагнитных пленках и определение дисперсионной характеристики в зависимости от параметров пленки и напряженности внешнего магнитного поля.

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

Рис. 1 - Геометрия задачи о нахождении спектра спиновых волн в нормально намагниченной пленке

Объектом исследования в лабораторной работе является ферромагнитная пленка (плоскопараллельная пластинка) толщиной L, намагниченная до насыщения перпендикулярно ее поверхности вдоль оси z (рис. 1). Считаем, что пленка не ограничена в плоскости ху, а центр прямоугольной системы координат хуz совпадает с центром пленки.

Задача о нахождении спектра распространяющихся в пленке спиновых волн (СВ) сводится к решению уравнения Уокера (1) и уравнения Лапласа (2):

В уравнении Уокера µ – диагональный элемент тензора магнитной проницаемости:

В выражении (3) приняты следующие обозначения:

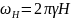
где H – внутреннее магнитное поле; M₀ – намагниченность насыщения ферромагнетика;   2,8 МГц/Э.

Решение дифференциальных уравнений (1), (2) ищем в виде неоднородных плоских волн, распространяющихся вдоль оси у (тогда ):

Сформулируем граничные условия для магнитостатического потенциала (4). Из условий непрерывности тангенциальных составляющих магнитного поля и нормальной составляющей магнитной индукции при z = L / 2 имеем:

Для отыскания спектра магнитостатических волн (МСВ) общее решение уравнения Уокера (1) представим в виде:

а решение уравнения Лапласа (2) – в виде:

Где А, В, С и D – произвольные постоянные, а k_ze – положительная величина. Подстановка решений (8) в уравнение Лапласа дает:

Так как нас интересуют распространяющиеся волны, то 0. С учетом этого, принимая без ограничения общности k_y 0, можно на основании (9) положить:

и тем самым исключить k_ze из дальнейшего рассмотрения.

Обратим внимание на физический смысл соотношения (10). Оно показывает, что поле магнитостатической волны вне ферромагнитной пленки тем сильнее «прижимается» к ее поверхности, чем меньше длина волны . Иными словами, поле коротких волн быстрее спадает от поверхности пленки, чем поле длинных волн. Это полезно помнить при решении практических задач.

Подстановка решения (7) в (1) приводит к характеристическому уравнению:

связывающему продольное k_y и k_z поперечное волновые числа СВ.

Требуя выполнения граничных условий для решений (7) и (8), приходим к системе четырех линейных однородных уравнений относительно неизвестных амплитуд А, В, С и D. Эта система имеет нетривиальное решение, если ее определитель обращается в нуль. Условие равенства нулю определителя системы дает дисперсионное уравнение. Необходимо подчеркнуть, что в силу симметрии граничной задачи для перпендикулярно намагниченной пленки ее решение распадается на два класса: для симметричных (четных по z) и антисимметричных (нечетных по z) волн.

Дисперсионные уравнения для симметричных и антисимметричных волн соответственно имеют вид:

Очевидно, что эти уравнения – трансцендентные. Совместно с характеристическим уравнением (11) и частотной зависимостью (3) они определяют закон дисперсии СВ.

Нетрудно показать, что закон дисперсии можно описать в виде:

где X_n – корни трансцендентных уравнений (12) и (13), определяющие разрешенные (дискретные) значения поперечных волновых чисел k_y.

Спектр МСВ легко построить качественно с помощью (14). Такой спектр показан на рис. 2, а. При , что соответствует , все дисперсионные кривые стягиваются в точку (на «дне» спектра СВ). Дисперсионной кривой, ограничивающей спектр по частоте сверху, отвечает симметричная волна с простейшим распределением магнитостатического потенциала. Эта волна называется основной, или волной низшего типа. Волны более высокого порядка отличаются формой распределения магнитостатического потенциала по толщине пленки.

Рис. 2 – Спектр (а) и групповая скорость (б) объемных спиновых волн в перпендикулярно намагниченной пленке. При расчете принято

Рассмотрим групповую скорость СВ , которую можно найти дифференцированием дисперсионного соотношения (14). Выполнив соответствующие вычисления, можно показать, что групповая скорость максимальна для волны низшего типа и при равна:

Для остальных типов СВ при k_y 0 групповые скорости равны нулю. Экстремальные значения групповых скоростей высших типов СВ, существующие при промежуточных значениях k_y, остаются значительно меньше величины (15) (рис. 2, б).

Различия между групповыми скоростями и их частотными зависимостями для высших и низшего типов СВ приводят к тому, что волны высших типов затухают гораздо сильнее, чем низшего. Поэтому именно волна низшего типа обычно отвечает за перенос энергии СВЧ-сигнала в спин-волновых приборах.

Экспериментальная установка

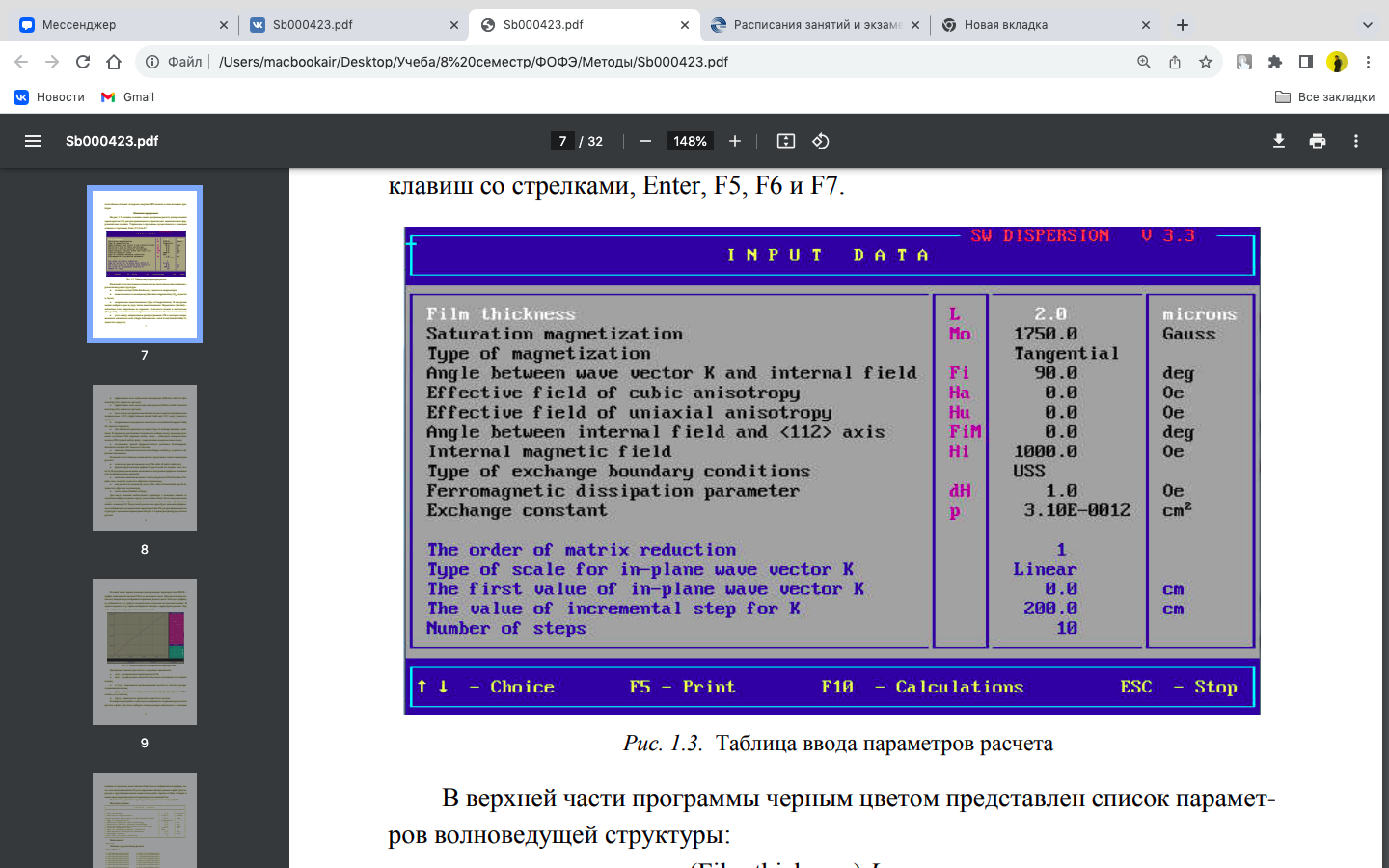
Рис. 3 – Таблица ввода параметров расчета

На рис. 3 показано основное меню программы расчета дисперсионных характеристик СВ, распространяющихся в произвольно намагниченных ферромагнитных пленках. Управление в программе осуществляется с помощью клавиш со стрелками, Enter, F5, F6 и F7.

В верхней части программы черным цветом представлен список параметров волноведущей структуры:

 толщина пленки (Film thickness) L, задается в микрометрах;

 намагниченность насыщения (Saturation magnetisation) M₀, задается в гаусах;  направление намагничивания (Type of magnetization). В программе можно выбрать один из двух типов намагничивания. Нормальное (Normal) – магнитное поле направлено по нормали к плоскости пленки и касательное (Tangential) – магнитное поле направлено по касательной к плоскости пленки;  угол между направлением распространения СВ и вектором напряженности магнитного поля (Angle between wave vector k and internal field) Fi, задается в градусах

 эффективное поле кубической анизотропии (Effective field of cubic anisotripy) Ha, задается в эрстедах;

 эффективное поле одноосной анизотропии (Effective field of uniaxial anisotripy) Нu, задается в эрстедах;

 поле между внутренним магнитным полем и кристаллографическим направлением (Angle between internal field and axis), задается в градусах;

 напряженность внутреннего магнитного поля (Internal magnetic field) Hi, задается в эрстедах;

 тип обменных граничных условий (Type of exchange boundary conditions). В программе реализована возможность выбора между двумя предельными случаями. USS (unpinned surface spins) – свободные поверхностные спины и PSS (pinned surface spins) – закрепленные поверхностные спины;

 полуширина кривой ферромагнитного резонанса (Ferromagnetic dissipation constant) dH, задается в эрстедах;

 значение обменной константы (Exchange constant) p, задается в обратных сантиметрах. В нижней части таблицы синим цветом представлен список параметров расчета:

 количество рассчитываемых мод (The order of matrix reduction);

 формат представления графика (Type of scale for in-plane wave vector k). В программе реализована возможность построения графика в линейном или логарифмическом масштабе;

 начальное значение волнового числа для расчета (The first value of inplane wave vector k), задается в обратных сантиметрах;

 шаг расчета по волновому числу (The value of incremental step for k), задается в обратных сантиметрах;

 число шагов (Number of steps).

Обработка результатов измерений

1. Спектр св и зависимость групповой скорости от частоты для трех различных значений толщины пленки

Приведем исходные значения, при которых производились расчеты: M = 1200 Гс; H = 1800 Э.

1.1 Спектр св для трех различных значений толщины пленки

5040 МГц

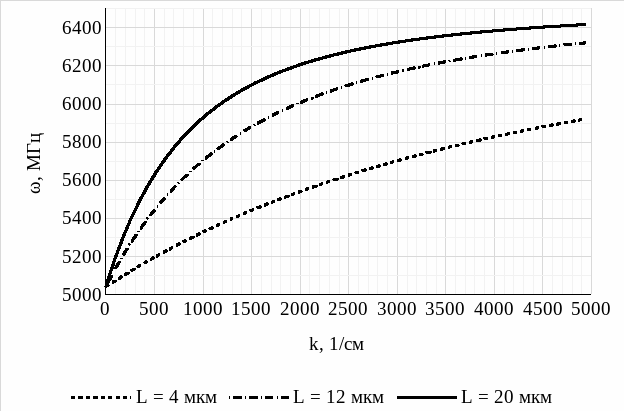
Рис. 4 – Спектр СВ для трех различных значений толщины пленки

(мода n = 0)

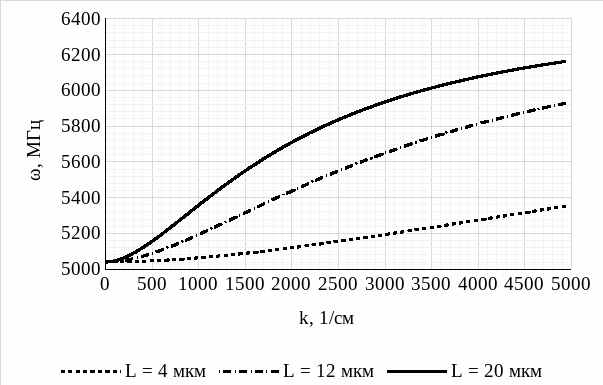
Рис. 5 – Спектр СВ для трех различных значений толщины пленки

(мода n = 1)

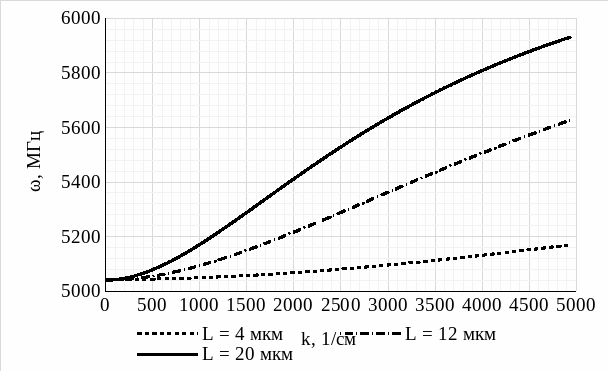
Рис. 6 – Спектр СВ для трех различных значений толщины пленки

(мода n = 2)

Анализируя полученные графики спектра СВ для трех различных значений толщины пленки (L = 4 мкм; L = 12 мкм; L = 20 мкм), построенные для трех мод (n = 0; n = 1; n = 2), делаем следующие выводы:

1. Для каждого из трех построенных спектров СВ заметно стягивание дисперсионных кривых для трех разных толщин пленки в одну точку (частота отсечки). Данная точка соответствует значению частоты: 5040 МГц (для данной работы) и значению продольного волнового числа k_y = 0. Данное свойство следует напрямую из закона дисперсии (14), а именно:

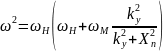
То есть, в случае k_y = 0, получаем: . В нашем случае 5040 МГц, что по своей сути является частотой ферромагнитного резонанса.

Таким образом, при k_y = 0 – случай спин-волнового резонанса с частотой .

Также, стоит заметить, что сверху по частоте дисперсионные кривые ограничены частотой , которую можно вычислить как:

Данная частота выводится из дисперсионного уравнения в случае угла :

где – обменная константа; k – волновое число.

2. С увеличением частоты заметно значительное возрастание волнового числа. Данный вывод также следует из анализа выражения для волнового числа:

Волновое число – число волн на длине 2 . Таким образом, становится более очевидна зависимость волнового числа от длины волны (частоты) – с уменьшением длины волны (увеличением частоты) происходит увеличение волнового числа, то есть, более короткие волны в большем количестве укладываются в отрезок 2 . Для волн с большей длиной волны, соответственно, имеем обратную зависимость – с увеличением длины волны меньшее число волн укладывается в отрезок 2 .

Также, возрастание волнового числа от частоты следует дисперсионного уравнения:

То есть, возрастание значение волнового числа приводит к возрастанию частоты колебаний.

3. Крутизна дисперсионной характеристики увеличивается с возрастанием толщины пленки.

Для рассмотрения данного явления запишем дисперсионное уравнение для симметричных волн:

Зафиксируем значение частоты и увеличим значение толщины пленки. При увеличении толщины пленки L уменьшается поперечное волновое число , поскольку при фиксированной частоте значение магнитной проницаемости также остается неизменным, как и значение тангенса. Следовательно, при уменьшении поперечного волнового числа уменьшается и продольное волновое число . Отсюда следует, что дисперсионная характеристика с увеличением толщины пленки становится круче, то есть нарастание происходит значительно быстрее.