Лабы Гагарин / Лаба 1

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ФЭТ

отчет

по лабораторной работе №1

по дисциплине «Физические основы электронно-ионной технологии»

Тема: Исследование физики процесса упругого столкновения двух частиц

Студенты гр. 0207 _________________ Маликов Б.И.

_________________ Горбунова А.Н.

Преподаватель _________________ Гагарин А.Г.

Санкт-Петербург

2023

ЦЕЛЬ РАБОТЫ

Исследование физики процесса столкновения двух частиц.

ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

1) Построение зависимости коэффициента изменения энергии от углов рассеяния при нецентральном столкновении для разных масс первой частицы (код программы представлен в приложении). Выражения для нахождения коэффициента изменения энергии представлены ниже (1), (2).

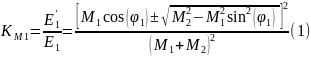
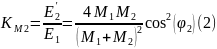
Построение зависимости K_M1 от угла рассеяния при разных M₁ для случая, когда в формуле стоит «+».

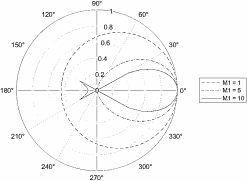
Рисунок 1 – Зависимость K_M1 от угла рассеяния при разных массах, когда в формуле стоит «+»

Построение зависимости K_M1 от угла рассеяния при разных M₁ для случая, когда в формуле стоит «-».

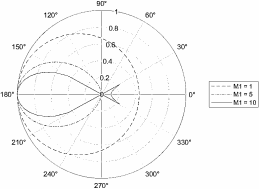
Рисунок 2 - Зависимость K_M1 от угла рассеяния при разных массах, когда в формуле стоит «-»

Построение зависимости K_M2 от угла рассеяния при разных M₁.

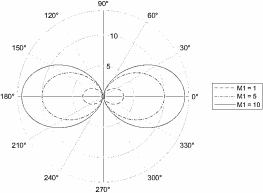
Рисунок 3 - Зависимость K_M1 от угла рассеяния при разных массах

2) Построение зависимости коэффициента изменения энергии от углов рассеяния при нецентральном столкновении для разных масс первой частицы (код программы представлен в приложении) с учетом относительного угла Θ. Использованы те же выражения для нахождения коэффициента изменения энергии, но углы рассеяния рассчитаны по формулам (3), (4).

Построение зависимости K_M1 от угла рассеяния при разных M₁ для случая, когда в формуле стоит «+».

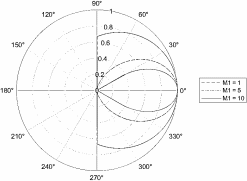
Рисунок 4 – Зависимость K_M1 от угла рассеяния при разных массах, когда в формуле стоит «+»

Построение зависимости K_M1 от угла рассеяния при разных M₁ для случая, когда в формуле стоит «-».

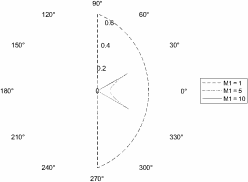
Рисунок 2 - Зависимость K_M1 от угла рассеяния при разных массах, когда в формуле стоит «-»

Построение зависимости K_M2 от угла рассеяния при разных M₁.

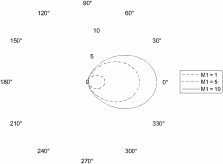
Рисунок 3 - Зависимость K_M1 от угла рассеяния при разных массах

ВЫВОД

В ходе данной лабораторной работы были построены зависимости коэффициентов изменения энергии K_M1 и K_M2 от углов рассеяния при различных массах налетающей частицы.

ПРИЛОЖЕНИЕ

Код программы для построения зависимости коэффициентов изменения энергии от углов рассеяния для нецентрального удара

clear

clc

close all

M1 = [1,5,10];

M2 = 5;

psi1 = linspace(0,2*pi,101);

psi12 = linspace(0,2*pi,101);

i = 1;

k = 1;

while i<=3

while k<102

if abs(sin(psi1(k)))<(M2/M1(i))

Km1(i,k)=Km1plus(M1(i),M2,psi1(k));

Km1_minus(i,k)=Km1minus(M1(i),M2,psi1(k));

else

Km1(i,k)=0;

end

Km2(i,k)=Km2fu(M1(i),M2,psi2(k));

k=k+1;

end

k=1;

i=i+1;

end

k=1;

while k<102

Km1_1(k)=Km1(1,k);

Km1_2(k)=Km1(2,k);

Km1_3(k)=Km1(3,k);

Km1_1_minus(k)=Km1_minus(1,k);

Km1_2_minus(k)=Km1_minus(2,k);

Km1_3_minus(k)=Km1_minus(3,k);

Km2_1(k)=Km2(1,k);

Km2_2(k)=Km2(2,k);

Km2_3(k)=Km2(3,k);

k=k+1;

end

polarplot(psi1,Km1_1,'--')

hold on

polarplot(psi1,Km1_2, '-.')

hold on

polarplot(psi1,Km1_3)

legend('M1 = 1', 'M1 = 5', 'M1 = 10')

figure

polarplot(psi1,Km1_1_minus, '--')

hold on

polarplot(psi1,Km1_2_minus, '-.')

hold on

polarplot(psi1,Km1_3_minus)

legend('M1 = 1', 'M1 = 5', 'M1 = 10')

figure

polarplot(psi2,Km2_1, '--')

hold on

polarplot(psi2,Km2_2, '-.')

hold on

polarplot(psi2,Km2_3)

legend('M1 = 1', 'M1 = 5', 'M1 = 10')

function y=Km1plus(M1,M2,psi1)

y=((M1*cos(psi1)+sqrt(M2^2-(M1^2)*sin(psi1)^2))^2)/(M1+M2)^2;

end

function y=Km1minus(M1,M2,psi1)

y=((M1*cos(psi1)-sqrt(M2^2-(M1^2)*sin(psi1)^2))^2)/(M1+M2)^2;

end

function y=Km2fu(M1,M2,psi2)

y=((4*M1*M2)/(M1+M2))*cos(psi2)^2;

end

Код программы для построения зависимости коэффициентов изменения энергии от углов рассеяния для нецентрального удара с учетом относительного угла

clear

clc

close all

teta = linspace(0,2*pi,1010);

M1 = [1,5,10];

M2 = 5;

i = 1;

k = 1;

while i<=3

while k<1011

psi1(i,k)=atan(sin(teta(k))/(cos(teta(k)+(M1(i)/M2))));

psi2(k)=(pi/2)-(teta(k)/2);

if abs(sin(psi1(i,k)))<(M2/M1(i))

Km1(i,k)=Km1plus(M1(i),M2,psi1(i,k));

Km1_minus(i,k)=Km1minus(M1(i),M2,psi1(i,k));

else

Km1(i,k)=0;

end

Km2(i,k)=Km2fu(M1(i),M2,psi2(k));

k=k+1;

end

k=1;

i=i+1;

end

k=1;

while k<1011

psi1_1(k)=psi1(1,k);

psi1_2(k)=psi1(2,k);

psi1_3(k)=psi1(3,k);

Km1_1(k)=Km1(1,k);

Km1_2(k)=Km1(2,k);

Km1_3(k)=Km1(3,k);

Km1_1_minus(k)=Km1_minus(1,k);

Km1_2_minus(k)=Km1_minus(2,k);

Km1_3_minus(k)=Km1_minus(3,k);

Km2_1(k)=Km2(1,k);

Km2_2(k)=Km2(2,k);

Km2_3(k)=Km2(3,k);

k=k+1;

end

figure

polarplot(psi1_1,Km1_1, '--')

hold on

polarplot(psi1_2,Km1_2, '-.')

hold on

polarplot(psi1_3,Km1_3)

legend('M1 = 1', 'M1 = 5', 'M1 = 10')

figure

polarplot(psi1_1,Km1_1_minus, '--')

hold on

polarplot(psi1_2,Km1_2_minus, '-.')

hold on

polarplot(psi1_3,Km1_3_minus)

legend('M1 = 1', 'M1 = 5', 'M1 = 10')

figure

polarplot(psi2,Km2_1, '--')

hold on

polarplot(psi2,Km2_2,'-.')

hold on

polarplot(psi2,Km2_3)

legend('M1 = 1', 'M1 = 5', 'M1 = 10')

function y=Km1plus(M1,M2,psi1)

y=((M1*cos(psi1)+sqrt(M2^2-(M1^2)*sin(psi1)^2))^2)/(M1+M2)^2;

end

function y=Km1minus(M1,M2,psi1)

y=((M1*cos(psi1)-sqrt(M2^2-(M1^2)*sin(psi1)^2))^2)/(M1+M2)^2;

end

function y=Km2fu(M1,M2,psi2)

y=((4*M1*M2)/(M1+M2))*cos(psi2)^2;

end