Лабы Гагарин / Лаба 3

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ФЭТ

отчет

по лабораторной работе №3

по дисциплине «Физические основы электронно-ионной технологии»

Тема: Исследование вероятности рассеяния частиц

Студенты гр. 0207 _________________ Маликов Б.И.

_________________ Горбунова А.Н.

Преподаватель _________________ Гагарин А.Г.

Санкт-Петербург

2023

ЦЕЛЬ РАБОТЫ

Целью данной лабораторной работы является исследование и сравнение двух методов расчета вероятности рассеяния частиц.

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Рассеяние – изменение траектории частицы в результате взаимодействия с другой частицей.

Налетающий пучок

Представим, что частица сталкивается с другой частицей (атомом кристаллической решетки). В результате частица рассеивается на угол θ (радианы) и некоторый телесный угол рассеяния Ω, измеряемой в стерадианах (СР).

Рассеянные частицы

Нерассеянные частицы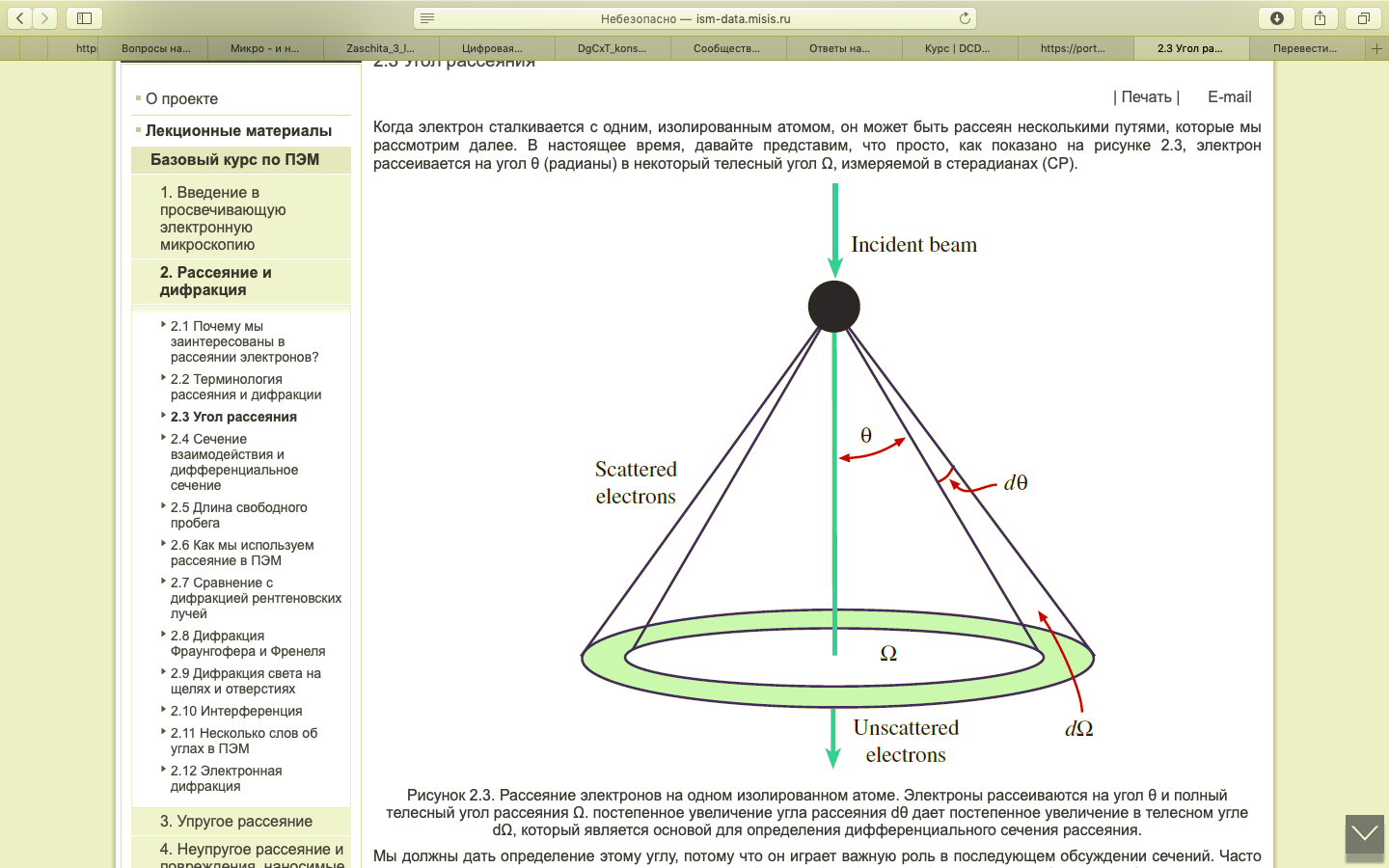

Рис. 1 – Физика процесса рассеяния частиц

Тогда, вероятность того, что рассеяния произойдет на конкретный угол рассеяния, можно записать как:

P = N_S (1)

где N_S – число центров рассеян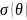ия, – сечение рассеяния, 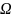– телесный угол.

ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

Основной расчет производится по следующей формуле расчета вероятности рассеяния:

P = (2)

Листинг кода:

clear

close all

e = 1.6*10^(-19);

k = 9*10^9;

E1 = 1*10^6;

Z1 = 2;

Z2 = 79;

ro = 19.3;

M2 = 197;

Na = 6.02*10^23;

Nv = ((ro*Na)/M2)*10^(-6);

V = 1/Nv;

l = sqrt(V);

Nl = 1/l;

b = -l/2 + l*rand;

d = k*((Z1*Z2*e)/E1);

tetha = 2*atan(d/(2*b));

omega = 0.5;

Ns = (Nv)^(2/3);

tetha2 = -pi:0.01:pi;

sigma_tetha = (k.*((Z1.*Z2.*e)./4./E1)).^2.*(1./sin(tetha2./2).^4);

diam = 2.*sqrt(sigma_tetha./3.14);

P = diam.*Nl.*0.5;

for i = 1:10^6

b(i) = -l/2 + l*rand;

tetha(i) = 2*atan(d/(2*b(i)));

end

figure

histogram(tetha,7,'Normalization','probability')

set(gca,'YScale','log')

hold on

plot(tetha2,P)

set(gca,'YScale','log')

figure

polarhistogram(tetha,7,'Normalization','probability')

Построение гистограмм:

P, у.е.

Рис. 1 – Гистограмма вероятности рассеяния

P, у.е.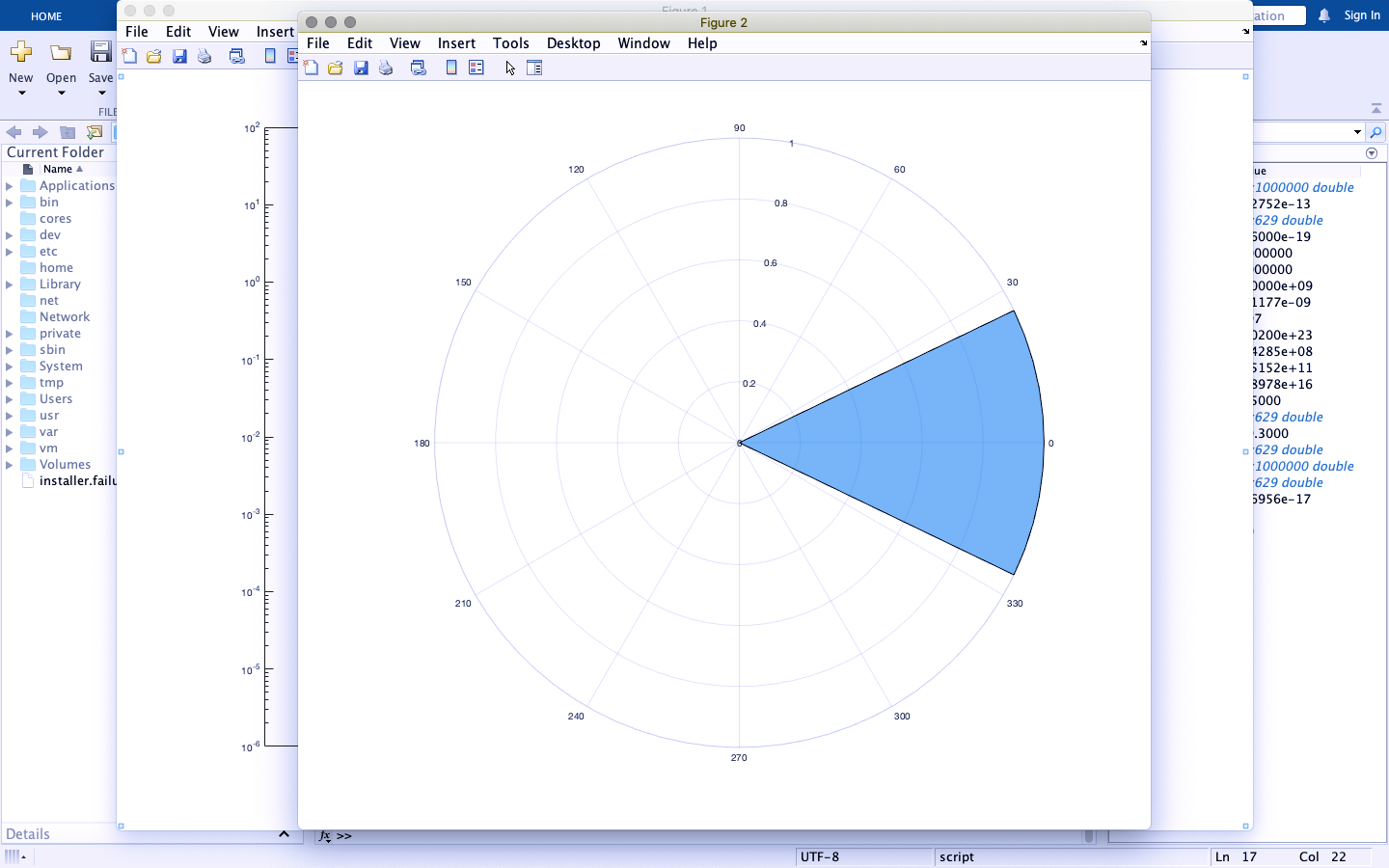

Рис. 2 – Гистограмма вероятности рассеяния в полярной системе координат

ВЫВОД

В ходе выполнения данной лабораторной работы была исследована вероятность рассеяния частиц.

Было проведено сравнения вероятности рассеяния частиц, рассчитанного одним способом, с вероятностью по формуле Резерфорда, и показано полное совпадения вероятности рассеяния, расчитанного двумя разными путями.