Методы / Учебное пособие на практику

При отсутствии внешнего источника тока стационарному состоянию перехода соответствует одинаковое положение уровней (квазиуровней) Ферми в полупроводниках. ЭД перехода в этом состоянии представлена на рис. 3.23, а. На рис.3.23, б, в, г показаны распределения ρ(x), Е(х), φ(x) в пределах перехода. Для определенности принято, что концентрация акцепторов в GaAs (NA1)

вдвое превосходит концентрацию доноров (ND1) в Al0,3Ga0,7As . Различие в

значениях , образующих гетеропереход полупроводников, обусловливает разрыв на границе их раздела напряженности электрического поля. При этом в отсутствие поверхностного заряда на границе раздела индукция электрического поля изменяется непрерывно. Контактная разность потенциалов φc, обеспечивающая выравнивание уровней Ферми в обеих частях гетероперехода, определяется разностью работ выхода А1 - А2 (рис. 3.23, г). Соотношение между разностями потенциалов границы раздела и электронейтральных областей полупроводников имеет следующий вид

тронов n различны (рис. 3.23, а). Из анализа ЭД гетероперехода следует, чтоp n , p n EC EV 0,5 эВ, т. е. различие в высоте барьеров для дырок и электронов определяется различием в значениях ширины запрещенных зон контактирующих полупроводников.

Задача 3.26. Определите численные значения C , Wn , Wp , Wp n , n

p , n p и удельную емкость Cs для гетероперехода, рассмотренного в за-

даче 3.25, при ND1 1018 см-3 и ND2 1017 см-3

Дополнительные сведения и пояснения. Для получения расчетных формул следует воспользоваться результатами решения задачи 3.12 и учесть различие

и EG в гетероструктуре. В частности, ширина области обеднения для р-обла-

сти перехода будет определяться уравнением

а удельная емкость гетероперехода

42

Задача 3.27. Проанализируйте с помощью ЭД процессы переноса носителей заряда в р–п-гетеропереходе при наличии разности потенциалов U, создаваемой внешним источником.

Решение. Порядок решения аналогичен использованному в задаче 3.15. Анализ проводится на основе представлений о влиянии внешней разности потенциалов на интенсивности дрейфовых и диффузионных потоков основных н неосновных носителей заряда через гетеропереход. Как и в случае гомоперехода (см. рис. 3.14), при U = 0 эти потоки скомпенсированы и ток через переход отсутствует.

При прямой полярности U высота энергетических барьеров для основных носителей уменьшается на значение eU, что приводит к экспоненциальному увеличению их диффузионных потоков. В отличие от гомоперехода, в

рассматриваемом случае p n (см.

рис. 3.23, а) и приращения Jn,D и

J p,D не одинаковы, т. е. Jn,D J p,D

(см. рис. 3.24, а). Одновременно с уменьшением высоты барьера происходит сужение области, обедненной

носителями заряда W, и возрастание удельной емкости Cs гетероперехода.

Соответствующие значения W и Cs могут быть получены из соотноше-

ний (3.14) и (3.15) путем замены в них c на c U .

Неосновные носители заряда, инжектируемые в приконтактные области перехода, создают в них избыточную концентрацию неосновных носителей,

E

причем концентрация избыточных электронов в e kT раз больше, чем дырок

(ΔE – разность энергетических барьеров). Эта особенность гетеропереходов определяет их преимущество перед гомопереходами – способность создавать высокий уровень инжекции носителей одного знака (суперинжекция). Распределения концентраций неосновных носителей показаны на рис. 3.24, б.

43

При обратной полярности U процессы переноса носителей заряда анало-

гичны описанным в задаче 3.15, а значения W и Cs определяются уравнениями

(3.14) и (3.15) путем замены c на c U .

Для получения ВАХ гетероперехода необходимо учитывать большое число различных явлений, оказывающих влияние на механизм проводимости [2]. В общем виде ВАХ гетеропереходов может быть аппроксимирована зави-

eU

симостью вида I I0(e kT 1), где I0 – обратный ток, который не стремится к насыщению, а подчиняется степенной зависимости I0 ~ |U|m, (0,5 ≤ m ≤ 4).

Задача 3.28. Построить ЭД селективно легированного (ND1 >> ND2) гетероперехода GaAs – AlxGa1 xAs , нахо-

дящегося в состоянии термодинамического равновесия. Исходные параметры контактирующих материалов иллюстрируются ЭД на рис. 3.25.

Дополнительные сведения и пояс-

нения. Селективно легированный ге- Рис. 3.25. Энергетические диаграммы GaAs теропереход - это переход, в котором

AlxGa1 xAs ) сильно легирован, а узкозонный (GaAs ) – высокой степени чи-

стоты и структурного совершенства. В настоящее время гетеропереходы ис-

пользуются для создания нового типа полевых транзисторов – транзисторов со сверхвысокой подвижностью электронов в канале. В основе создания та-

кого транзистора лежит идея пространственного разделения легирующих примесных центров от носителей тока с помощью гетероперехода.

гетическая диаграмма, соответствующая этому случаю, показана на рис. 3.26.

44

Особенностью ЭД является наличие в переходной области гетероперехода в

GaAs, тонкого слоя, аккумулирующего захваченные из AlxGa1 xAs элек-

троны. Так как эти электроны находятся в очень чистом (нелегированном) арсениде галлия, их подвижность исключительно высока, особенно при низких температурах. Тонкий аккумулирующий слой в поперечном сечении представляет собой узкую (порядка длины волны Де Бройля) потенциальную яму, которая тем уже, чем выше концентрация стекающих туда электронов. Движение электронов в таком слое носит двухмерный характер - свободное вдоль канала, поперек его оно ограничено потенциальными барьерами. При двухмерном характере движения электронов их подвижность возрастает.

3.4. Структура металл – диэлектрик – полупроводник

Трехкомпонентная структура металл – диэлектрик – полупроводник (МДП) занимает одно из важнейших мест в полупроводниковой электронике, поскольку её свойства определяют характеристики важнейших элементов ИС, таких как полевой транзистор с изолированным затвором (МДП-транзи- стор) и МДП-конденсаторы. Структура, в которой в качестве диэлектрика используется собственный оксид, называется МОП-структурой. Во всем дальнейшем анализе рассматриваются свойства идеализированной МОП-струк- туры, т. е. структуры, в которой границы раздела между материалами плоские и не содержат зарядов.

Как и ранее, исходной позицией для анализа свойств МОП-структуры является построение ее энергетической диаграммы. Чтобы построить ЭД МОП-структуры, воспользуемся основными принципами и идеями, которые были применены при изучении структур металл – полупроводник и р–n-пере- ходов. Исходная позиция для анализа состоит в том, что такие системы при тепловом равновесии характеризуются постоянным уровнем Ферми.

Задача 3.29. Изобразите ЭД равновесной МОП-структуры: алюминийоксид кремния – кремний р-типа при следующих значениях параметров:

AM = 4,1 эВ; 0 = 0,95 эВ;EG = 8 эВ; s = 4,05 эВ; As = 4,9 эВ; EG,s = 1,12 эВ.

Решение. Изобразим ЭД для металла, диэлектрика и полупроводника,

когда указанные тела не находятся в непосредственном контакте (рис. 3.27).

Работа выхода металла AM меньше работы выхода полупроводника As . По-

этому при образовании плотного контакта между элементами структуры,

электроны из металла будут переходить в полупроводник. Через диэлектрик

45

перенос заряда невозможен, так как в идеальном случае в нем нет подвижных носителей зарода. Однако практически в любой МОП-структуре ИС всегда имеется какая-либо цепь для передачи заряда, которая обладает на много большей проводимостью по сравне-

нию с оксидом. В результате перехода части электронов из металла в полу-

проводник на поверхности металла образуется тонкий слой положитель-

ного заряда, а в приповерхностной об-

ласти полупроводника – слой из отри-

цательного заряда акцепторных ионов, образовавшийся вследствие ухода части дырок (приход электро-

нов из металла в полупроводник экви-

валентен уходу части дырок из ва-

лентной зоны). На диэлектрике обра-

зуется падение потенциала, обуслов-

ленное накопленным с обеих его сторон зарядом. Поскольку в диэлектрике нет свободных зарядов, дебаевский радиус экранирования оказывается намного больше толщины диэлектрика и распределение потенциала в нем близко к линейному. В приповерхностной области полупроводника образу-

ется изгиб зон, который рассчитывается путем решения уравнения Пуассона для обедненной области [3]. Таким образом, перераспределение зарядов между металлом и полупроводником приводит к выравниванию уровней

Ферми и образованию контактной разности потенциалов c As AM , ко- e

торая распределяется между диэлектриком и обедненной областью полупро-

водника. В рассматриваемом случае падение напряжения на оксиде состав-

ляет 0,4 В. Точное значение разности энергий между металлом и полупро-

водником будет определено при решении задачи 3.30. Равновесная энергети-

ческая диаграмма МОП-структуры показана на рис. 3.28. Из энергетической диаграммы следует, что в равновесных условиях при заданных параметрах контактирующих материалов в приповерхностной области полупроводника образуется слой, обедненный основными носителями заряда.

46

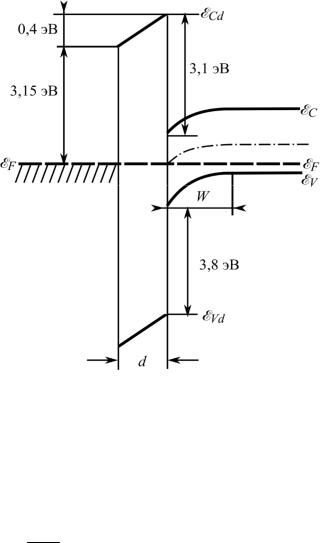
Задача 3.30. Определите толщину слоя оксида кремния в МОП-струк- туре, энергетическая диаграмма которой изображена на рис. 3.28. Параметры структуры соответствуют указанным в задаче 3.29.

женности электрического поля в обедненном слое Es необходимо восполь-

зоваться соотношениями (3.4) и (3.5), находя концентрацию акцепторной примеси из уравнения

Ei -Ef

NA p nie kT

Задача 3.31. Изобразите ЭД МОП-структуры, рассмотренной в задаче 3.29, если к металлу подключен отрицательный полюс внешнего источника

U0 0,8 В.

Задача 3.32. Изобразите ЭД МОП-структуры при наличии разности потен-

циалов U0 , создаваемой внешним источником.

Дополнительные сведения и пояснения.

1. Анализ влияния смещающего напряжения на ЭД проведем, пренебрегая контактной разностью потенциалов по сравнению с искривлением зон, обу-

47

словленным внешним смещением. Такое пренебрежение эквивалентно усло-

вию равенства работ выхода ( AM Ai As ) соответствует «плоским зонам»,

2. Поскольку через МОП-струк- туру постоянный ток протекать не может, такое состояние на ЭД характери-

зуется условием dEs 0, т. е. уровень

наклон или искривление как в p–n-переходе.

Решение. Если к металлу приложен отрицательный полюс внешнего источника, а к полупроводнику – положительный, то уровень Ферми в полупроводнике опустится на величину eU0 (рис. 3.30, а), при этом часть этого напряжения падает на изоляторе, а часть на полупроводнике, приводя к искривлению энергетических зон. В этом случае у поверхности кремния скапливается дополнительное количество дырок, т. е. формируется обогащенный слой. Приповерхностный обогащенный слой представляет собой слой положительного объемного заряда, образованного свободными носителями. Толщина этого слоя W определяется длиной Дебая и имеет значение порядка десятков нанометров, т.е. соизмерима с толщиной диэлектрика. Энергетическая диаграмма и распределение зарядов в МОП-структуре показаны на рис. 3.30, а, б.

Если к металлу приложен положительный полюс, а к полупроводнику – отрицательный, то уровень Ферми в полупроводнике поднимается на значение eU0 (рис. 3.31, а). В этом случае из приповерхностной области полупроводника будут уходить дырки, и будет возрастать отрицательный заряд нескомпенсированных акцепторных ионов. Соответственно будет расти и положительный заряд на поверхности металла. Такая ситуация называется режимом обеднения.

48

50