Лабы / 1 Лаба / DgCXT_Labs_0207_Маликов_1

ЦЕЛЬ РАБОТЫ

Целью работы является ознакомление с программой MAX+PLUS и

исследование таблиц истинности ряда логических элементов (ЛЭ).

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

Логические элементы используются для построения, в том числе,

комбинаторных узлов, как в интегральном исполнении (в виде интегральных микросхем) так и в виде обычных схем. Комбинаторные узлы – схемы,

имеющие некоторое количество входов и выходов, и при этом состояния выходов определяются мгновенно и исключительно текущим состоянием входов (то есть комбинаторные схемы не имеют свойства запоминать и хранить данные). Существует большое количество типовых комбинаторных узлов – дешифраторы и шифраторы, демультиплексоры и мультиплексоры,

сумматоры, компараторы и т.д. Как правило, такие узлы имеют группы входов, логические уровни которых интерпретируются как двоичные числа.

Разрядность чисел соответствует числу входов, объединенных в группу.

Компараторы служат для сравнения групп логических сигналов (чисел).

Компараторы имеют два многоразрядных входа A[n..0] и B[n..0] и выходы: AB (при этом разрядность входных чисел составляет n+1). Уровень лог. «1» на одном из выходов показывает, как соотносятся числа A и B. Схемы компараторов могут иметь входы для каскадирования, т.е. увеличения разрядности всей схемы за счет соединения в цепочки нескольких микросхем или схем меньшей разрядности.

Сумматоры служат, как следует из названия, для сложения чисел.

Многоразрядный сумматор, в том числе, в интегральном исполнении, состоит из цепочки одноразрядных сумматоров – несложных схем, которые способны складывать одноразрядные числа. Алгоритм работы сумматора не сложнее алгоритма сложения чисел «в столбик». Для младшего бита в каскаде

2

справедливо: 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, 1 + 1 = 0 с переносом в старший разряд. Следующие по старшинству одноразрядные сумматоры в каскаде имеют вход переноса и реализуют таблицу истинности, показанную на Рис. 13, а. Здесь: Ai, Bi – i-тые биты операндов сложения A и B, Ci – вход переноса i-того сумматора, Ci+1 – выход переноса i-того сумматора в старший разряд

(подключается ко входу переноса следующего по старшинству одноразрядного сумматора). Одноразрядный сумматор, не имеющий входа переноса – полусумматор.

ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

1. Исследование таблицы истинности ЛЭ типа 2И-НЕ

Рис. 1 – Схема для исследования таблицы истинности ЛЭ типа 2И-НЕ

Таблица 1. Таблица истинности ЛЭ типа 2И-НЕ

3

2. Исследование таблицы истинности ЛЭ типа 2ИЛИ-НЕ

Рис. 2 – Схема для исследования таблицы истинности ЛЭ типа 2ИЛИ-НЕ

Таблица 2. Таблица истинности ЛЭ типа 2ИЛИ-НЕ

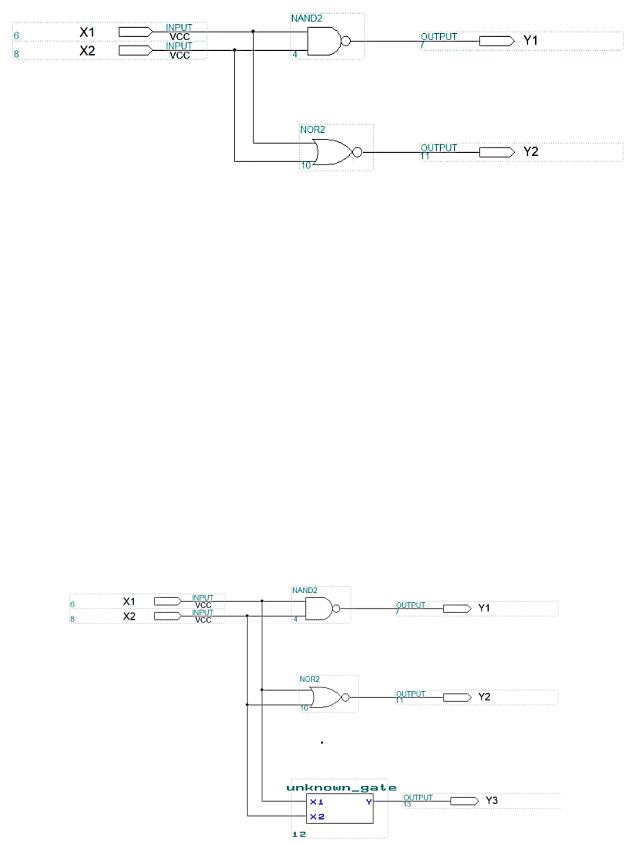
3. Исследование неизвестного ЛЭ

Рис. 3 – Схема для исследования таблицы истинности неизвестного ЛЭ

4

Таблица 3. Таблица истинности неизвестного ЛЭ

Таким образом, анализируя таблицу истинности для неизвестного ЛЭ,

делаем вывод, что неизвестный ЛЭ – ИСКЛЮЧАЮЩЕЕ ИЛИ.

4. Исследование схемы реализации функции ИЛИ на ЛЭ типа 2И-НЕ

Рис. 4 - Схема реализации функции ИЛИ на ЛЭ типа 2И-НЕ

Таблица 4. Таблица истинности функции ИЛИ на ЛЭ типа 2И-НЕ

5

5. Исследование схемы реализации функции И на ЛЭ типа 2ИЛИ-НЕ

Рис. 5 - Схема реализации функции И на ЛЭ типа 2ИЛИ-НЕ

Таблица 5. Таблица истинности функции И на ЛЭ типа 2ИЛИ-НЕ

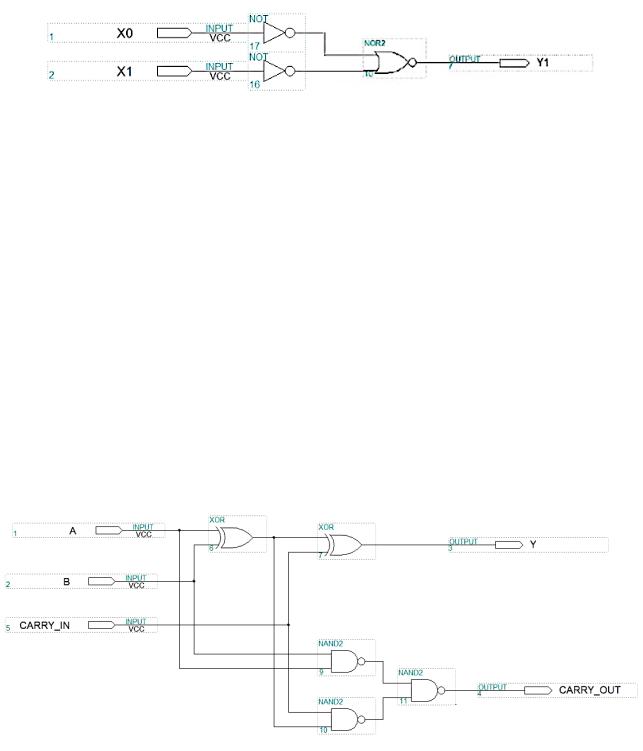
6. Исследование схемы одноразрядного сумматора

Рис. 6 – Схема одноразрядного сумматора

6

7. Исследование схемы дешифратора «2 в 4»

Рис. 7 – Схема дешифратора «2 в 4»

Таблица 7. Таблица истинности дешифратора «2 в 4»

ВЫВОД

В ходе выполнения данной работы были изучены основные инструменты и элементы MAX+PLUS. Проанализированы операции дизъюнкции и конъюнкции на примере ЛЭ типа ИЛИ и ЛЭ типа И. Также,

изучен инвертор (логический НЕ).

Сравнивая таблицу истинности функции ИЛИ на ЛЭ типа 2И-НЕ

(таблица 4) и таблица истинности функции И на ЛЭ типа 2ИЛИ-НЕ (таблица

5), делаем вывод, что обе таблицы являются полной противоположностью друг другу.

Были исследованы схемы одноразрядного сумматора (таблица 6) и

дешифратора (таблица 7), изучены принципы их работы.

8