Лабы Дроздовский / 2 Лаба / ЛР_2_ГорбуноваМаликовЩубрет_0207

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ФЭТ

отчет

по лабораторной работе №2

по дисциплине «Микроволновая техника и измерения»

Тема: Измерение характеристик коаксиального кабеля с помощью

панорамного измерителя КСВ и затуханий

Студенты гр. 0207 _________________ Маликов Б.И.

_________________ Горбунова А.Н.

_________________ Щубрет С.Л.

Преподаватель _________________ Дроздовский А.В.

Санкт-Петербург

2023

ЦЕЛЬ РАБОТЫ

Изучение характеристик коаксиального кабеля и приобретение практических навыков использования векторного анализатора цепей.

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

Блок-схема установок для измерения параметров коаксиального кабеля «на проход» и «на отражение» показаны на рис. 1, а, б, соответственно. В состав установки входят следующие основные элементы: 1 – векторный анализатор цепей; 2 – управляющий компьютер; 3 – исследуемый коаксиальный кабель; 4 – коаксиальный тройник; 5 – аттенюатор (согласованная нагрузка).

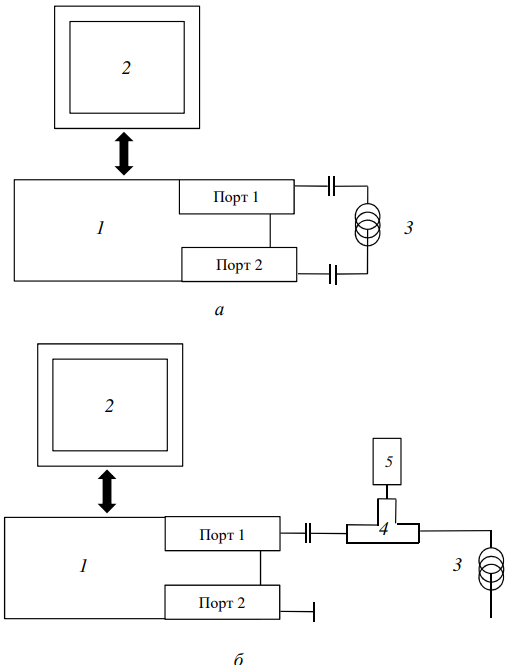
Рисунок 1

Рассмотрим эквивалентную схему тройника с подключенными аттенюатором и кабелем. При этом длиной тройника и затуханием в коаксиальном кабеле пренебрежем. В случае, если напряжение падающей волны в сечении тройника x = 0 то есть (рис. 2 и рис. 3), то напряжение падающей волны на конце отрезка коаксиальной линии длиной l будет составлять , где β – постоянная распространения волны в коаксиальном кабеле. Так как в рассматриваемом случае на конце коаксиальной линии осуществляется режим холостого хода, то там наблюдается максимальное значение полного напряжения и ноль полного тока.

С другой стороны, от разомкнутого конца линии должна отражаться полностью вся мощность, падающая на него. Отсюда можно сделать вывод, что модуль комплексного коэффициента отражения равен единице (иначе бы отражалась не вся мощность), а фаза коэффициента отражения ϕ = 0 (т. е. отражение волны напряжения происходит без изменения знака, и наблюдается максимум напряжения на конце линии). Таким образом, .

Рисунок 2

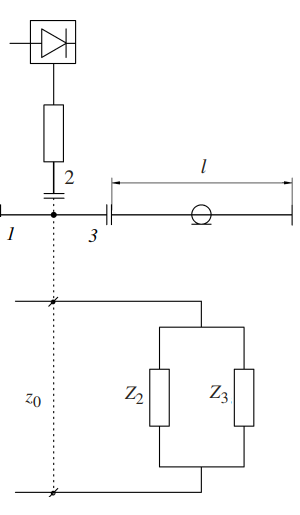
Рисунок 3

Отраженная волна напряжения распространяется от конца линии навстречу падающей волне. Зная токи напряжения в каждой точке линии передачи можно определить входное сопротивление отрезка коаксиальной линии как

Таким образом, можно представить рассматриваемый тройник с включенными в его плечи отрезком коаксиального кабеля и согласованной нагрузкой в виде параллельного соединения двух сосредоточенных сопротивлений (рис. 4), т. е. со стороны плеча 1, которое имеет волновое сопротивление Z0 , будет наблюдаться параллельное включение двух входных сопротивлений плечей 2 и 3. Входное сопротивление плеча 2 – Z₂ = Z₀, так как оно нагружено на согласованную нагрузку (аттенюатор и детектор) и поглощает всю мощность, падающую на нее, а входное сопротивление плеча 3 (коаксиальный кабель) Z₃ = Z_вх. Тогда входное сопротивление всего тройника можно определить обычной формулой для параллельного соединения сопротивлений:

Одно из параллельно включенных сопротивлений является частотно-независимым (Z₂), а второе (Z₃) зависит от постоянной распространения (волнового числа) в коаксиальной линии β = 2π/λ, где λ – длина волны в линии, являющаяся частотно-зависимой: , где ε_r – диэлектрическая проницаемость диэлектрика кабеля. Соответственно, частотно-зависимым оказывается и коэффициент отражения от тройника со стороны плеча 1:

а его модуль, измеряемый в работе:

Модуль коэффициента отражения при изменении частоты (волнового числа) будет принимать максимальные и минимальные значения:

Качественная картина изменения модуля коэффициента отражения от частоты приведена на рис. 4.

При наличии затухания в кабеле коэффициент отражения в max меньше 1, а в min больше 0. Измеряя коэффициент отражения в max и min можно определить затухание кабеля:

Изменение волнового числа, соответствующее переходу из одного минимума в другой:

Выражение (6) позволяет определить одну из неизвестных характеристик кабеля − ε_r или l:

Выберем изменение волнового числа между двумя соседними минимумами 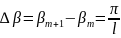и получим следующее соотношение:

ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

1. Построение передаточной характеристики, фазо-частотной характеристики и группового времени задержки коэффициента передачи с использованием короткого кабеля для КЗ.

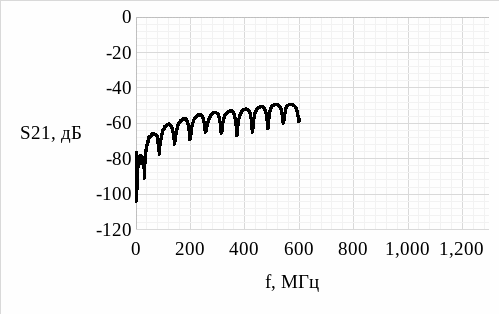
Рисунок 4 – Передаточная характеристика для короткого кабеля (КЗ)

Рисунок 5 – Фазо-частотная характеристика для короткого кабеля (КЗ)

Рисунок 6 – Зависимость группового времени задержки от частоты для короткого кабеля (КЗ)

2. Построение передаточной характеристики, фазо-частотной характеристики и группового времени задержки коэффициента передачи с использованием короткого кабеля в схеме (рис.1 б)

Рисунок 7 – Передаточная характеристика для короткого кабеля

Рисунок 8 – Фазо-частотная характеристика для короткого кабеля

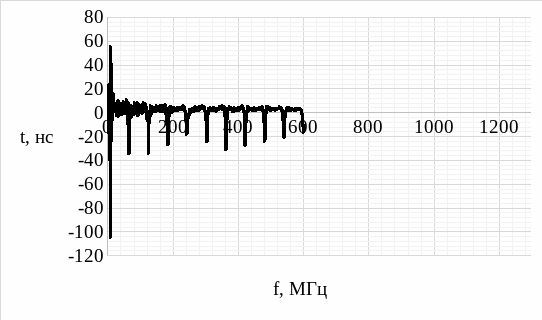
Рисунок 9 – Зависимость группового времени задержки от частоты для короткого кабеля

3. Построение передаточной характеристики, фазо-частотной характеристики и группового времени задержки коэффициента передачи с использованием длинного кабеля для КЗ.

Рисунок 10 – Передаточная характеристика для длинного кабеля (КЗ)

Рисунок 11 – Фазо-частотная характеристика для длинного кабеля (КЗ)

Рисунок 12 – Зависимость группового времени задержки от частоты для длинного кабеля (КЗ)

Рисунок 13 – Передаточная характеристика для длинного кабеля

Рисунок 14 – Фазо-частотная характеристика для длинного кабеля

Рисунок 15 – Зависимость группового времени задержки от частоты для длинного кабеля

4. Расчет средней диэлектрической проницаемости диэлектрика первого кабеля по результатам измерений 5 минимумов, учитывая, что длина первого кабеля l₁ = 75 см с использованием формулы (8).

Для f_m+1 = 63.12 МГц и f_m = 2.47 МГц:

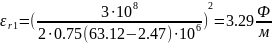
Для f_m+1 = 305.73 МГц и f_m = 182.26 МГц:

Для f_m+1 = 552.67 МГц и f_m = 429.2 МГц:

Для f_m+1 = 801.78 МГц и f_m = 678.31 МГц:

Для f_m+1 = 1048.72 МГц и f_m = 925.25 МГц:

Определение средней диэлектрической проницаемости:

5. Определение длины второго кабеля с использованием диэлектрической проницаемости, рассчитанной в п.4 по формуле (7).

6. Расчет времени группового запаздывания для первого и второго кабеля с использованием формулы (9).

Расчет времени группового запаздывания для первого кабеля.

Для f_m+1 = 63.12 МГц и f_m = 2.47 МГц:

Для f_m+1 = 305.73 МГц и f_m = 182.26 МГц:

Для f_m+1 = 552.67 МГц и f_m = 429.2 МГц:

Для f_m+1 = 801.78 МГц и f_m = 678.31 МГц:

Для f_m+1 = 1048.72 МГц и f_m = 925.25 МГц:

Расчет времени группового запаздывания для второго кабеля.

Для f_m+1 = 26.294 МГц и f_m = 6.799 МГц:

Для f_m+1 = 65.285 МГц и f_m = 45.789 МГц:

Для f_m+1 = 102.109 МГц и f_m = 82.614 МГц:

Для f_m+1 = 138.935 МГц и f_m = 119.439 МГц:

Для f_m+1 = 175.796 МГц и f_m = 156.264 МГц:

ВЫВОД

В ходе данной лабораторной работы были построены передаточные характеристики, фазо-частотные характеристики и групповое время задержки для длинного и короткого кабеля согласно схемам, представленным на рис.1.

При увеличении длины кабеля максимумы передаточной характеристики сближаются (рис.13), Фазо-частотная характеристика на тех же частотах достигает меньших значений.

Также была рассчитана диэлектрическая проницаемость ε_r = 2.292 Ф/м. Определено время группового запаздывания на основании передаточных характеристик для короткого и длинного кабеля. У длинного кабеля время группового запаздывания больше, что доказывают как расчеты, так и построенные характеристики.