Лабы Дроздовский / 1 Лаба / ЛР_1_ГорбуноваМаликовЩубрет_0207

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ФЭТ

отчет

по лабораторной работе №1

по дисциплине «Микроволновая техника и измерения»

Тема: Определение полного сопротивления элементов СВЧ-

тракта с помощью измерительной линии

Студенты гр. 0207 _________________ Маликов Б.И.

_________________ Горбунова А.Н.

_________________ Щубрет С.Л.

Преподаватель _________________ Дроздовский А.В.

Санкт-Петербург

2023

ЦЕЛЬ РАБОТЫ

Определение полного сопротивления элементов СВЧ-тракта и освоение практических приемов работы с измерительной линии и круговой диаграммой полных сопротивлений.

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

Измерения коэффициента отражения и полного сопротивления узлов или элементов СВЧ-трактов необходимы при решении задач согласования, а также при определении параметров эквивалентных схем и частотных характеристик устройств СВЧ. Измерения с помощью измерительной линии (ИЛ) являются простыми, достаточно точными и не требуют сложного измерительного оборудования при экспериментальном определении коэффициента отражения и полного сопротивления.

Принцип измерения основан на известной зависимости между сопротивлением исследуемого элемента и распределением напряженности электрического поля волны вдоль однородной линии передачи, соединяющей измеряемый элемент с генератором. Если сопротивление элемента Z_н равно волновому сопротивлению линии z₀, то в ней устанавливается режим бегущей волны (отсутствуют отраженные волны). В случае, если Z_н ≠ z₀, в передающей линии устанавливается режим стоячих волн, получающихся как суперпозиция падающих и отраженных волн. Коэффициент отражения определяется отношением напряженности электрического поля отраженной волны E0 к напряженности падающей волны E_п в месте расположения элемента, т. е. Г_Н = Е₀/Е_п.

В общем виде коэффициент отражения является комплексным числом: 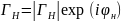, где Γ_н – модуль отношения напряжений; φ_н – фазовый сдвиг между падающей и отраженной волнами на исследуемом объекте. Комплексный коэффициент отражения связан с полным сопротивлением 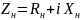соотношением:

Сопротивление нагрузки СВЧ-тракта обычно выражают в нормированных на волновое сопротивление подводящей линии значениях:

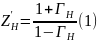
На практике, как правило, измеряют коэффициент стоячей волны напряжения (КСВ), определяемый отношением максимального значения напряжения стоячей волны в линии к его минимальному значению: , и положение ближайшего от нагрузки минимума напряжения в линии z_min. Через эти параметры можно легко определить модуль и фазу коэффициента отражения:

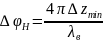
где λ_В – длина волны в линии, которая определяется как удвоенное расстояние между ближайшими минимумами.

Так как калибровка сопротивления нагрузки измерительной линии производится по короткому замыканию, то , т. е. 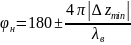, где ∆z_min – расстояние между минимумом Z_{min кз} в режиме короткого замыкания (калибровки) и минимумом Z_min в режиме подключенной нагрузки Z_н. При этом знак «–» используется, если минимум Z_min расположен между Z_{min кз} и нагрузкой, и «+», если минимум Z_min от нагрузки лежит в сторону генератора от Z_{min кз}.

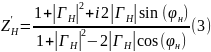
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ

Структурная схема экспериментальной установки представлена на рис. 1. В состав установки входят следующие элементы: 1 – измерительный СВЧ-генератор; 2 – частотомер; 3 – регулируемый аттенюатор; 4 – измерительная линия; 5 – индикатор; 6 – исследуемый элемент; 7 – согласованная нагрузка.

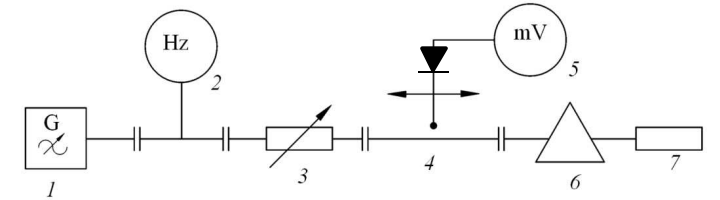
Рисунок 1

Для исследования режимов бегущей и стоячей волн вместо элементов 6 и 7 помещаются эталонная нагрузка или короткозамыкатель соответственно.

ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

1. Построение графиков распределения напряженности электрического поля вдоль линии при подключении согласованной нагрузки, короткозамыкателя и исследуемых элементов.

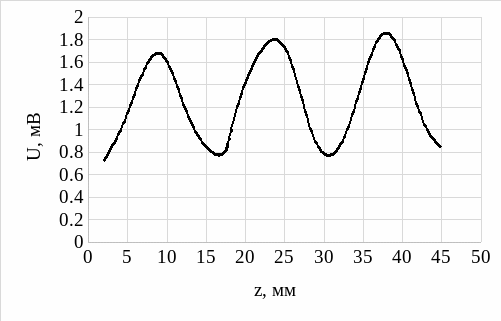
Рисунок 2 – Распределение поля вдоль линии без нагрузки

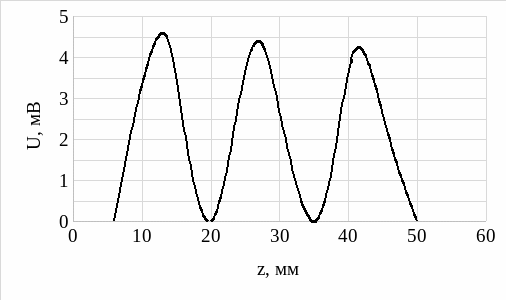
Рисунок 3 – Распределение поля вдоль линии при коротком замыкании

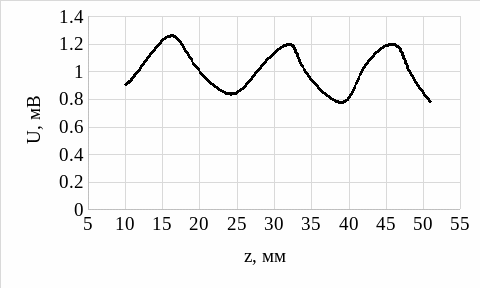
Рисунок 4 – Распределение поля вдоль линии при подключении к нагрузке с широкой щелью

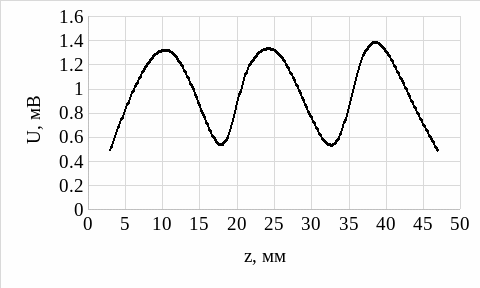
Рисунок 5 – Распределение поля вдоль линии при подключении к нагрузке с узкой щелью

Рисунок 6 – Распределение поля вдоль линии при включении ферритового вентиля (прямое)

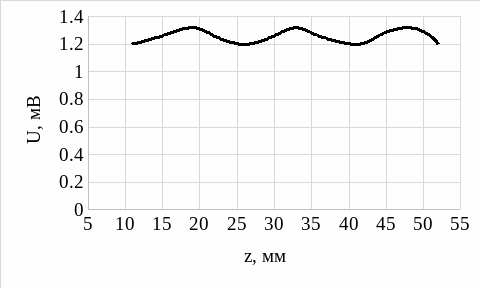
Рисунок 7 – Распределение поля вдоль линии при включении ферритового вентиля (обратное)

2. Определение теоретической длины волны по формуле (4) и сравнение ее с экспериментальными значениями.

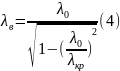
Расчет теоретической длины волны (λ₀ = с/f, λ_кр = 2а, f = 13.63 ГГц):

Определение экспериментальных длин волн с использованием рис.2 – рис.7:

Без нагрузки: λ_в = 3 см

Короткое замыкание: λ_в = 2,8 см

Широкая щель: λ_в = 2,8 см

Узкая щель: λ_в = 3 см

Ферритовый вентиль (прямое включение): λ_в = 2,8 см

Ферритовый вентиль (обратное включение): λ_в = 3 см

3. Определение КСВ по формуле (5) для каждого вида нагрузки.

Без нагрузки: ρ = 1.528

Короткое замыкание: -

Широкая щель: ρ = 1.183

Узкая щель: ρ = 1.658

Ферритовый вентиль (прямое включение): ρ = 1.173

Ферритовый вентиль (обратное включение): ρ = 1.05

4. Определение расстояния между минимумом короткого замыкания и минимумом в режиме согласованной нагрузки. (6 мм)

Без нагрузки: Δz = 4 мм

Широкая щель: Δz = -4 мм

Узкая щель: Δz = 3 мм

Ферритовый вентиль (прямое включение): Δz = 1 мм

Ферритовый вентиль (обратное включение): Δz = -5 мм

5. Определение фазы коэффициента отражения с использованием формулы (6).

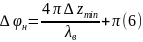
Без нагрузки: Δϕ_н = 4.817 рад.

Широкая щель: Δϕ_н = 1.346 рад.

Узкая щель: Δϕ_н = 4.398 рад.

Ферритовый вентиль (прямое включение): Δϕ_н = 3.59 рад.

Ферритовый вентиль (обратное включение): Δϕ_н = 1.047 рад.

6. Определение модуля коэффициента отражения с использованием формулы (2).

Без нагрузки: 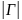= 0.209

Широкая щель: = 0.084

Узкая щель: = 0.248

Ферритовый вентиль (прямое включение): = 0.079

Ферритовый вентиль (обратное включение): = 0.024

7. Определение полного сопротивления исследуемых элементов с использованием формулы (3).

Без нагрузки: Z_н = 0.956 + 0.416i Ом

Широкая щель: Z_н = 1.024 + 0.169i Ом

Узкая щель: Z_н = 0.772 + 0.388i Ом

Ферритовый вентиль (прямое включение): Z_н = 0.865 + 0.06i Ом

Ферритовый вентиль (обратное включение): Z_н = 1.023 + 0.043i Ом

8. Построение зависимостей АЧХ и ФЧХ для трех видов нагрузок (1, 7 и 9 схемы, изображенные на рис.8).

Рисунок 8

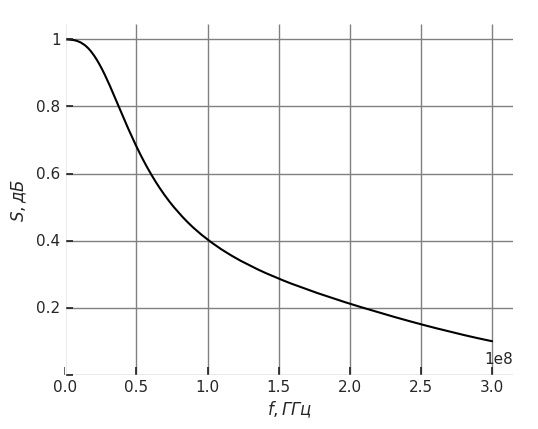
Рисунок 9 – АЧХ для первого типа нагрузки

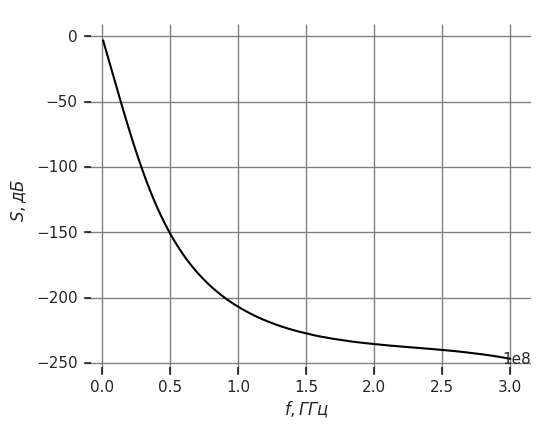
Рисунок 10 – ФЧХ для первого типа нагрузки

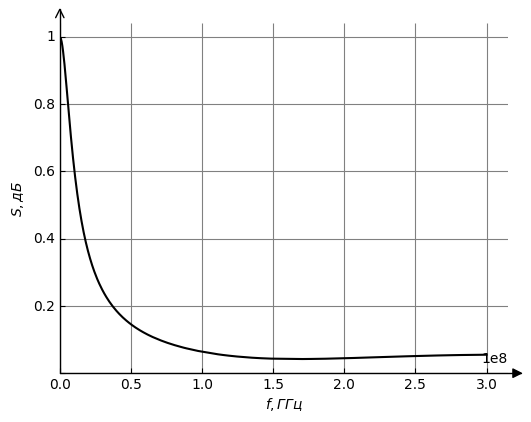
Рисунок 11 – АЧХ для второго типа нагрузки

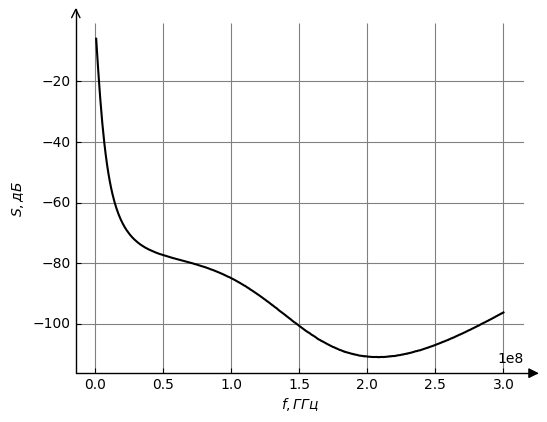
Рисунок 12 – ФЧХ для второго типа нагрузки

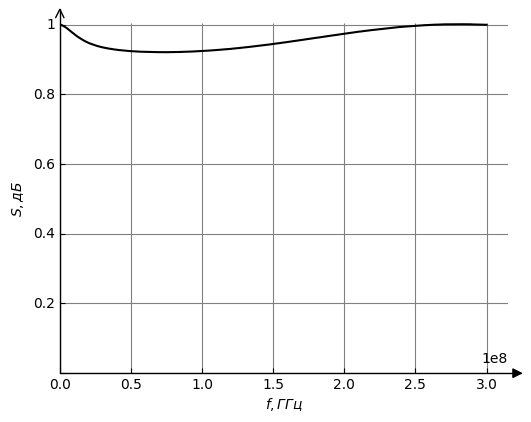
Рисунок 13 – АЧХ для третьего типа нагрузки

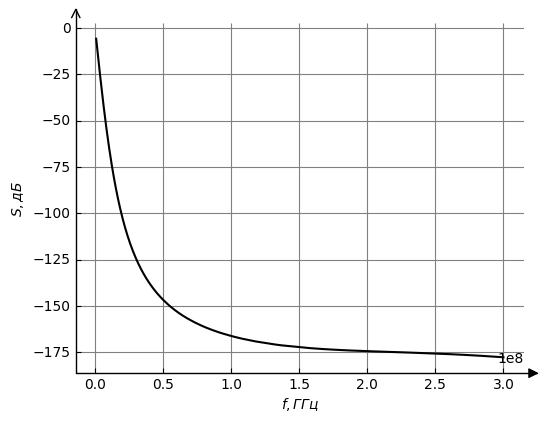
Рисунок 14 – ФЧХ для третьего типа нагрузки

9. Построение диаграмм Вольперта-Смита для различных типов нагрузки.

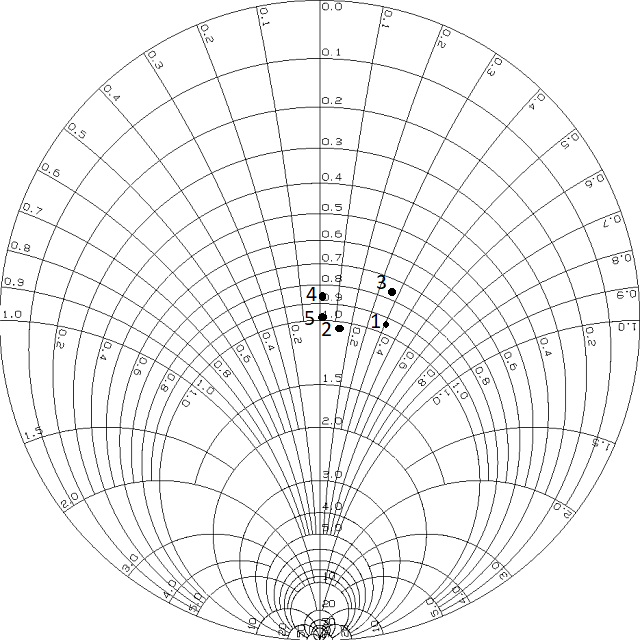
Рисунок 15 – Диаграмма Вольперта-Смита (1 – без нагрузки, 2 – широкая щель, 3 – узкая щель, 4 – ферритовый вентиль (прямой), 5 – ферритовый вентиль (обратный))

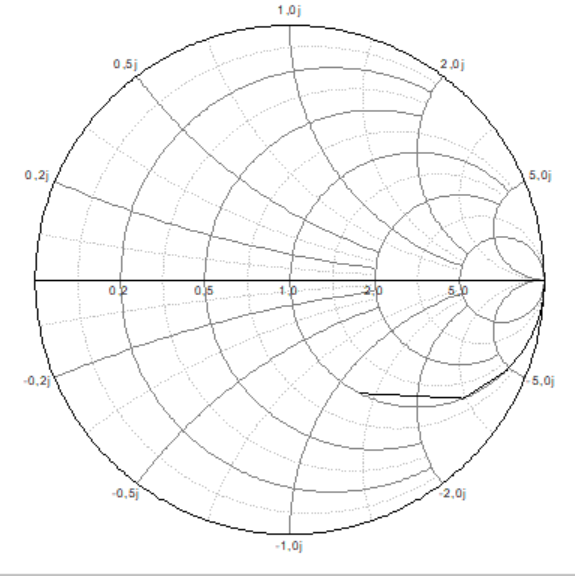
Рисунок 16 – Диаграмма Вольперта-Смита для первого типа нагрузки

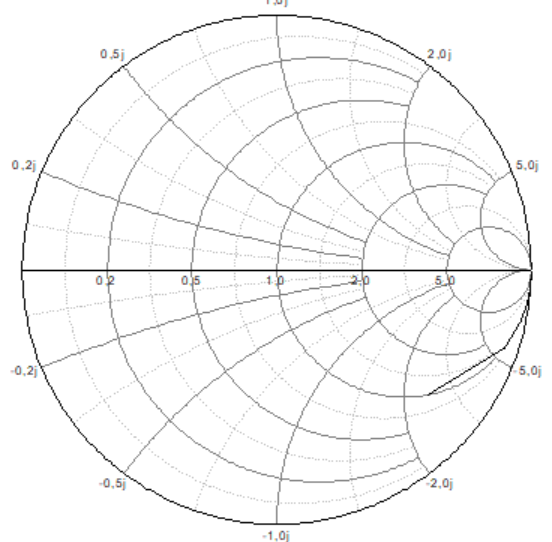
Рисунок 17 – Диаграмма Вольперта-Смита для второго типа нагрузки

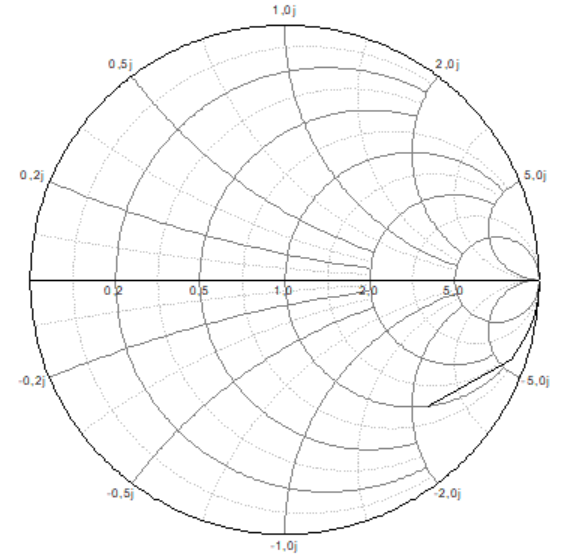
Рисунок 18 – Диаграмма Вольперта-Смита для третьего типа нагрузки

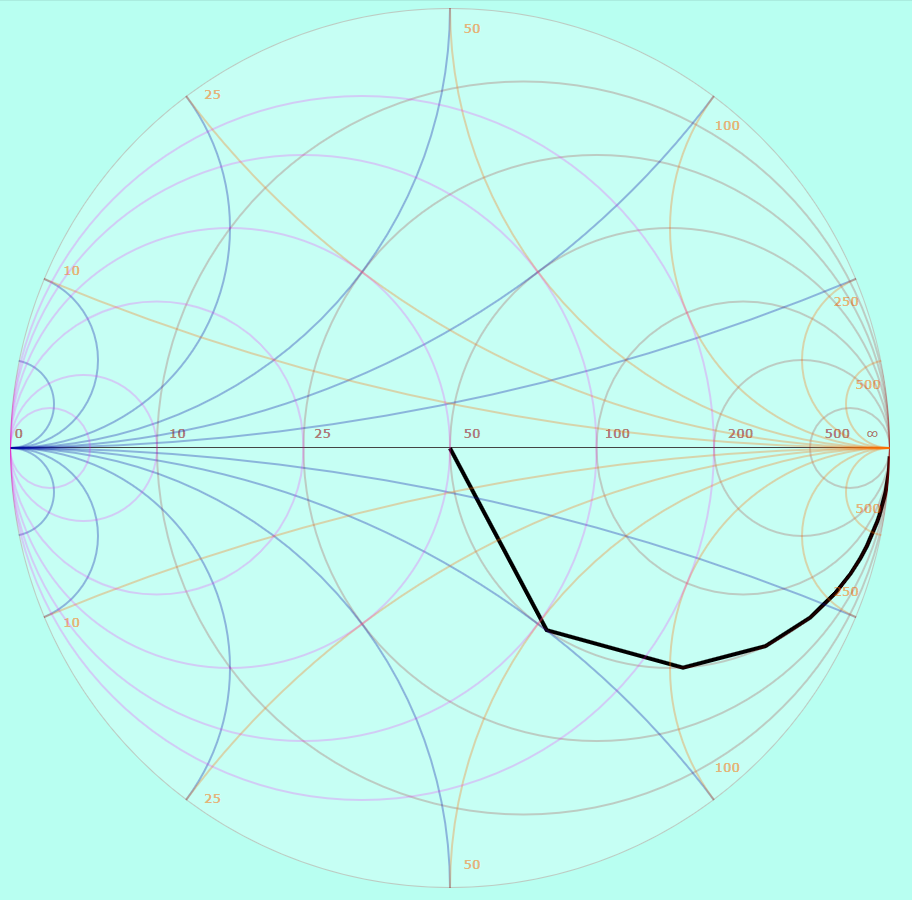
Рисунок 19 – Диаграмма Вольперта-Смита для второго типа нагрузки

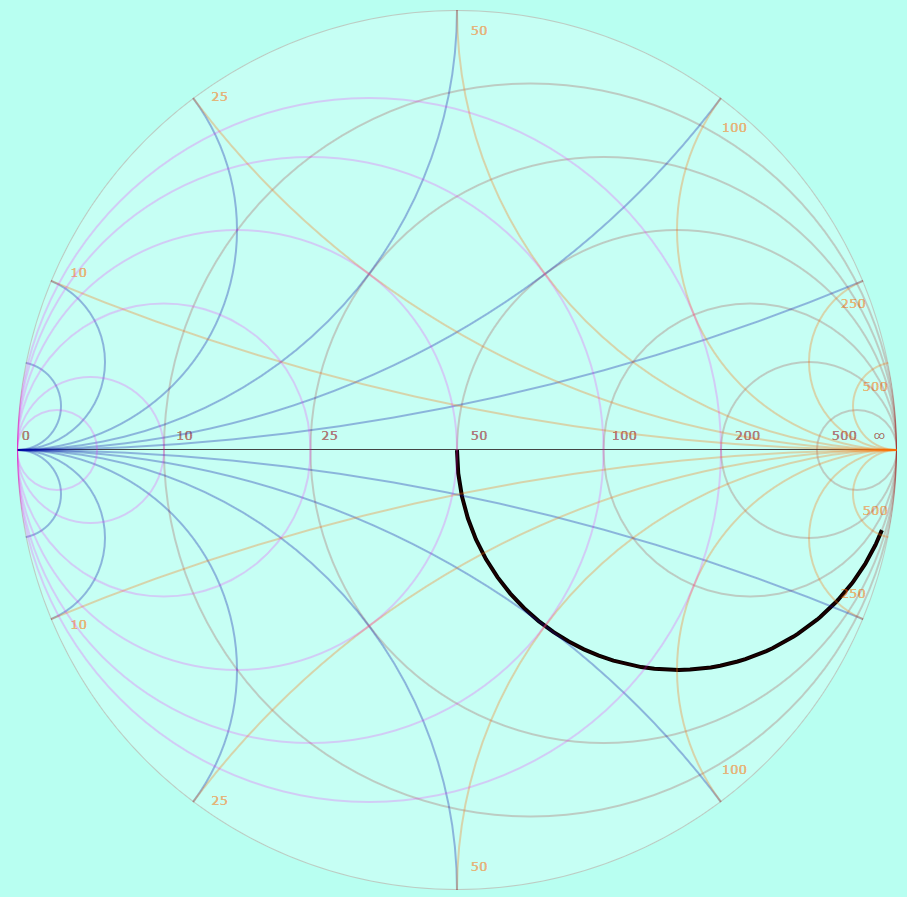
Рисунок 20 – Диаграмма Вольперта-Смита для третьего типа нагрузки

ВЫВОД

В ходе данной лабораторной работы определили полное сопротивление элементов СВЧ-тракта и освоили практические приемы работы с измерительной линией и круговой диаграммой полных сопротивлений. Также были рассчитаны коэффициент отражения, коэффициент стоячей волны и фаза, на основании которых рассчитано значение полного сопротивления.

На основании рис.2 – рис.7 можно сделать вывод, что наибольший максимум наблюдается при КЗ, остальные же все значительно ниже.

Также в работе были построены АЧХ, ФЧХ и диаграммы Вольперта-Смита для трех типов нагрузки.

18