Добавил:

MalikovB Адепт твердотельной электроники, последователь учений Михайлова Н.И. Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный электротехнический университет "ЛЭТИ"

Предмет:

Микроволновая техника измерения

Файл:

Метода / Метода на лабы

.pdf

Скачиваний:

Добавлен:

21.06.2024

Размер:

447.33 Кб

Скачать

☆

1 / 41 2 3 4 > Следующая >>>

МИНОБРНАУКИ РОССИИ

––––––––––––––––––––––––––––––––––––––––––––––––––––

Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В. И. Ульянова (Ленина)

–––––––––––––––––––––––––––––––––––––––––––

А. В. ДРОЗДОВСКИЙ Н. Г. КОВШИКОВ

МИКРОВОЛНОВАЯ ТЕХНИКА И ИЗМЕРЕНИЯ

Учебно-методическое пособие

Санкт-Петербург Издательство СПбГЭТУ «ЛЭТИ»

2018

УДК 615.849.112(07) ББК З 840.4я7

Д 75

Дроздовский А. В., Ковшиков Н. Г.

Д 75 Микроволновая техника и измерения: учеб.-метод. пособие. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2018. 32 с.

ISBN 978-5-7629-2195-4

Приводится описание лабораторных работ по дисциплинам «Микровол- новая техника и измерения» и «СВЧ-техника и измерения». Содержит краткие описания некоторых приборов СВЧ, методов и схем измерения их СВЧ-харак- теристик, задания для лабораторных работ и порядок их выполнения. Сфор- мулированы контрольные вопросы для самостоятельной подготовки.

Предназначено для студентов, обучающихся по направлению 11.03.04 – «Электроника и наноэлектроника».

УДК 615.849.112(07) ББК З 840.4я7

Рецензент доцент кафедры криогенной техники университета ИТМО, канд. техн. наук. О. В. Пахомов.

Утверждено редакционно-издательским советом университета

в качестве учебно-методического пособия

ISBN 978-5-7629-2195-4

– фазовый

Лабораторная работа № 1 ОПРЕДЕЛЕНИЕ ПОЛНОГО СОПРОТИВЛЕНИЯ ЭЛЕМЕНТОВ

СВЧ-ТРАКТА С ПОМОЩЬЮ ИЗМЕРИТЕЛЬНОЙ ЛИНИИ

Цель работы: определение полного сопротивления элементов СВЧ-тракта и освоение практических приемов работы с измерительной линией и круговой диаграммой полных сопротивлений.

1.1. Основные положения

Измерения коэффициента отражения и полного сопротивления узлов или элементов СВЧ-трактов необходимы при решении задач согласования, а также при определении параметров эквивалентных схем и частотных характеристик устройств СВЧ. Измерения с помощью измерительной линии (ИЛ) являются простыми, достаточно точными и не требуют сложного измерительного обо- рудования при экспериментальном определении коэффициента отражения и полного сопротивления.

Принцип измерения основан на известной зависимости между сопротив- лением исследуемого элемента и распределением напряженности электриче- ского поля волны вдоль однородной линии передачи, соединяющей измеряе- мый элемент с генератором. Если сопротивление элемента Zн равно волно- вому сопротивлению линии Z0 , то в ней устанавливается режим бегущей волны (отсутствуют отраженные волны). В случае, если Zн ≠ Z0 , в передаю- щей линии устанавливается режим стоячих волн, получающихся как суперпо- зиция падающих и отраженных волн. Коэффициент отражения определяется отношением напряженности электрического поля отраженной волны E0 к напряженности падающей волны Eп в месте расположения элемента, т. е.

Γн = E0 / Eп .

В общем виде коэффициент отражения является комплексным числом: Γн = Γн exp(Iφн) , где Γн – модуль отношения напряжений; φн

сдвиг между падающей и отраженной волнами на исследуемом объекте. Ком- плексный коэффициент отражения связан с полным сопротивлением Zн = Rн + IX н соотношением

Γн = (Zн − Z0 )/ (Zн + Z0 ).

Сопротивление нагрузки СВЧ-тракта обычно выражают в нормирован-

ных на волновое сопротивление подводящей линии значениях:
Zн ' = Zн / Z0 = (1 + Γн ) / (1 − Γн ) .	(1.1)

На практике, как правило, измеряют коэффициент стоячей волны напря- жения (КСВ), определяемый отношением максимального значения напряже- ния стоячей волны в линии к его минимальному значению: ρ = U max /U min , и положение ближайшего от нагрузки минимума напряжения в линии zmin . Че- рез эти параметры можно легко определить модуль и фазу коэффициента от- ражения:

	Γн	= (ρ – 1)/ (ρ+1);	(1.2)

∆φн = 4π∆Zmin / λв ,

где λв – длина волны в линии, которая определяется как удвоенное расстояние между ближайшими минимумами.

Так как калибровка сопротивления нагрузки измерительной линии произ- водится по короткому замыканию, то φн = φк ± ∆φн, т. е.

φн =180 ± 4π ∆Zmin / λв , где ∆zmin – расстояние между минимумом Zmin кз в режиме короткого замыкания (калибровки) и минимумом Zmin в режиме под- ключенной нагрузки Zн . При этом знак «–» используется, если минимум Zmin расположен между Zmin кз и нагрузкой, и «+», если минимум Zmin от нагрузки лежит в сторону генератора от Zmin кз .

С учетом (1.1) и (1.2), можно определить полное сопротивление исследу- емого элемента:

' = R '+ IX ' = 1 −

exp(Iφ

) / 1 −

exp(Iφ

) =

(1.3)

Γн

+ I2

Γн

− 2

Γн

sin(φн)

/ 1 +

cos(φн) .

Полное сопротивление удобно находить с помощью круговых диаграмм полных сопротивлений, где все вышеуказанные параметры ( ρ, Zmin , Γн ) свя- заны с сеткой активных и реактивных составляющих сопротивления.

1.2. Описание экспериментальной установки

Структурная схема экспериментальной установки представлена на рис. 1.1. В состав установки входят следующие элементы: 1 – измерительный

СВЧ-генератор; 2 – частотомер; 3 – регулируемый аттенюатор; 4 – измеритель- ная линия; 5 – индикатор; 6 – исследуемый элемент; 7 – согласованная нагрузка.

Рис. 1.1

Для исследования режимов бегущей и стоячей волн вместо элементов 6

и7 помещаются эталонная нагрузка или короткозамыкатель соответственно.

1.3.Задание и порядок выполнения работы

1.Ознакомиться с аппаратурой, входящей в экспериментальную уста-

новку.

2.Изучить конструкцию и основные характеристики измерительной ли- нии (ИЛ), методику градуировки.

3.Изучить круговую диаграмму полных сопротивлений и методику опре- деления с ее помощью полного сопротивления и проводимости.

4.Включить измерительный генератор согласно инструкции и настроить его на заданную преподавателем частоту Fи.

5.Настроить измерительную линию на заданную частоту. Для этого со- брать схему (рис. 1.1), заменив в ней исследуемый элемент на короткозамыка- тель. От генератора подать в линию высокочастотный сигнал и с помощью ру- чек настройки диодной и зондовой резонансной камер ИЛ получить максимум на шкале индикаторного прибора. При этом глубину погружения зонда сле- дует устанавливать минимальной с учетом реальной чувствительности инди- катора. Уровень мощности в ИЛ следует поддерживать таким, чтобы показа- ния индикатора соответствовали полной шкале при установке зонда в макси- мум напряженности электрического поля.

6.Измерить распределение напряженности электрического поля вдоль линии при подключенном короткозамыкателе и при замене его на согласован- ную нагрузку. Определить длину волны в линии и сравнить с расчетной [см.

(1.3)].

7. Провести измерения, необходимые для определения полного сопротивле- ния. Для этого зафиксировать положение Z1 одного из минимумов напряжен- ности поля при подключенном короткозамыкателе. Затем собрать схему со- гласно рис. 1.1 и определить положение минимума Z2 , ближайшего по коор- динате к ранее найденному Z1 со стороны нагрузки. Относительный фазовый

сдвиг определяется соотношением 4π∆Zmin / λв = 4π(Z2 − Z1 ) / λв . Для опреде- ления КСВ необходимо: установить зонд в положение минимума и зафикси-

ровать показания индикатора и показания аттенюатора A ; затем, установив

зонд в положение максимума, увеличить затухание аттенюатора A2 до полу- чения прежних показаний индикатора (U1) и определить разность в децибелах

по шкале аттенюатора: A	− A = ∆A . Значение КСВ в децибелах определяется
2	1
∆A , а с учетом	того, что ∆A=20 lg (	Emax	/	Emin	), получим
∆A , а с учетом	того, что ∆A=20 lg (	Emax	/	Emin	), получим

ρ = Emax / Emin =10∆A/20 . При использовании амплитудного детектора ха- рактеристика которого близка к квадратичной, значение КСВ можно найти так: КСВ = Umax / U min , где Umax и Umin – показания индикатора в макси- мумах и минимумах стоячей волны.

8.Повторить пп. 4−7 на других частотах (по указанию преподавателя).

9.Определить полное сопротивление и проводимость исследованного

элемента, используя круговую диаграмму и результаты измерений ( ρ, Zmin ,

λв ).

10. Рассчитать активные и реактивные составляющие полного сопротив- ления, используя (1.2) и (1.3).

1.4.Содержание отчета

1.Схема измерительной установки.

2.Основные технические характеристики измерительных приборов.

3.Эскиз исследуемых элементов и поперечного сечения волновода с ука- занием основных геометрических размеров.

4.Результаты расчета длины волны λв теор в волноводе на измеренной

частоте Fи сопоставленной с экспериментально полученной λв эксп.

5.Графики распределения напряженности электрического поля вдоль ли- нии при подключении согласованной нагрузки, короткозамыкателя и исследу- емых элементов. На графиках указать значение λв и КСВ.

6.Основные элементы круговой диаграммы с нанесенными на нее значе- ниями экспериментально найденных точек, определяющих Zн ' и Yн ' .

1.5.Контрольные вопросы

1.В чем отличие режима бегущих волн от режима стоячих волн, при ка- ких условиях они реализуются?

2.Почему длина волны в волноводе отличается от длины волны в свобод- ном пространстве?

3.Что такое согласование, и какими способами оно достигается?

4.На чем основан метод определения полных сопротивлений с помощью измерительной линии?

5.Каковы основные источники погрешности при определении полного сопротивления с помощью измерительной линии?

6.Как с помощью круговой диаграммы определить полное сопротивле- ние и проводимость нагрузки?

7.Что такое одномодовый режим работы волновода, и при каких усло- виях он реализуется?

Лабораторная работа № 2

ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК КОАКСИАЛЬНОГО КАБЕЛЯ С ПОМОЩЬЮ ПАНОРАМНОГО ИЗМЕРИТЕЛЯ КСВ И ЗАТУХАНИЙ

Цель работы: изучение характеристик коаксиального кабеля и приобрете- ние практических навыков использования векторного анализатора цепей.

2.1. Основные положения

Используемый в данной работе векторный анализатор цепей «Обзор TR1300/1» (далее – «анализатор цепей») производства фирмы ООО «ПЛА- НАР» предназначен для исследования передаточных характеристик радиоча- стотных цепей в частотном диапазоне от 300 кГц до 1300 МГц при значениях передаваемой мощности от –55 дБм до +26 дБм. Векторный анализатор цепей

позволяет осуществлять измерение частотных зависимостей амплитуды, фазы, коэффициента стоячей волны, вещественной и мнимой части величины сопро- тивления, группового времени задержки для прошедшего и отраженного ра- диосигналов.

2.2. Описание экспериментальной схемы

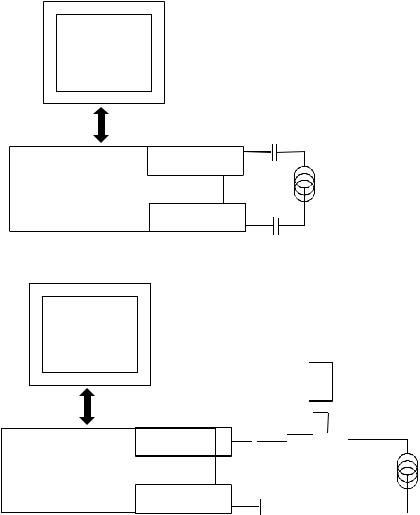
Блок-схема установок для измерения параметров коаксиального кабеля «на проход» и «на отражение» показаны на рис. 2.1, а, б, соответственно. В состав установки входят следующие основные элементы: 1 – векторный ана- лизатор цепей; 2 – управляющий компьютер; 3 – исследуемый коаксиальный кабель; 4 – коаксиальный тройник; 5 – аттенюатор (согласованная нагрузка).

Порт 1

1	3

Порт 2

			5


				4
	Порт 1
	Порт 1
		3
1
1

Порт 2

Рис. 2.1.

Рассмотрим эквивалентную схему тройника с подключенными аттенюа- тором и кабелем. При этом длиной тройника и затуханием в коаксиальном ка- беле пренебрежем. В случае, если напряжение падающей волны в сечении тройника X = 0 есть Uɺпад(0) (рис. 2.2 и рис. 2.3), то напряжение падающей

волны на конце отрезка коаксиальной линии длиной L будет составлять Uɺпад(L ) = Uɺпад(0) exp(−IβL ) , где β – постоянная распространения волны в коак-

сиальном кабеле. Так как в рассматриваемом случае на конце коаксиальной линии осуществляется режим холостого хода, то там наблюдается максималь- ное значение полного напряжения и ноль полного тока.

С другой стороны, от разомкнутого конца линии должна отражаться пол- ностью вся мощность, падающая на него. Отсюда можно сделать вывод, что модуль комплексного коэффициента отражения

Uɺ

Iɺ

βL=M

Iɺ

Uɺ

Iɺ

βL=Mπ +π/2

Iɺ

Uɺ

βL=(M + 1)π

Iɺ

Uɺ

Iɺ

Рис. 2.2	Рис. 2.3
Рис. 2.2
	9

– диэлектрическая

Γ = Γ exp(−Iφ) = Uɺотр / Uɺпад равен единице (иначе бы отражалась не вся мощ- ность), а фаза коэффициента отражения ϕ = 0 (т. е. отражение волны напряже- ния происходит без изменения знака, и наблюдается максимум напряжения на конце линии). Таким образом, Uɺотр(L ) =Uɺпад(0)exp(−IβL ) .

Отраженная волна напряжения распространяется от конца линии навстречу падающей волне. Зная токи напряжения в каждой точке линии пе- редачи можно определить входное сопротивление отрезка коаксиальной ли-

нии как
Zвх = Uɺ(0) / Iɺ(0) = −IZ0 ctg(βL ) .	(2.1)

Таким образом, можно представить рассматриваемый тройник с вклю- ченными в его плечи отрезком коаксиального кабеля и согласованной нагруз- кой в виде параллельного соединения двух сосредоточенных сопротивлений (рис. 2.4), т. е. со стороны плеча 1, которое имеет волновое сопротивление Z0 , будет наблюдаться параллельное включение двух входных сопротивлений плечей 2 и 3. Входное сопротивление плеча 2 – Z2 = Z0 , так как оно нагружено на согласованную нагрузку (аттенюатор и детектор) и поглощает всю мощ- ность, падающую на нее, а входное сопротивление плеча 3 (коаксиальный ка- бель) Z3 = Zвх (2.1). Тогда входное сопротивление всего тройника можно определить обычной формулой для параллельного соединения сопротивле- ний:

Zвх = Z2Z3 / (Z2 + Z3 ).

(2.2)

Одно из параллельно включенных сопротивлений является частотно-не- зависимым ( Z2 ), а второе ( Z3 ) зависит от постоянной распространения (вол- нового числа) в коаксиальной линии β = 2π/λ, где λ – длина волны в линии, являющаяся частотно-зависимой: λ = с / (εR F ), где εR

проницаемость диэлектрика кабеля. Соответственно, частотно-зависимым оказывается и коэффициент отражения от тройника со стороны плеча 1:

Γ = ( Z2Z3 / (Z2 + Z3 ) − Z0 )/ ( Z2Z3 / (Z2 + Z3 ) + Z0 )=
		= −1 / [1 − 2Ictg(βL )],		(2.3)
а его модуль, измеряемый в работе:
	Γ	= 1 / (1 + 4ctg2	(βL )) 1/ 2 .	(2.4)

1 / 41 2 3 4 > Следующая >>>