Лабы / Лаба 2 / ФТТ Лаба 2 Отчет

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра фотоники

отчет

по лабораторной работе №2

по дисциплине «Физика твердого тела»

Тема: Температурная зависимость электропроводности металлов

Вариант №7

Студент гр. 0207 _________________ Маликов Б.И.

Преподаватель _________________ Пухова В.М.

Санкт-Петербург

2022

ЦЕЛЬ РАБОТЫ

Целью работы является изучение температурного хода проводимости металлов в широком интервале температур с учетом различных механизмов рассеяния носителей заряда.

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

Электрическое сопротивление проводников обусловлено процессами рассеяния электронов проводимости, т. е. конечной величиной средней длины свободного пробега. Наиболее важными механизмами рассеяния носителей заряда являются, как правило, рассеяние на тепловых колебаниях кристаллической решетки (электрон-фононное рассеяние) и столкновения с дефектами решетки, в частности, с примесными атомами. В случае металла дефектный вклад в сопротивление не зависит от температуры T, в то время как электрон-фононный сложным образом растет с температурой. Обсуждение температурной зависимости электропроводности удобно проводить, используя для σ формулу Друде-Лоренца:

(1)

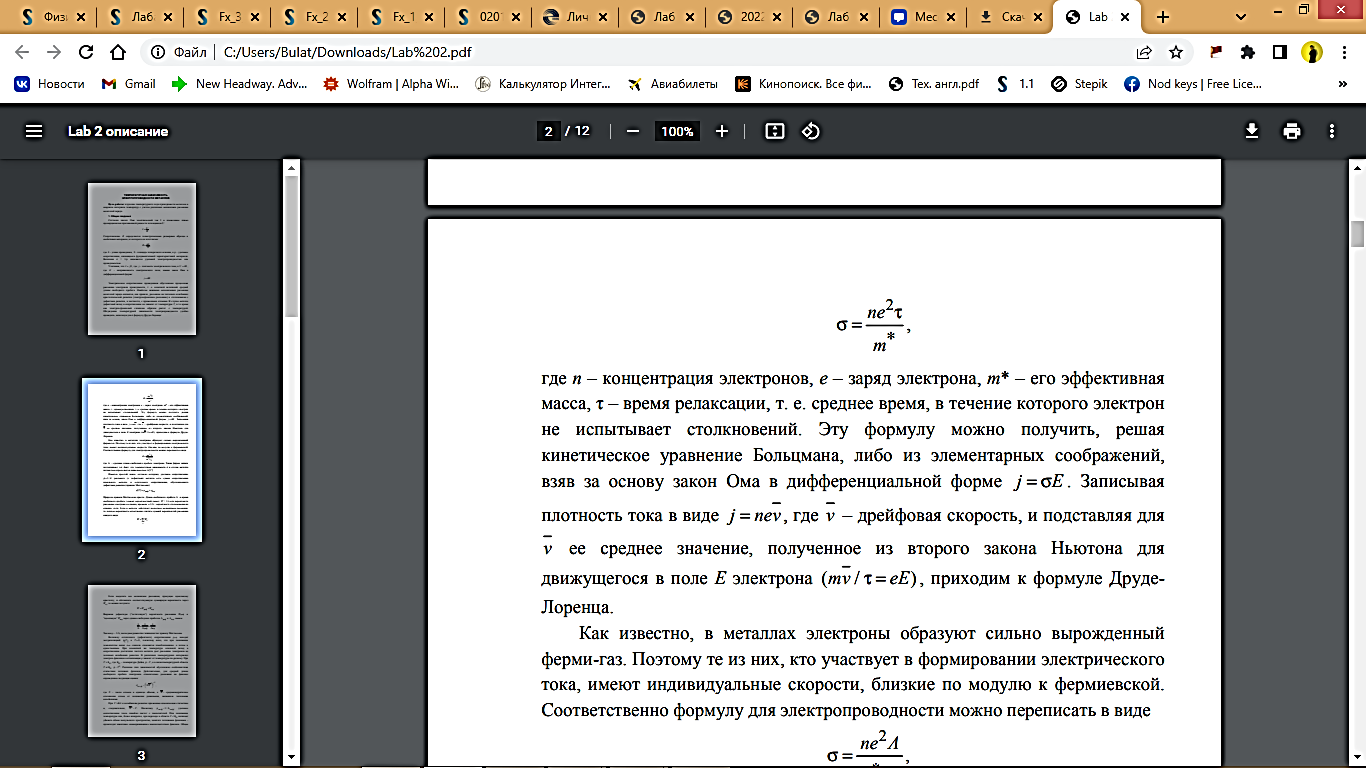
где n – концентрация электронов, e – заряд электрона, m* – его эффективная масса, τ – время релаксации, т. е. среднее время, в течение которого электрон не испытывает столкновений. Эту формулу можно получить, решая кинетическое уравнение Больцмана, либо из элементарных соображений, взяв за основу закон Ома в дифференциальной форме j = σE.

Электропроводность металлов создается свободными электронами, способными покинуть атомы, т есть валентными электронами, находящимися на энергетических уровнях валентной зоны. Электроны могут находиться на строго определенных энергетических уровнях, энергетическая плотность которых вблизи границ энергетических зон изменяется по параболическому закону:

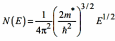(2)

Вероятность заполнения энергетических уровней электронами определяется функцией Ферми–Дирака:

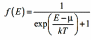
(3)

В металлических пленках длина свободного пробега электронов Λδ будет меньше, чем в объемном материале Λ . Пусть δ – толщина металлической пленки; β – доля электронов, отражающихся от поверхностей пленки зеркально. Тогда влияние размерного эффекта на длину свободного пробега металлической пленки можно вычислить по формулам:

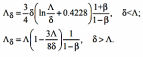
(4)

ДАННЫЕ ДЛЯ ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ

Табл. 1

Исходные данные

Металл	z	d, г/см3	A, г/моль	ρ при 273 К, мкОм·см	αp, 1/К	Температура Дебая, К
Цезий Cs	1	1,87	133	18,1	0,005	43

k = 1,38∙10^-23 [Дж/К] = 8,617∙10^-5 [эВ]

N_a = 6,02∙10²³ [моль^-1]

m = 9,1∙10^-31 [кг]

q = 1,6∙10^-19 [Кл]

h = 6,63∙10^-34 [Дж∙с]

ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

1. Расчет и построение температурной зависимости химического потенциала в электрон-вольтах:

Концентрация свободных электронов:

n = 8,464∙10²⁸ [1/м³]

Химический потенциал при T = 0 [К] в [эВ]:

μ₀ = 1,505 [эВ]

Температурная зависимость химического потенциала:

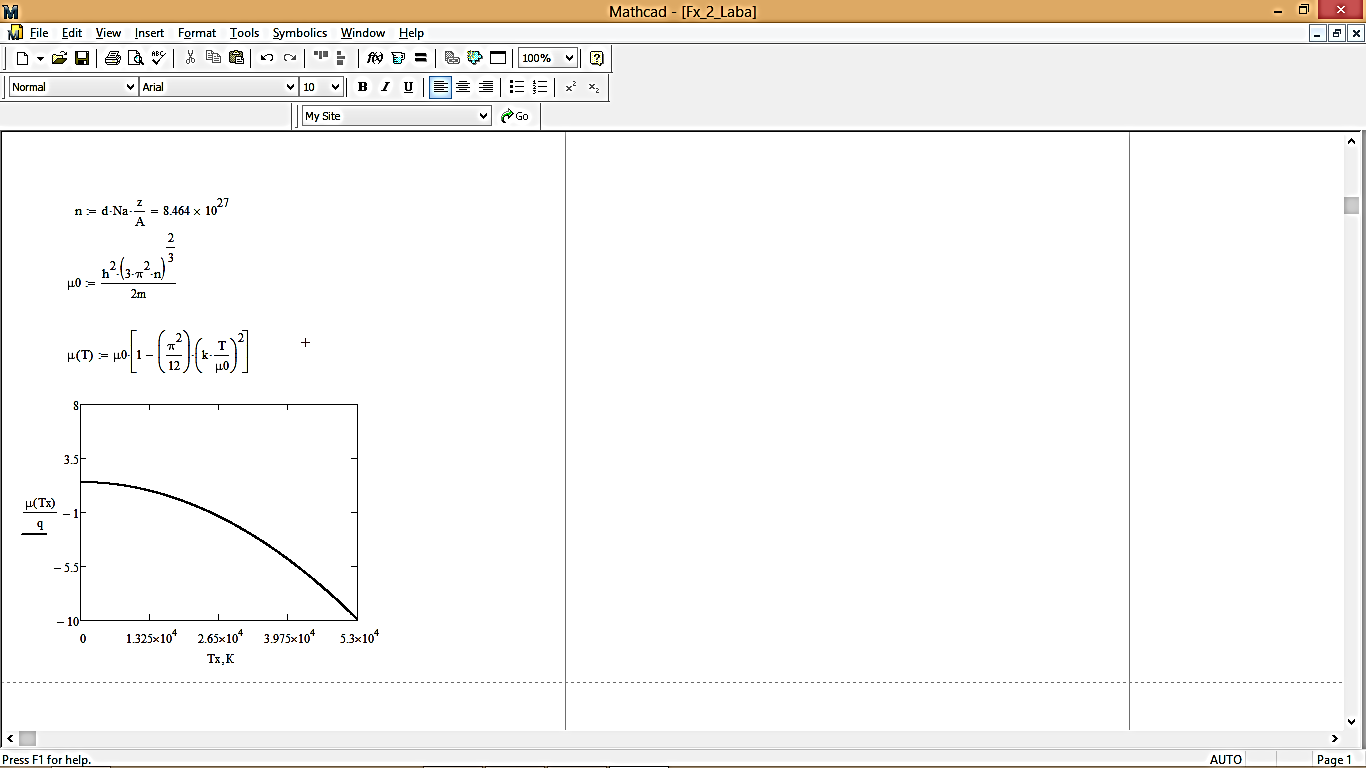
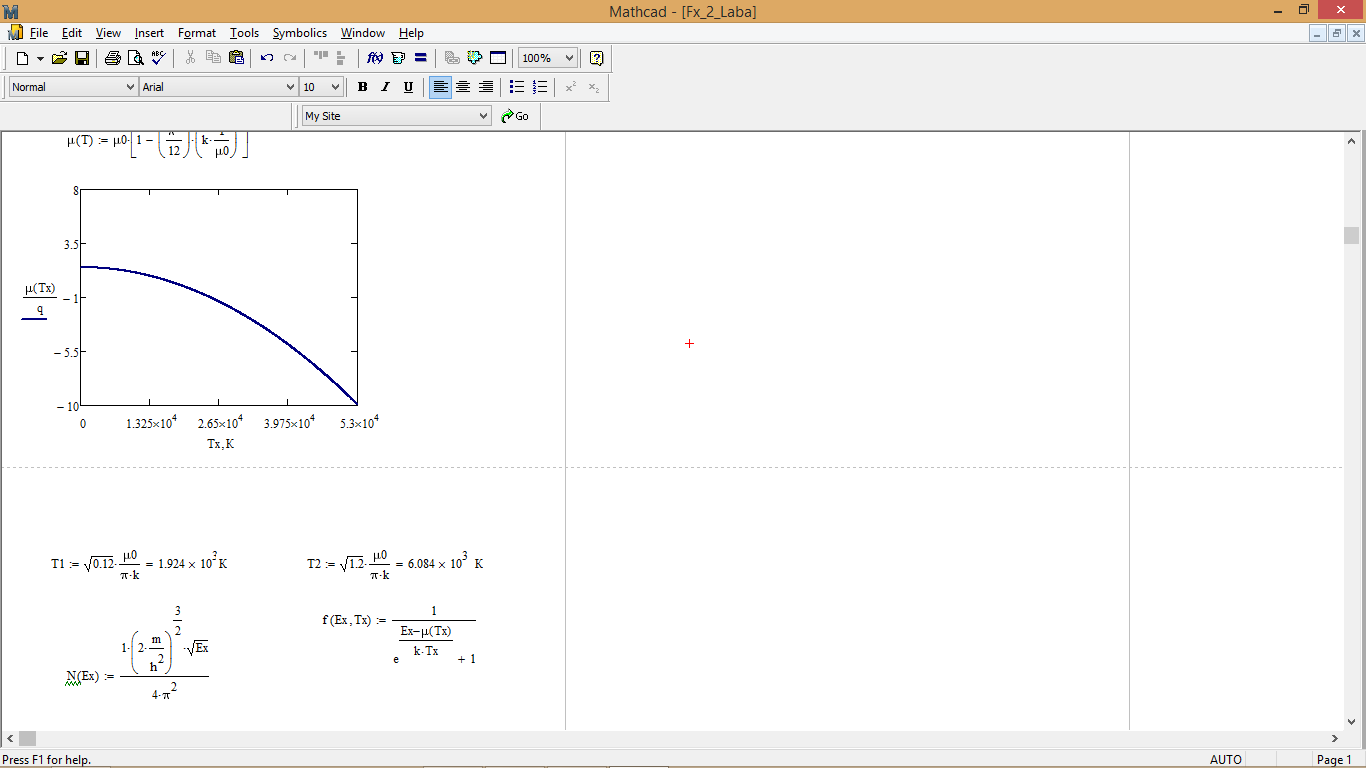
Рис. 1 – График температурной зависимости химического потенциала

Вычисление температуры, при которой химический потенциал будет отличаться от значения при 0 К на 1 %, 10 %:

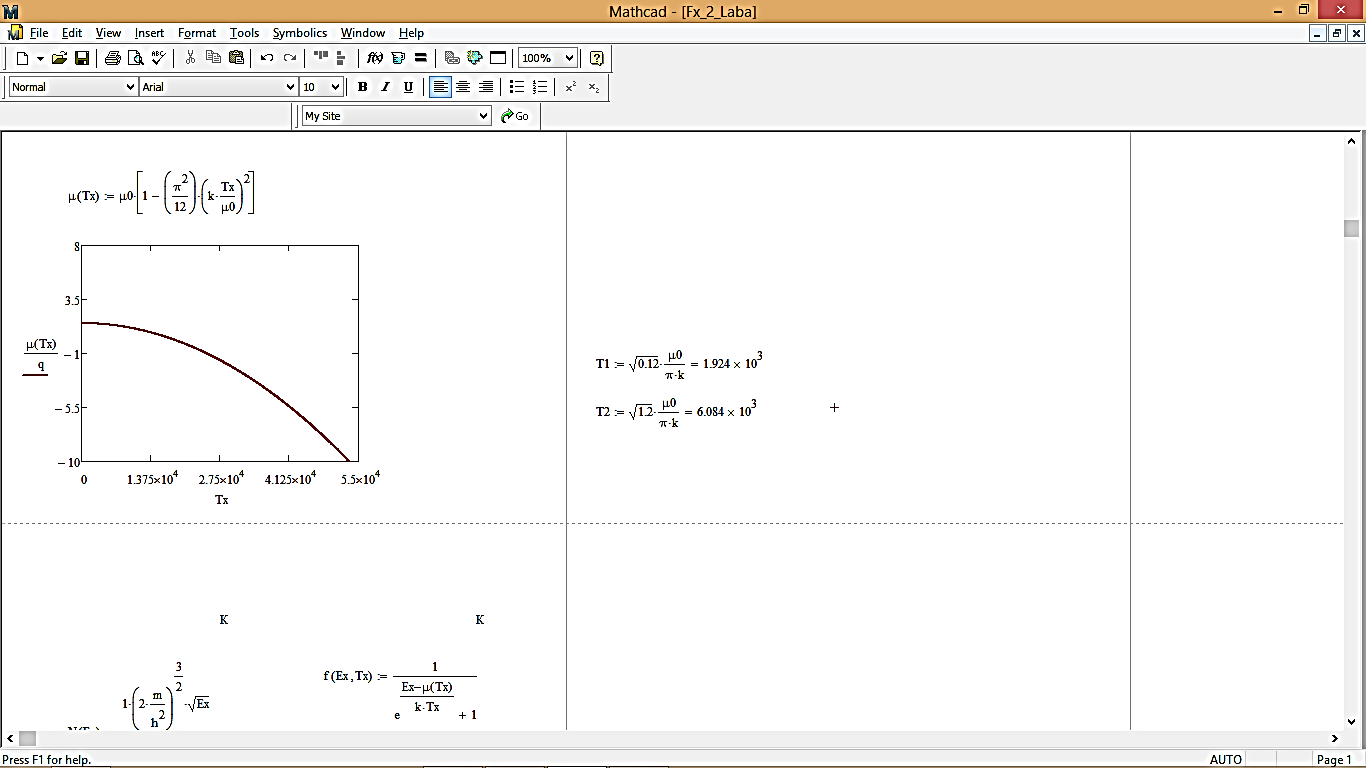
Таким образом, химический потенциал будет отличаться от значения при 0 К на 1% при: T₁ = 1,924∙10³ [К], на 10% при: T₂ = 6,084∙10³ [К]

2. Расчет плотности состояния, функции распределения Ферми-Дирака и распределения электронов по энергиям:

Плотность состояния:

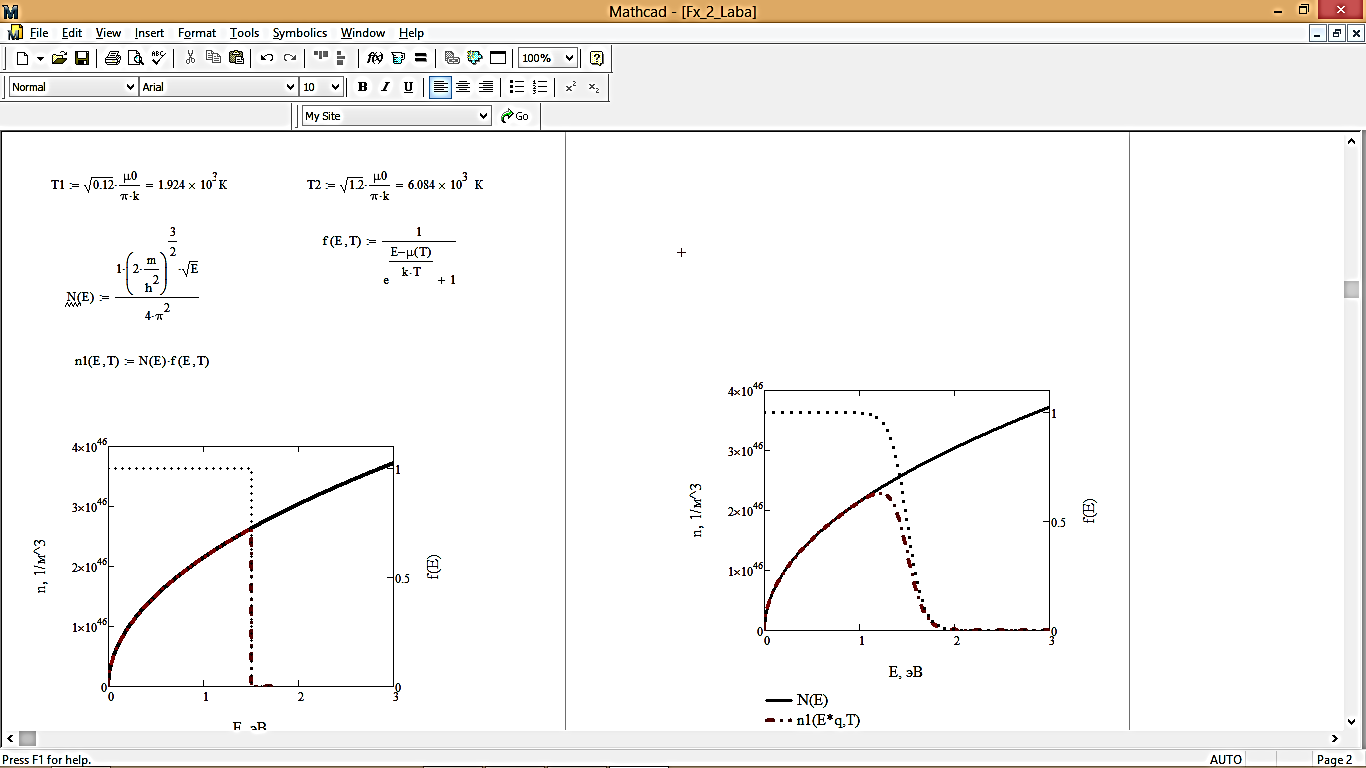
Распределение Ферми-Дирака:

Распределение электронов по энергиям:

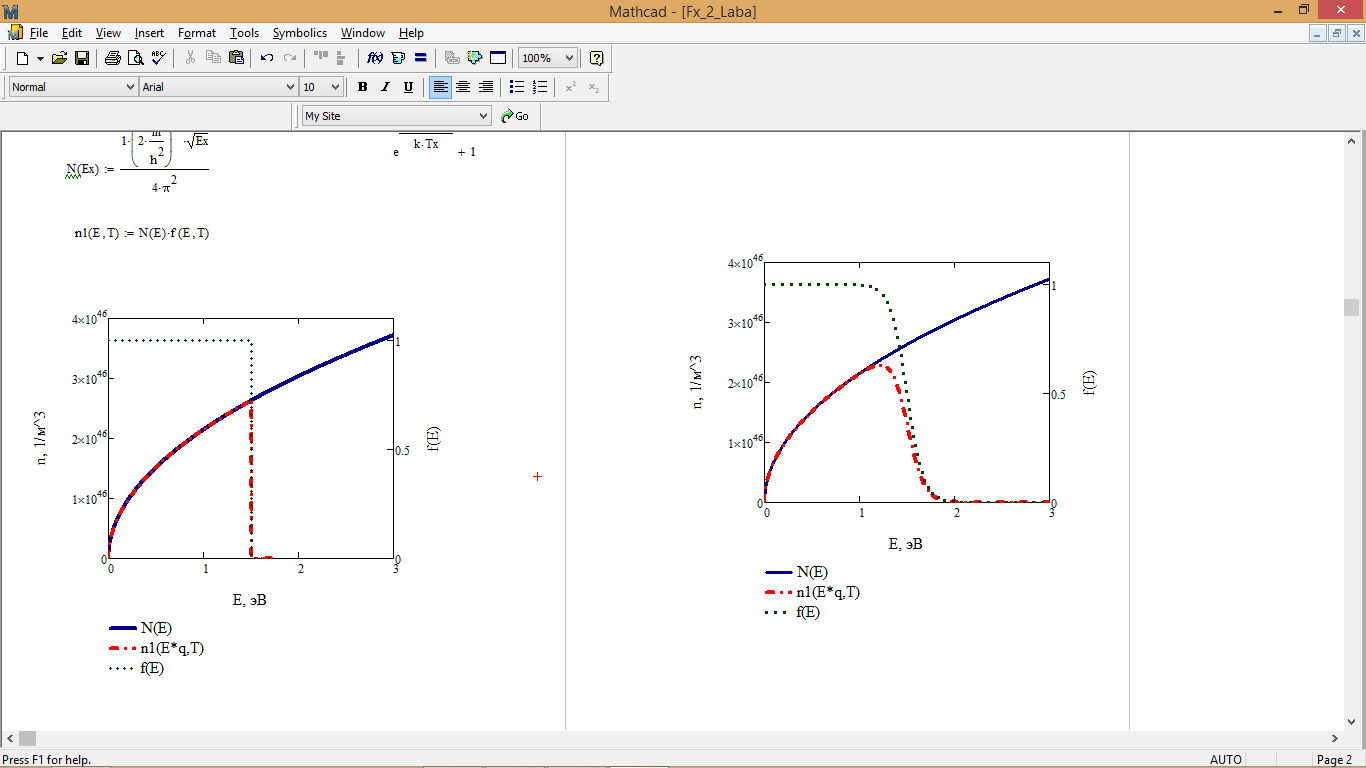
Рис. 2 – График плотности состояния, функции распределения Ферми-Дирака и распределения электронов по энергиям при T = 4 К

Рис. 3 – График плотности состояния, функции распределения Ферми-Дирака и распределения электронов по энергиям при T = 1000 К

3. Вычисление концентрации электронов:

По формуле:

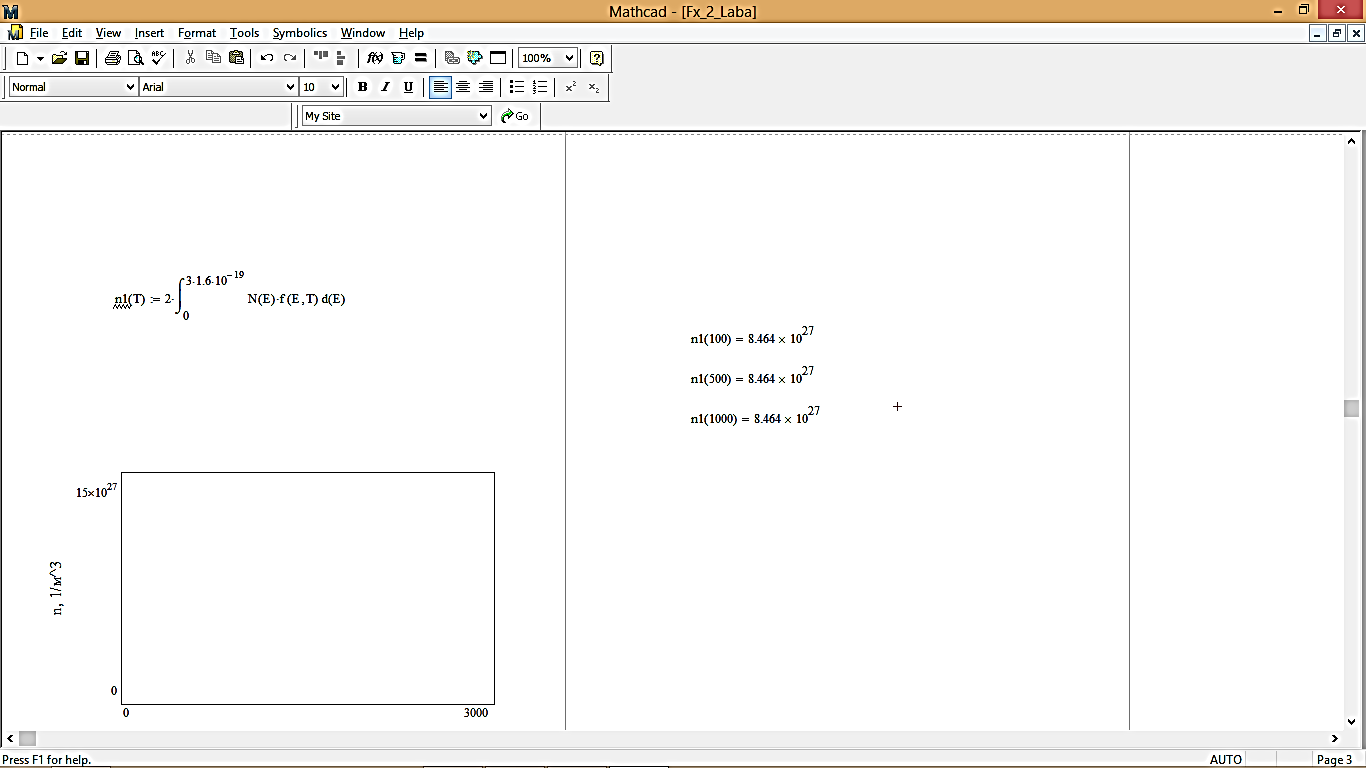
Значения концентрации для следующих значений температур (100 K; 500 К; 1000 К;):

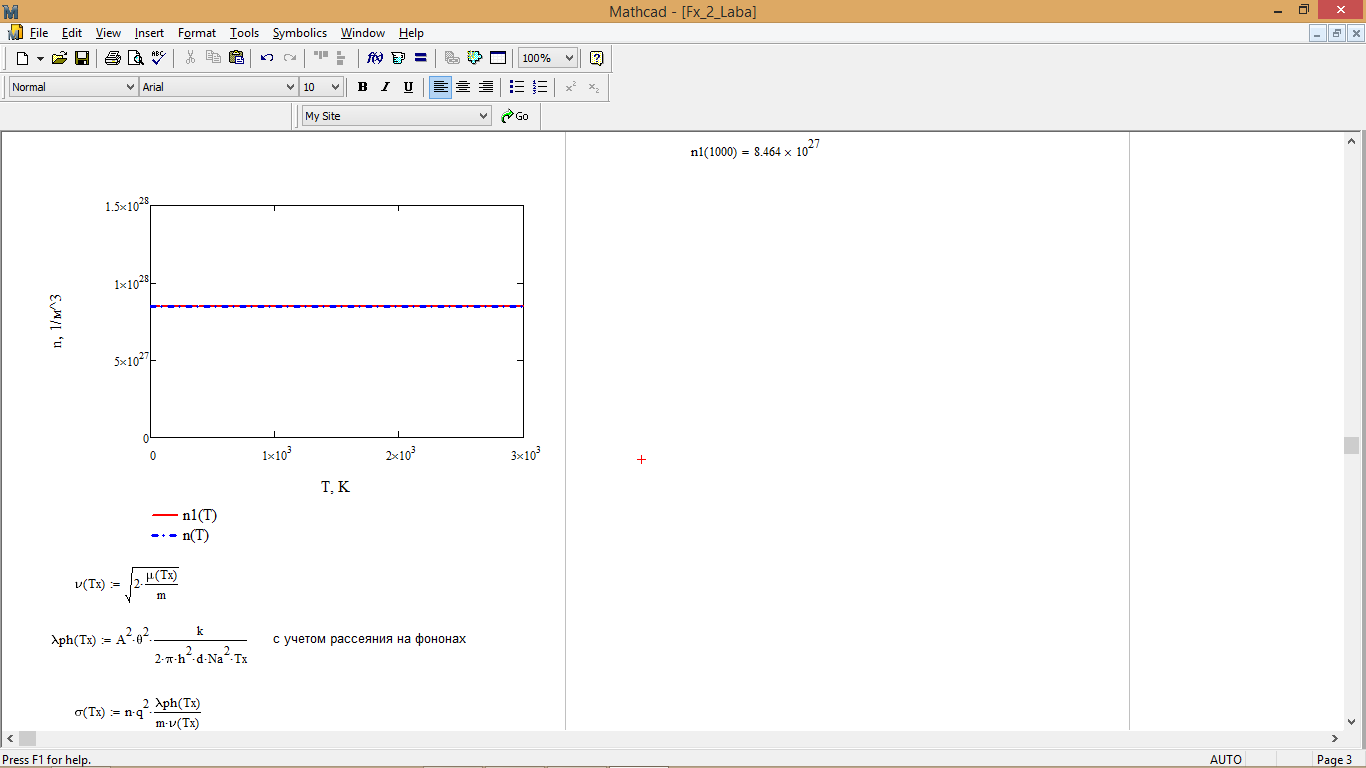
Рис. 4 - Концентрация электронов

Сравнивая полученное ранее значение n (концентрации свободных электронов), делаем вывод, что значения полностью совпадают.

4. Расчет длины свободного пробега с учетом электрон-фононного рассеяния:

По формуле:

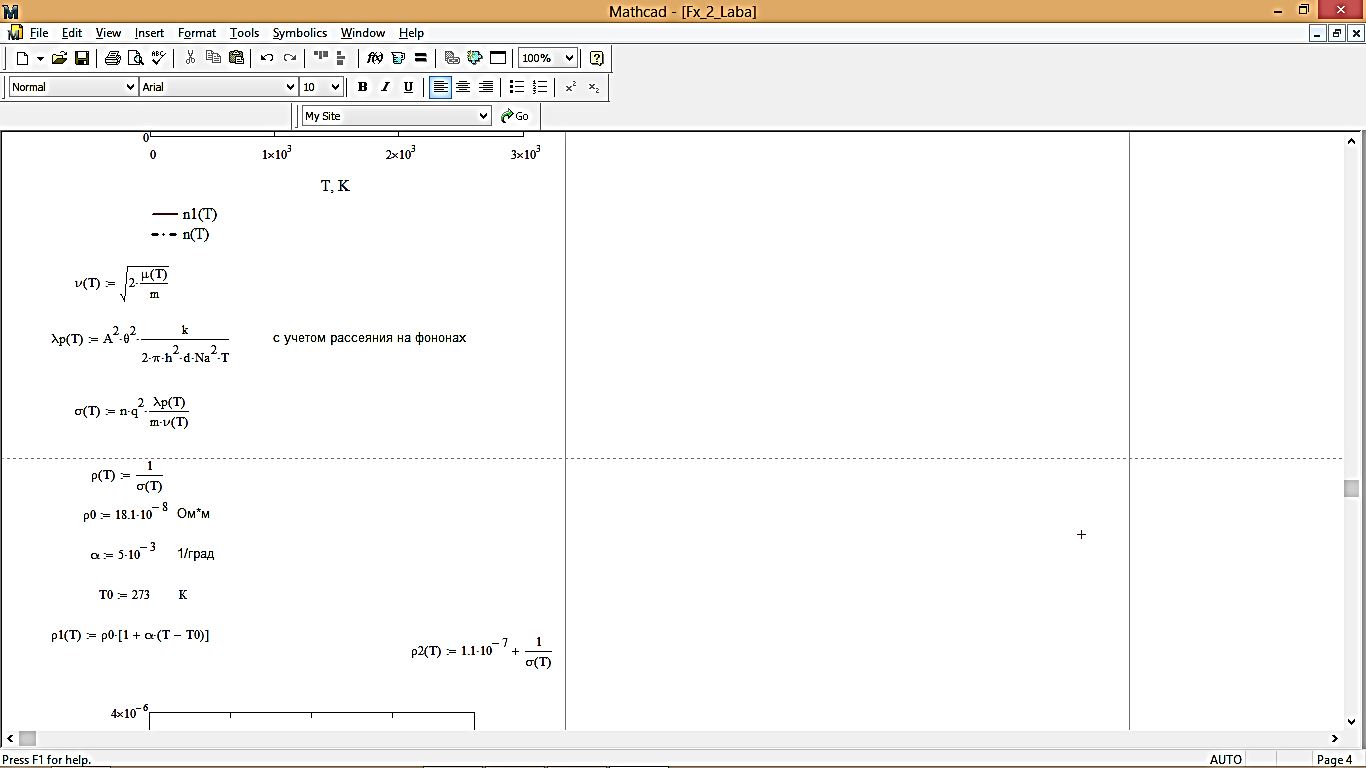
Скорость электронов:

Проводимость металла:

Удельное сопротивление металла:

Температурная зависимость удельного сопротивления на основе справочных данных:

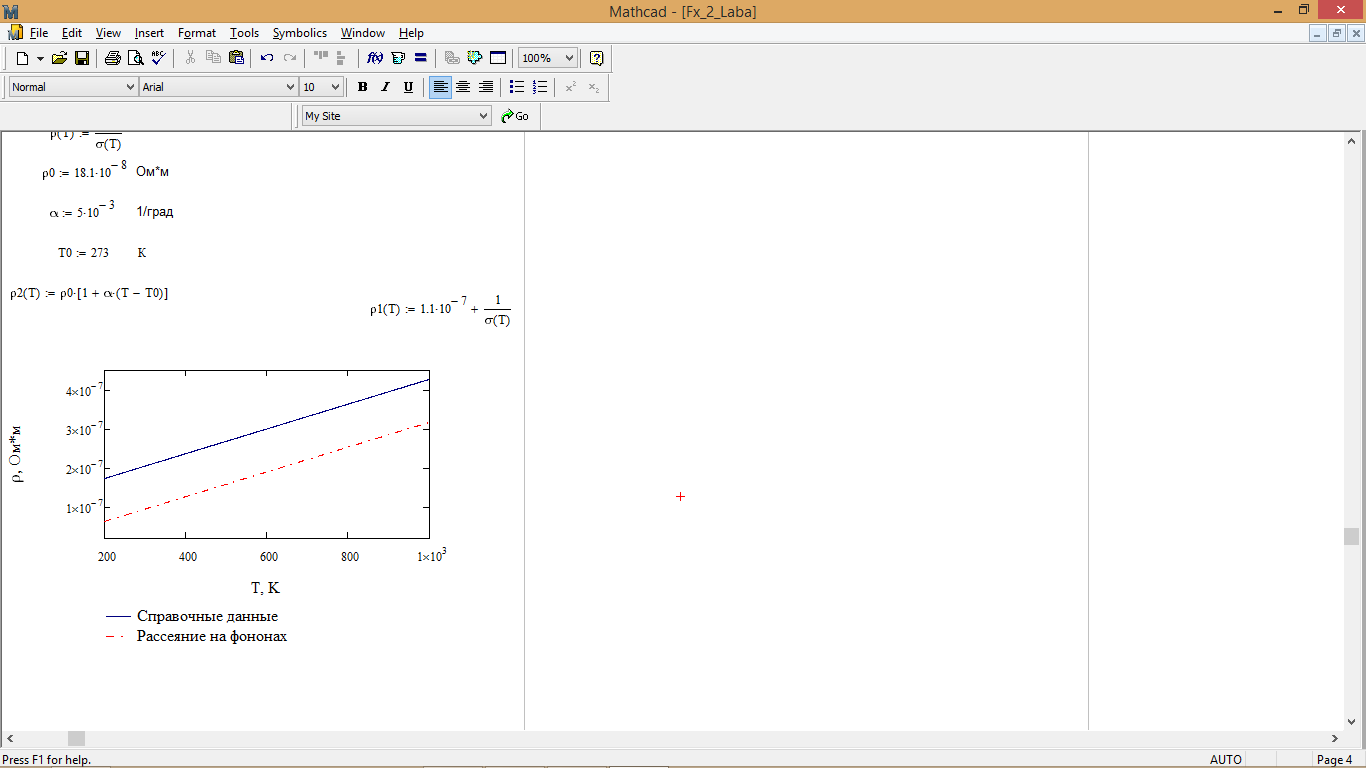
Рис. 5 - Температурные зависимости удельного сопротивления

Вклад дефектного рассеяния в величину удельного сопротивления металла для Т = 300 К:

ρ₁(300) – ρ(300) = 1,101∙10^-7 [Ом∙м]

Расчет длины свободного пробега различными способами при T=300 K:

Длина свободного пробега в случае электрон-фононного рассеяния:

λ_p(300) = 3,205∙10^-8 [м]

Длина свободного пробега на основе справочных данных:

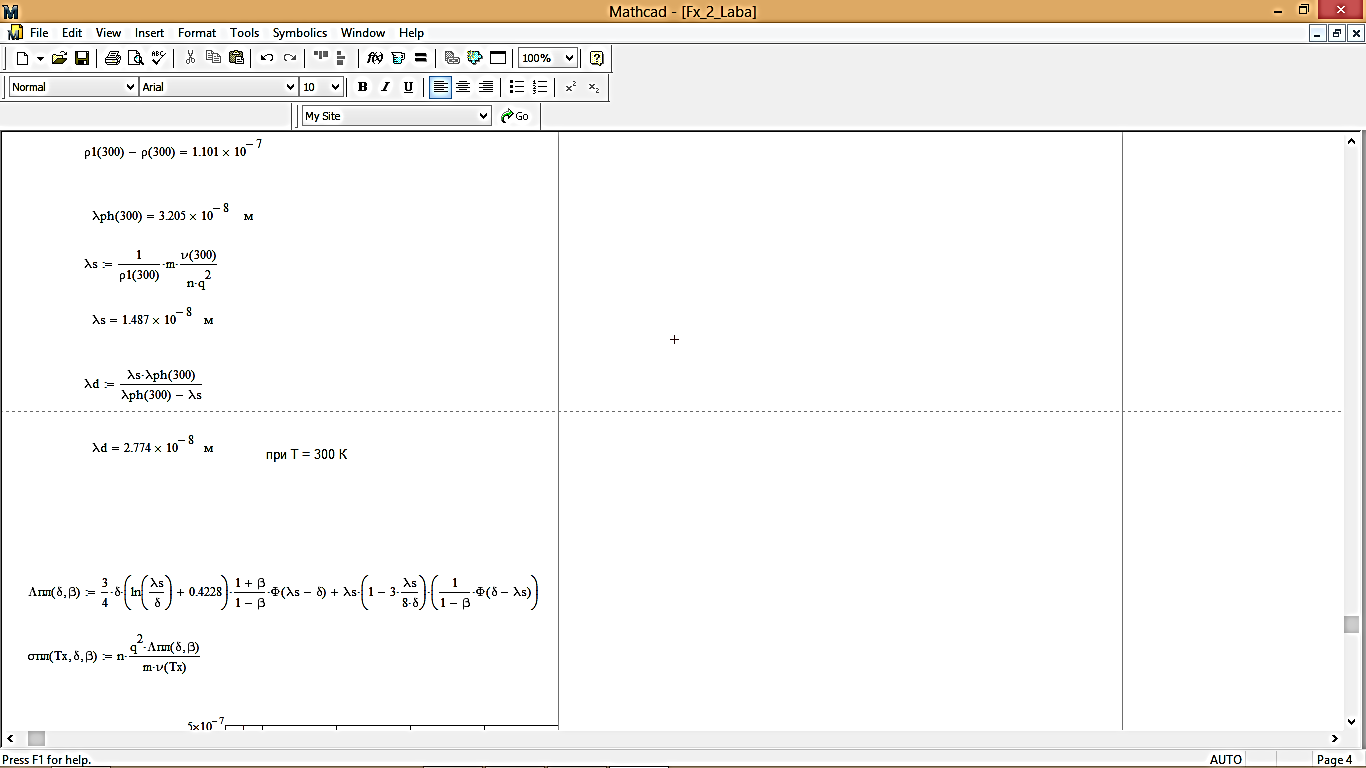
λ_s = 1,487∙10^-8 [м]

Длина свободного пробега, связанная только с дефектным рассеянием:

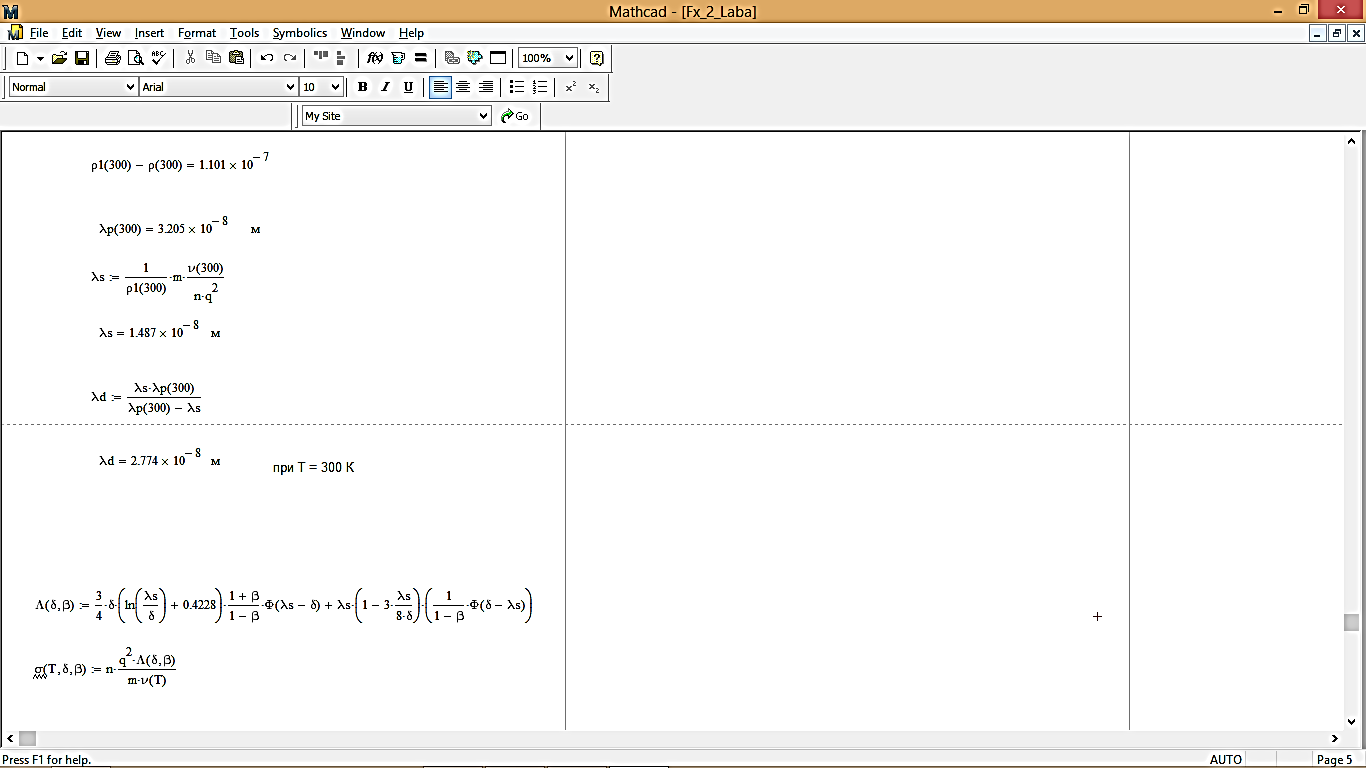
λ_d = 2,774∙10^-8 [м]

5. Зависимость удельного сопротивления металлической пленки от ее толщины при различных вероятностях зеркального отражения:

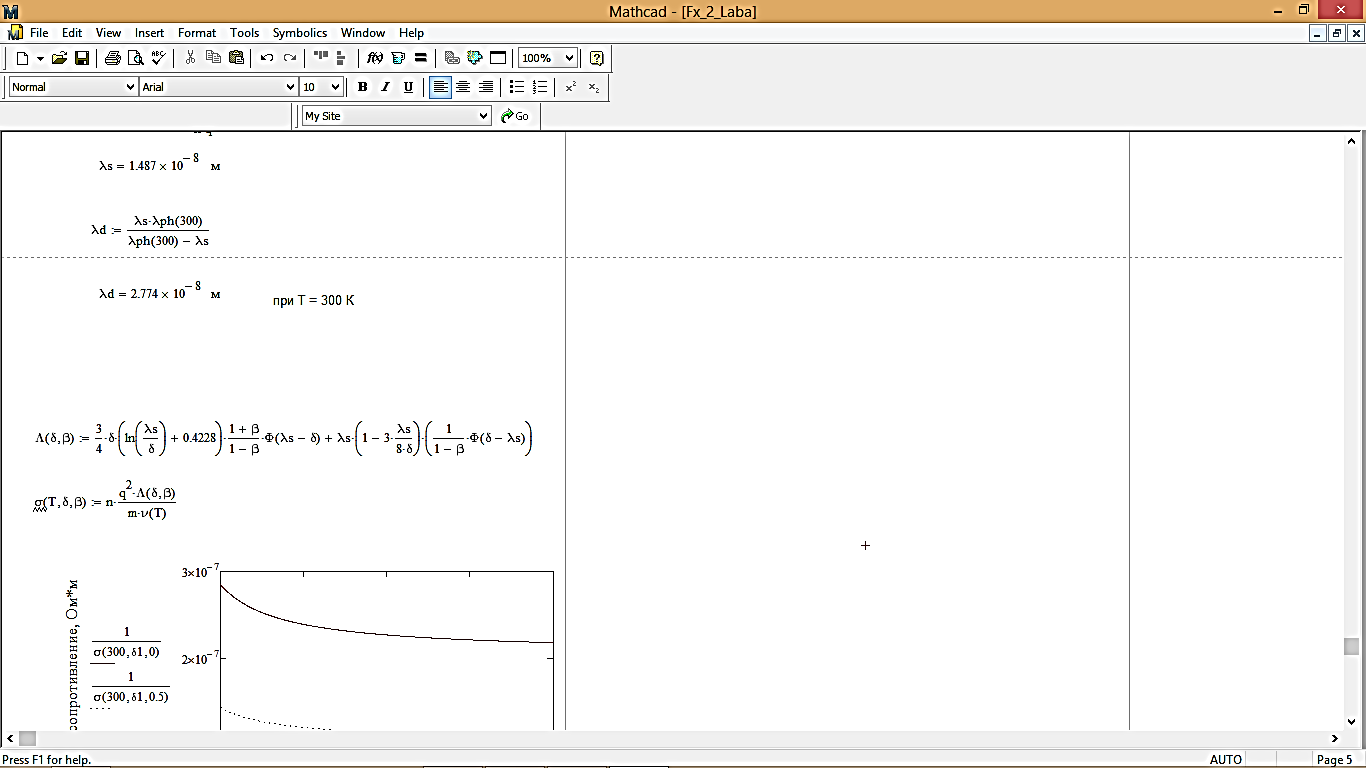
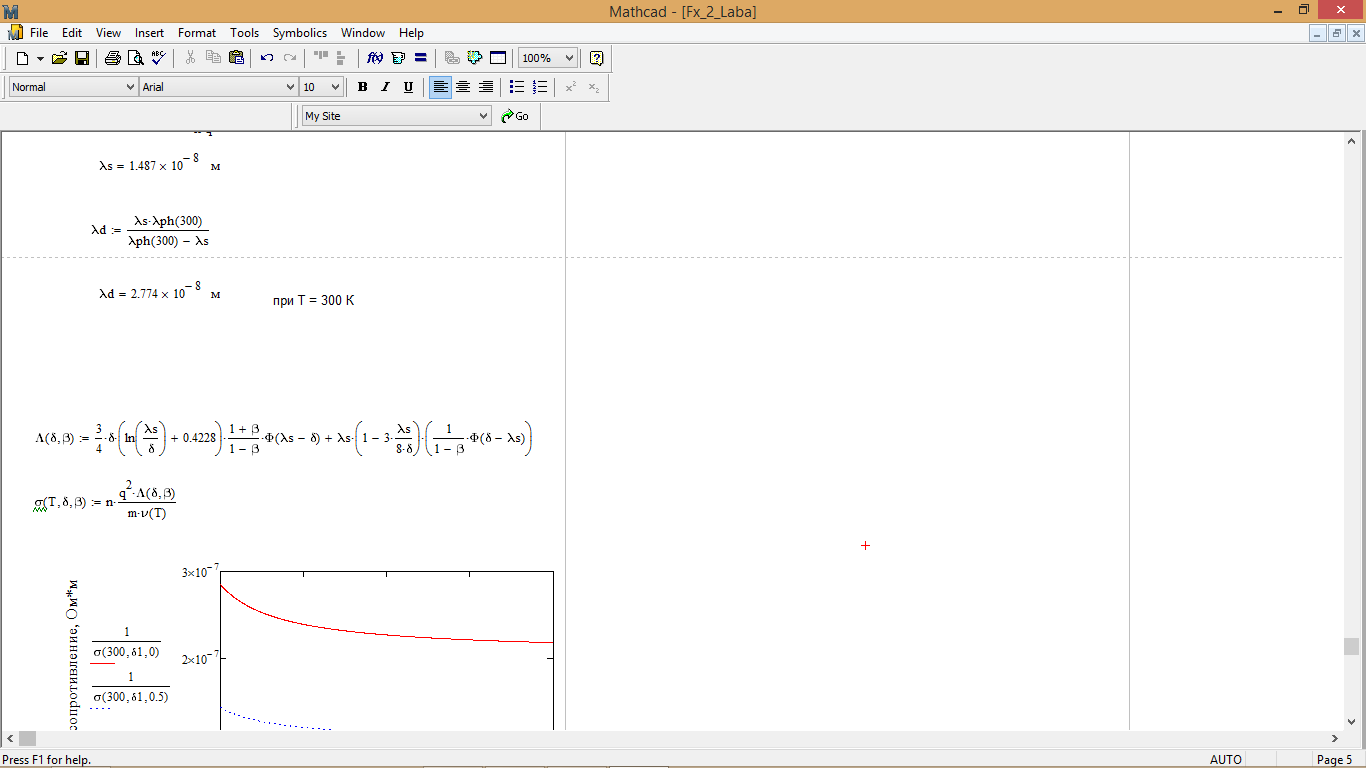
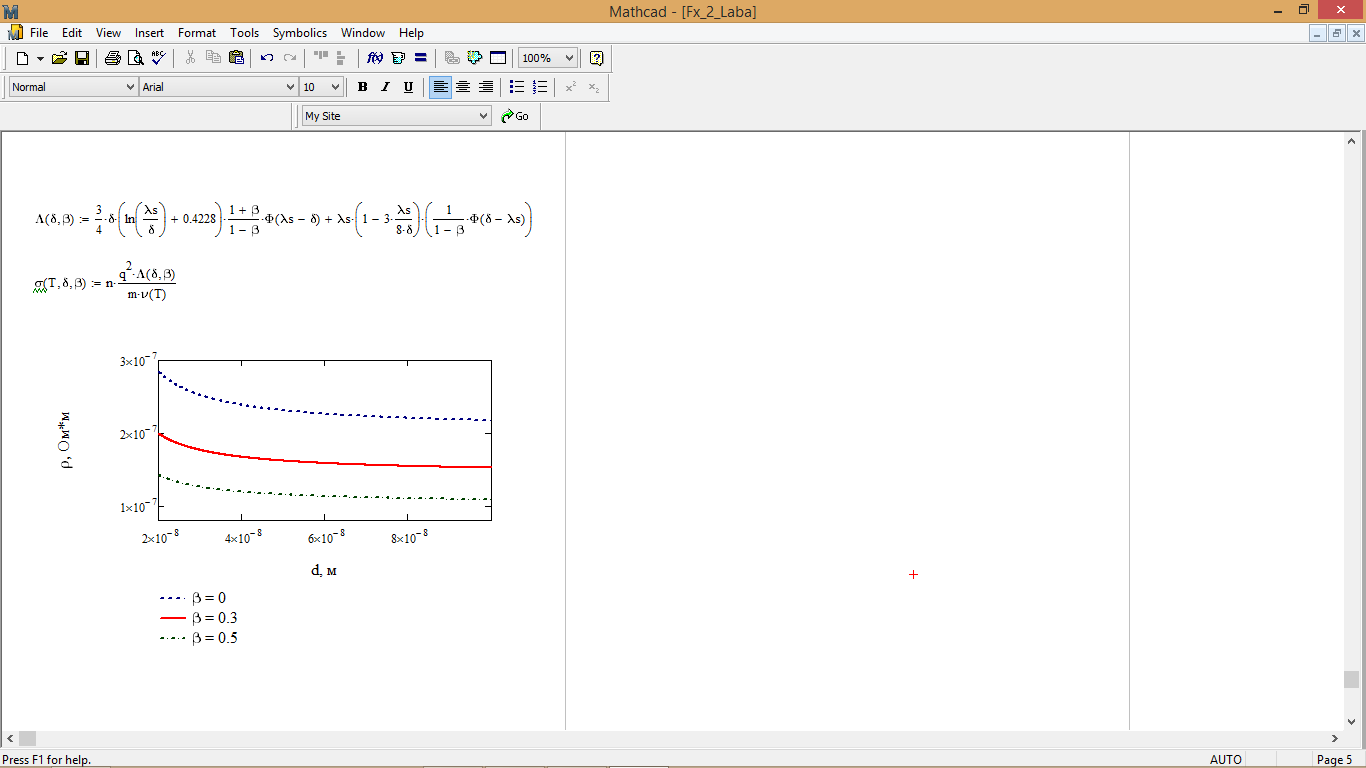
Рис. 6 - Зависимость удельного сопротивления металлической пленки от ее толщины

ВЫВОД

Анализируя график температурной зависимости химического потенциала (рис. 1), делаем вывод, что при повышении температуры величина химического потенциала уменьшается.

При этом, в случае повышения температуры уровень ферми «смещается» (рис. 2 и рис. 3), значит, в следствие данного факта, концентрация электронов по значениям энергии также изменяется.

Также, анализируя график концентрации электронов (рис. 4), делаем вывод, что концентрация электронов не зависит от температуры, при этом, значения, полученные путем интегрирования и рассчитанные по формуле сошлись.

Анализируя температурную зависимость удельного сопротивления (рис. 5), делаем вывод, что с увеличением температуре удельное сопротивление металла, в данном случае цезия (Cs) – возрастает. Данное увеличение значения удельного сопротивления связано с рассеянием на дефектах и электрон – фононным рассеянием.

Также анализируя зависимость удельного сопротивления металлической пленки от ее толщины (рис. 6), делаем вывод, что с увеличением толщины пленки удельное сопротивление уменьшается. Также, стоит заметить, что удельное сопротивление пленки уменьшается в результате увеличения вероятности зеркального отражения.