МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра фотоники
отчет
по лабораторной работе №1
по дисциплине «Физика твердого тела»
Тема: Определение температурной зависимости положения уровня ферми в полупроводниках
Вариант №7
Студент гр. 0207 _________________ Маликов Б.И.
Преподаватель _________________ Пухова В.М.
Санкт-Петербург
2022
ЦЕЛЬ РАБОТЫ
Целью работы является расчет зависимости уровня Ферми в невырожденном полупроводнике от температуры, а также концентрации и типа примеси.
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
Полупроводник – материал, который по своей удельной проводимости занимает промежуточное место между проводниками и диэлектриками, а также отличается от проводников сильной зависимостью удельной проводимости от ряда параметров: концентрации примесей, температуры и воздействия различных видов излучения. Полупроводники, или полупроводниковые соединения, бывают собственными и примесными.
Собственные полупроводники – это полупроводники, в которых нет примесей (доноров и акцепторов). Собственная концентрация (ni) – концентрация носителей заряда в собственном полупроводнике (электронов в зоне проводимости n и дырок в валентной зоне p, причем n = p = ni).
Примесный полупроводник – это полупроводник, электрофизические свойства которого определяются, в основном, примесями других химических элементов. Роль примесей могут играть и всевозможные дефекты структуры кристаллической решетки полупроводника, такие как вакансии, междуузельные атомы, дислокации.
На рис. 1 показана энергетическая схема полупроводника, содержащего как донорную, так и акцепторную примесь. Концентрации этих примесей равны, соответственно, Nd и Na.
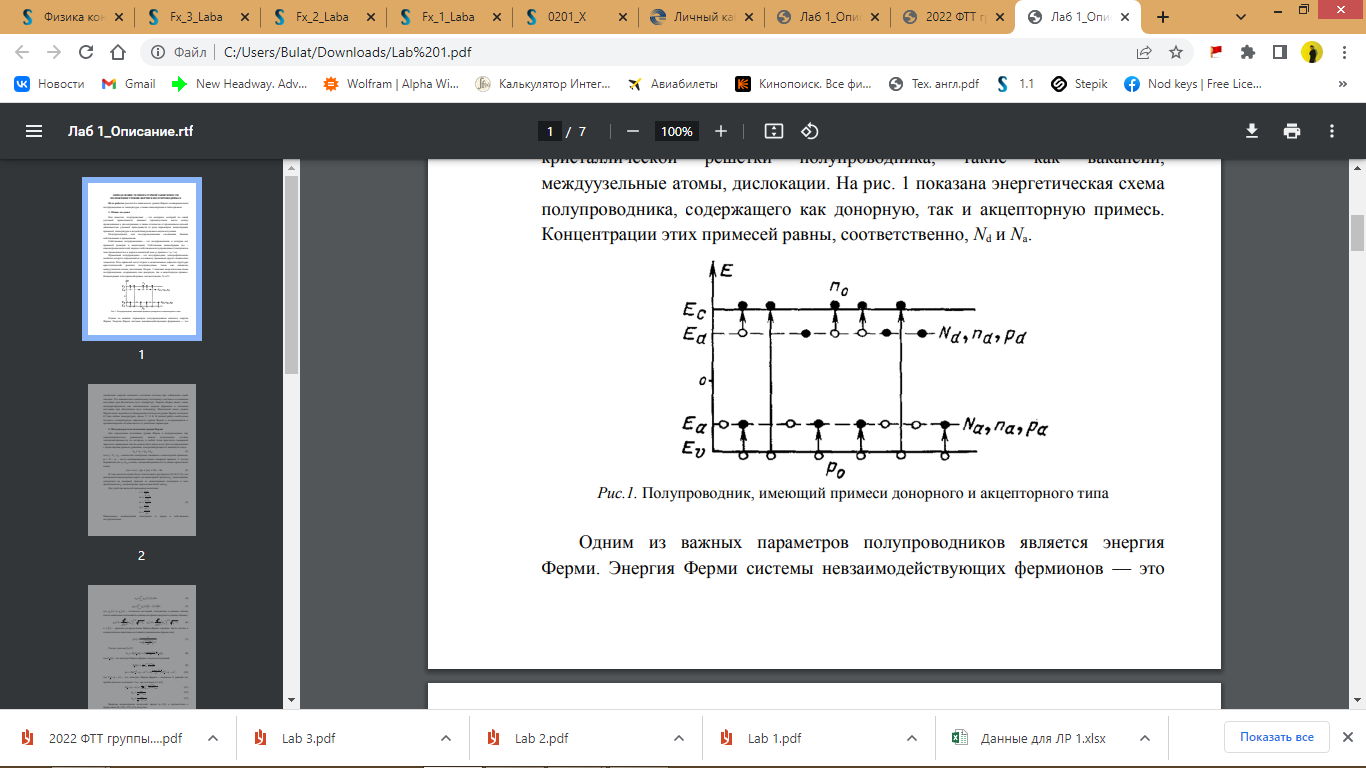
Рис. 1 - Полупроводник, имеющий примеси донорного и акцепторного типа
Одним из важных параметров полупроводников является энергия Ферми. Энергия Ферми системы невзаимодействующих фермионов — это увеличение энергии основного состояния системы при добавлении одной частицы. Это эквивалентно химическому потенциалу системы в ее основном состоянии при абсолютном нуле температур.
Энергия Ферми может также интерпретироваться как максимальная энергия фермиона в основном состоянии при абсолютном нуле температур. Физический смысл уровня Ферми таков: вероятность обнаружения частицы на уровне Ферми составляет 0,5 при любых температурах, кроме T = 0 К. В данной работе необходимо получить температурную зависимость уровня Ферми в полупроводнике и проанализировать её зависимость от различных параметров.
Для конкретного случая ND=1012 см-3 и T=300 K уровень Ферми для кремния расположен у края зоны проводимости ниже энергии связи донорного состояния, так что почти все донорные центры при этом оказываются ионизированными (рис. 2).
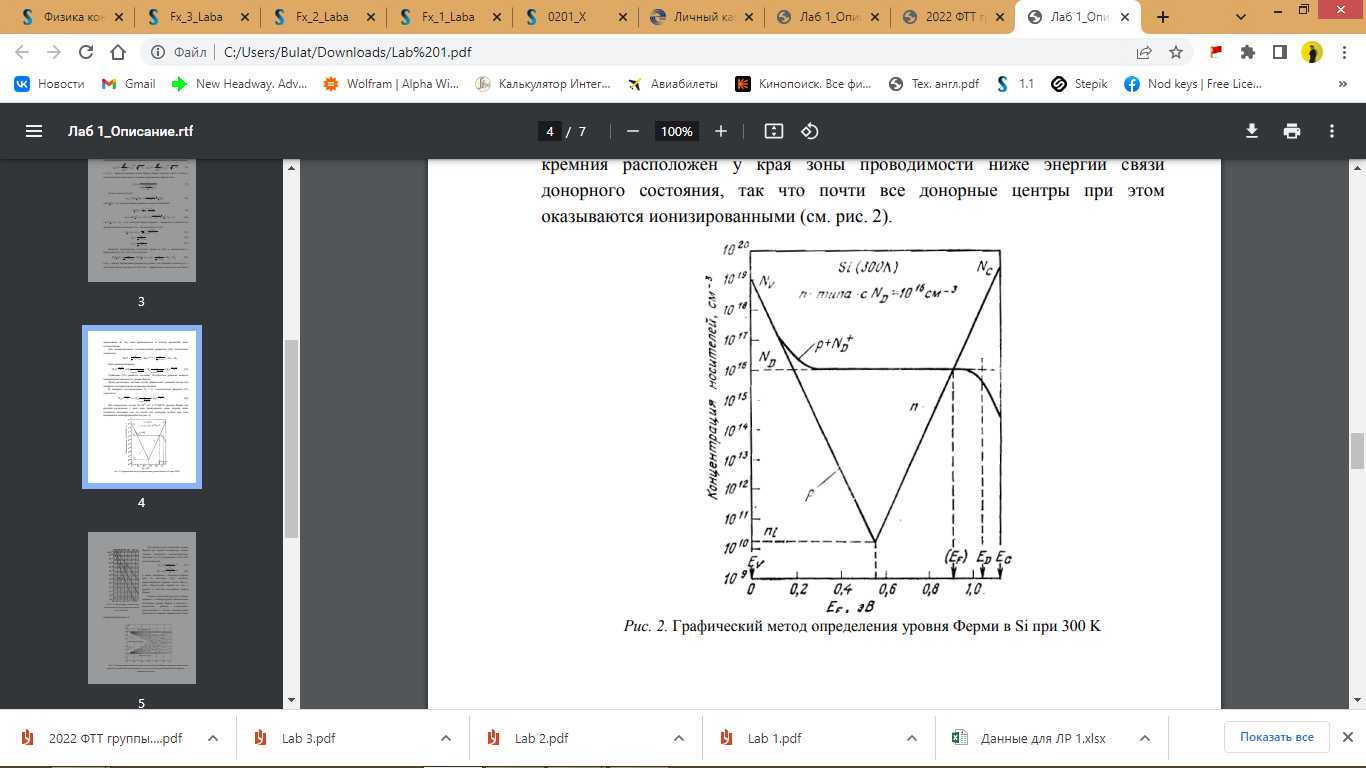
Рис. 2 - Графический метод определения уровня Ферми в Si при 300 K
Д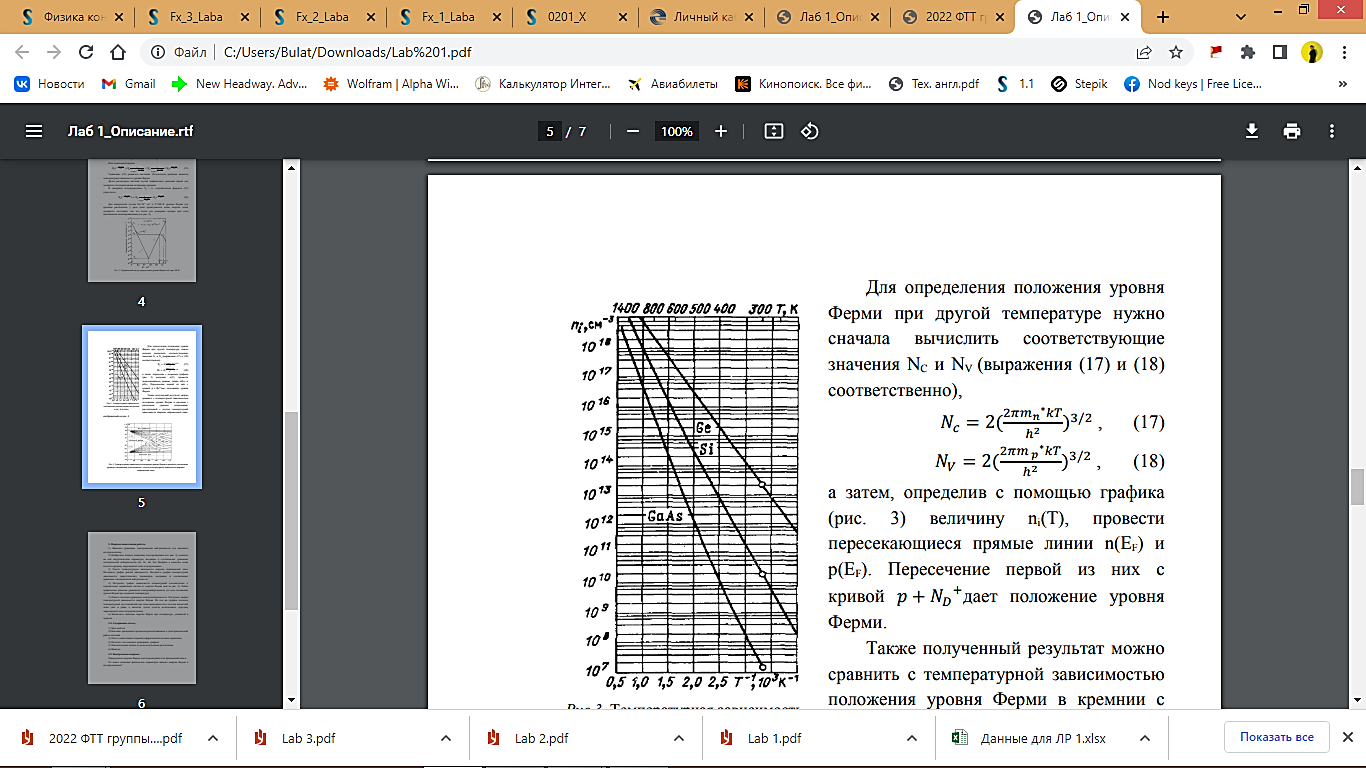
ля
определения положения уровня Ферми при
другой температуре нужно сначала
вычислить соответствующие значения NC
и NV
(выражения (1) и (2) соответственно):
(1)
(2)
а затем, определив с помощью графика (рис. 3) величину ni(T), провести пересекающиеся прямые линии n(EF) и p(EF). Пересечение первой из них с кривой p + ND+ . дает положение уровня Ферми.
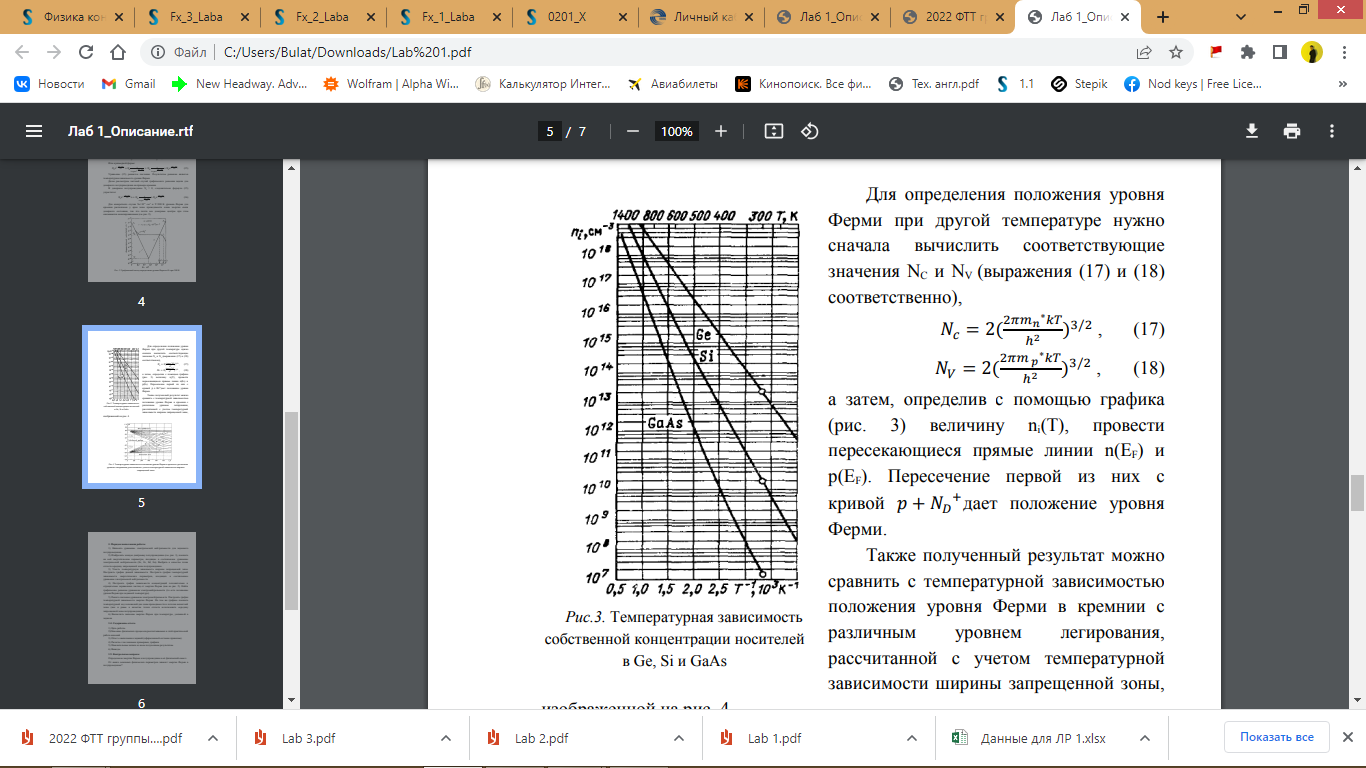
Рис. 3 - Температурная зависимость собственной концентрации носителей в Ge, Si и GaAs
Также полученный результат можно сравнить с температурной зависимостью положения уровня Ферми в кремнии с различным уровнем легирования, рассчитанной с учетом температурной зависимости ширины запрещенной зоны, изображенной на рис. 4.
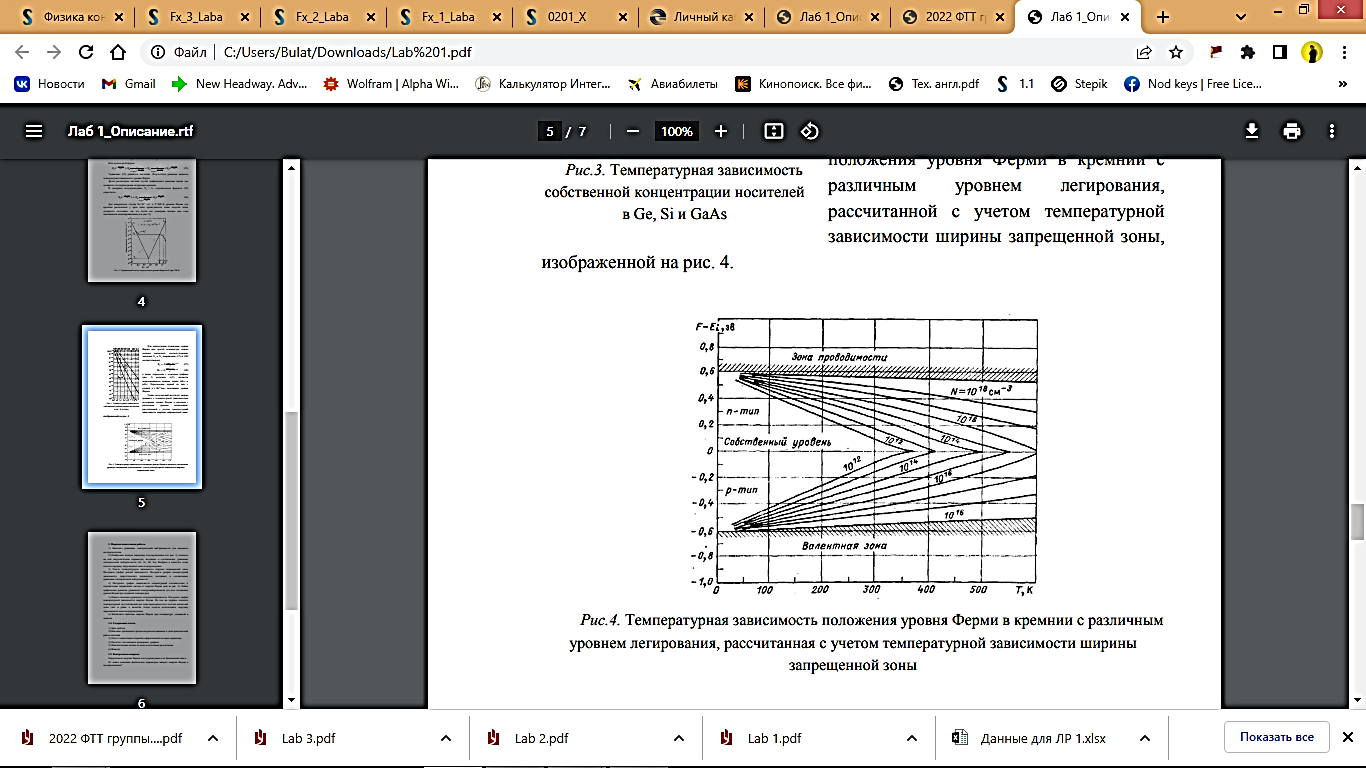
Рис. 4 - Температурная зависимость положения уровня Ферми в кремнии с различным уровнем легирования, рассчитанная с учетом температурной зависимости ширины запрещенной зоны
ДАННЫЕ ДЛЯ ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ
Табл. 1
Исходные данные
Материал |
Примесь |
Тип |
Концентрация, см-3 |
Температура, К |
Кремний Si |
Индий In |
Акцептор |
Na = 6∙1016 |
420 |
k = 1,38∙10-23 [Дж/К] = 8,617∙10-5 [эВ]
m = 9,1∙10-31 [кг]
mn = 0,33∙m [кг]
mp = 0,81∙m [кг]
h = 6,63∙10-34 [Дж∙с]
ga = 4
Ea0 = 0,16 [эВ]
Eg(0) = 1,170 [эВ]
α = 4,73∙10-4 [эВ/К]
β = 636
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
1. Уравнение электрической нейтральности для заданного полупроводника:
2. Зонная диаграмма полупроводника:
Eg(0) = 1,170 [эВ] - ширина запрещенной зоны
Ev
=
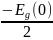= − 0,585 [эВ] - «потолок» валентной
зоны
Ec
=
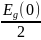= 0,585 [эВ] - «дно» зоны проводимости
Ea = Ev + Ea0 = − 0,585 + 0,16 = − 0,425 - энергия активации
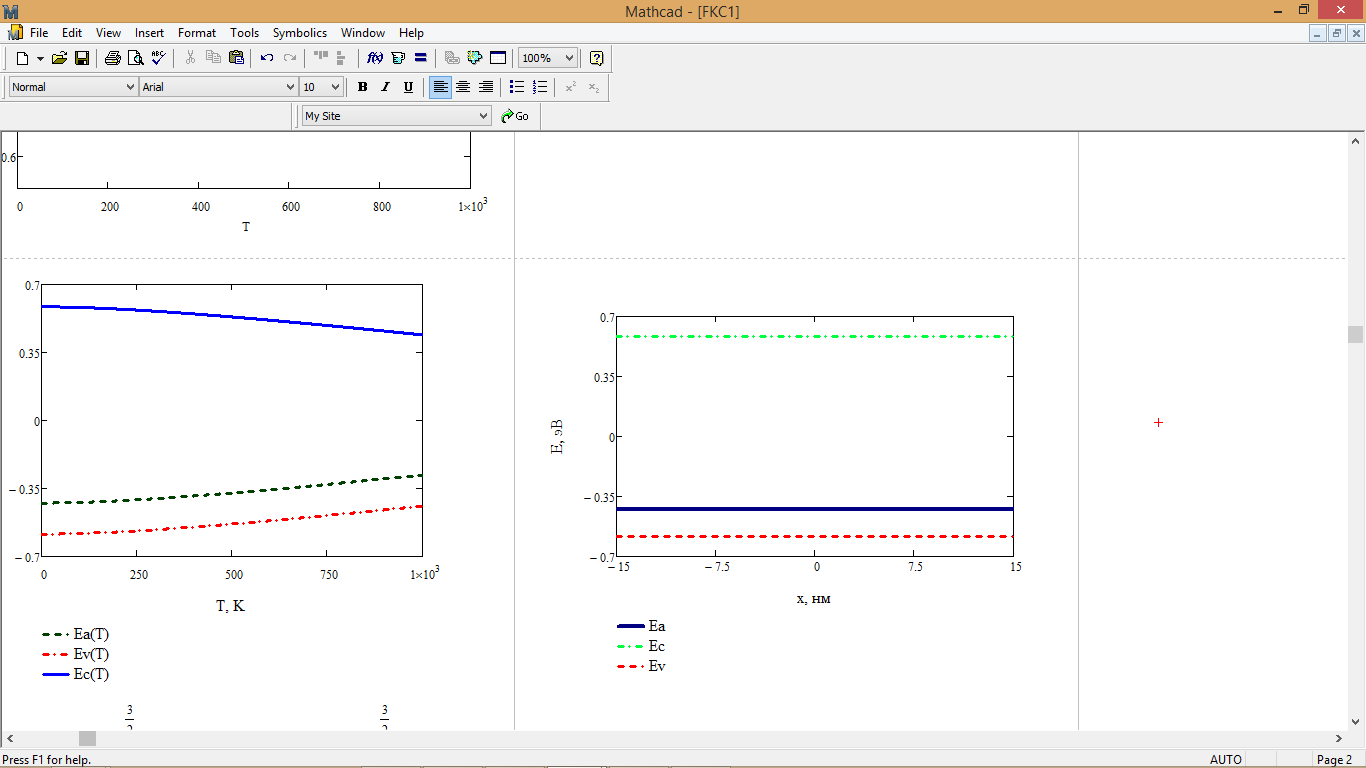
Рис. 5 – Зонная диаграмма полупроводника
3. График температурной зависимости ширины запрещенной зоны, также график температурной зависимости энергетических параметров, входящих в составленное уравнение электрической нейтральности:
Температурная зависимость ширины запрещенной зоны определяется по формуле:
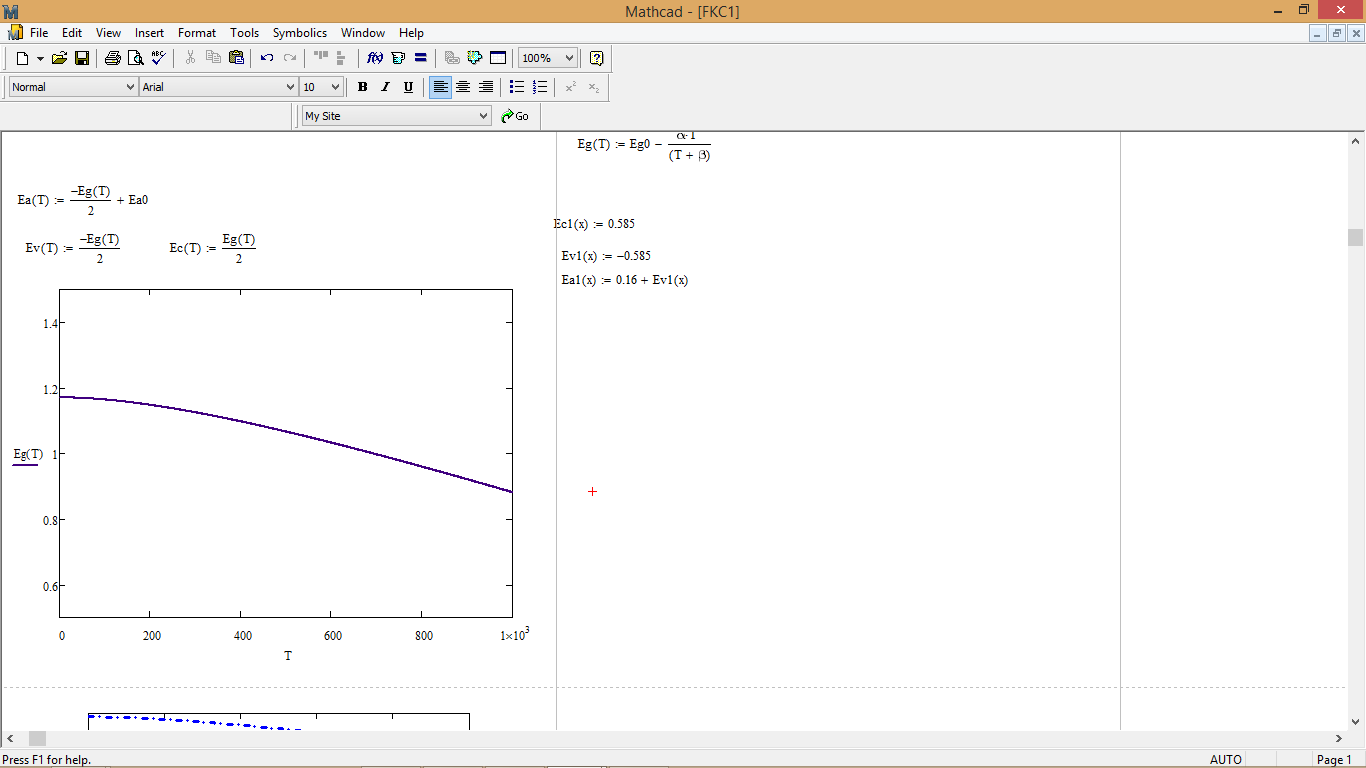
Рис. 6 - График температурной зависимости ширины запрещенной зоны
Вычисление энергетических параметров, входящих в уравнение электронейтральности:
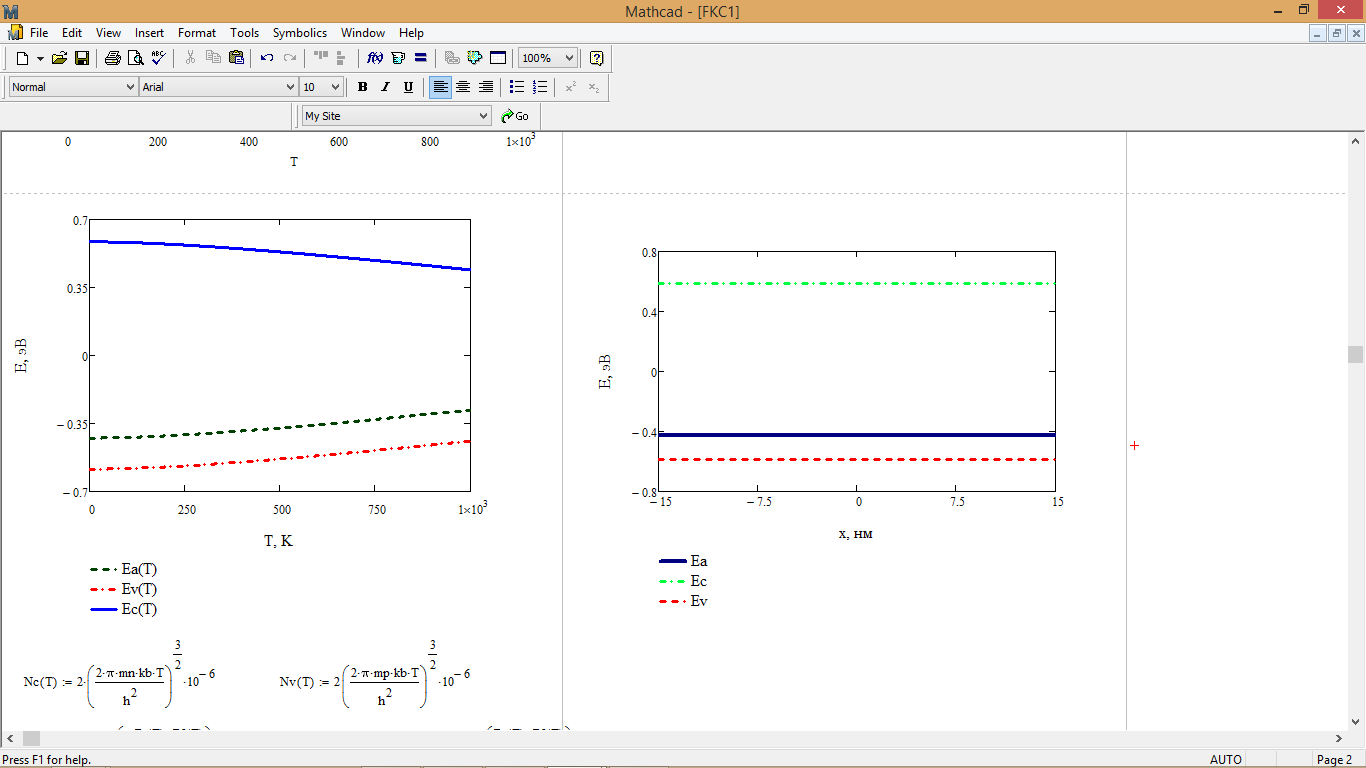
Рис. 7 - График температурной зависимости энергетических параметров
5. Графическое решение уравнение электронейтральности:
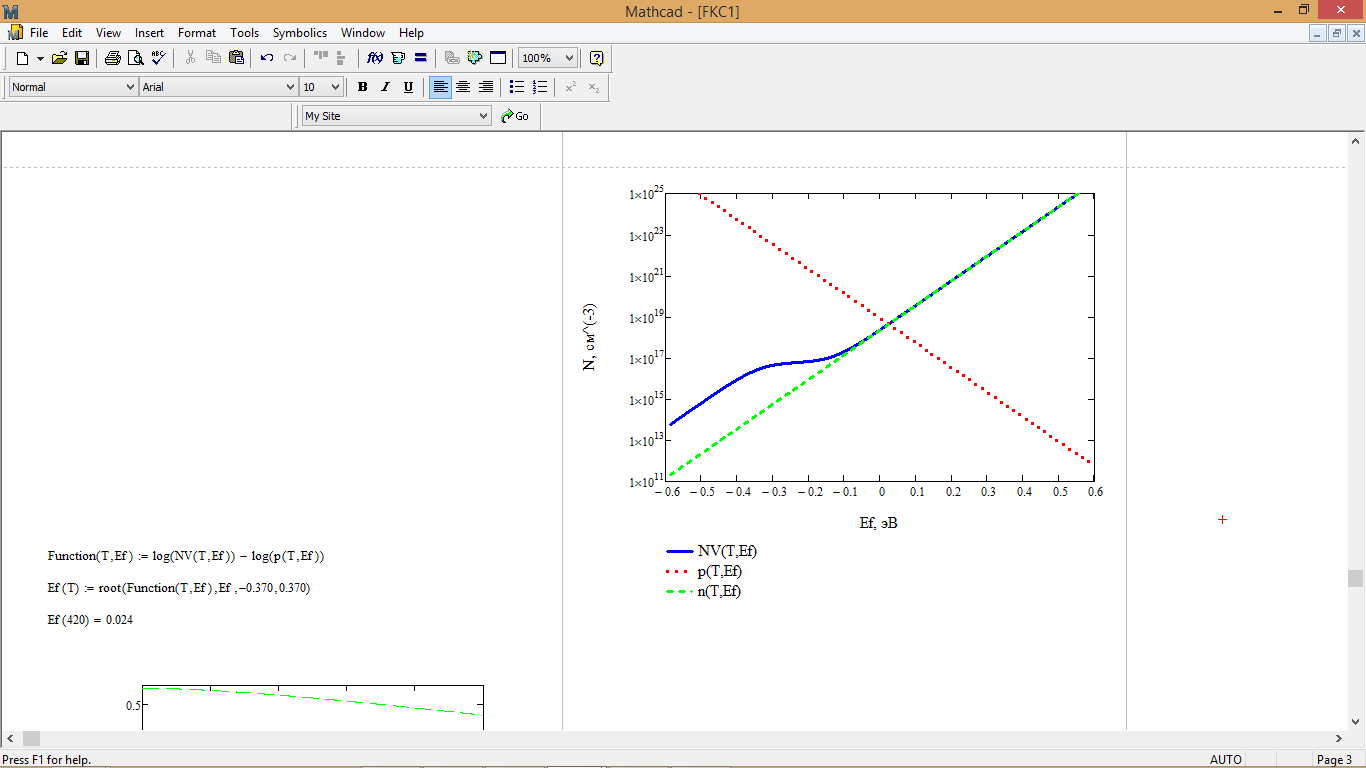
Рис. 8 – Определение уровня Ферми графическим методом
Таким образом, определяя точку пересечения графиков:
Ef ≈ 0,025 [эВ]
6. Численное решение уравнения электронейтральности:
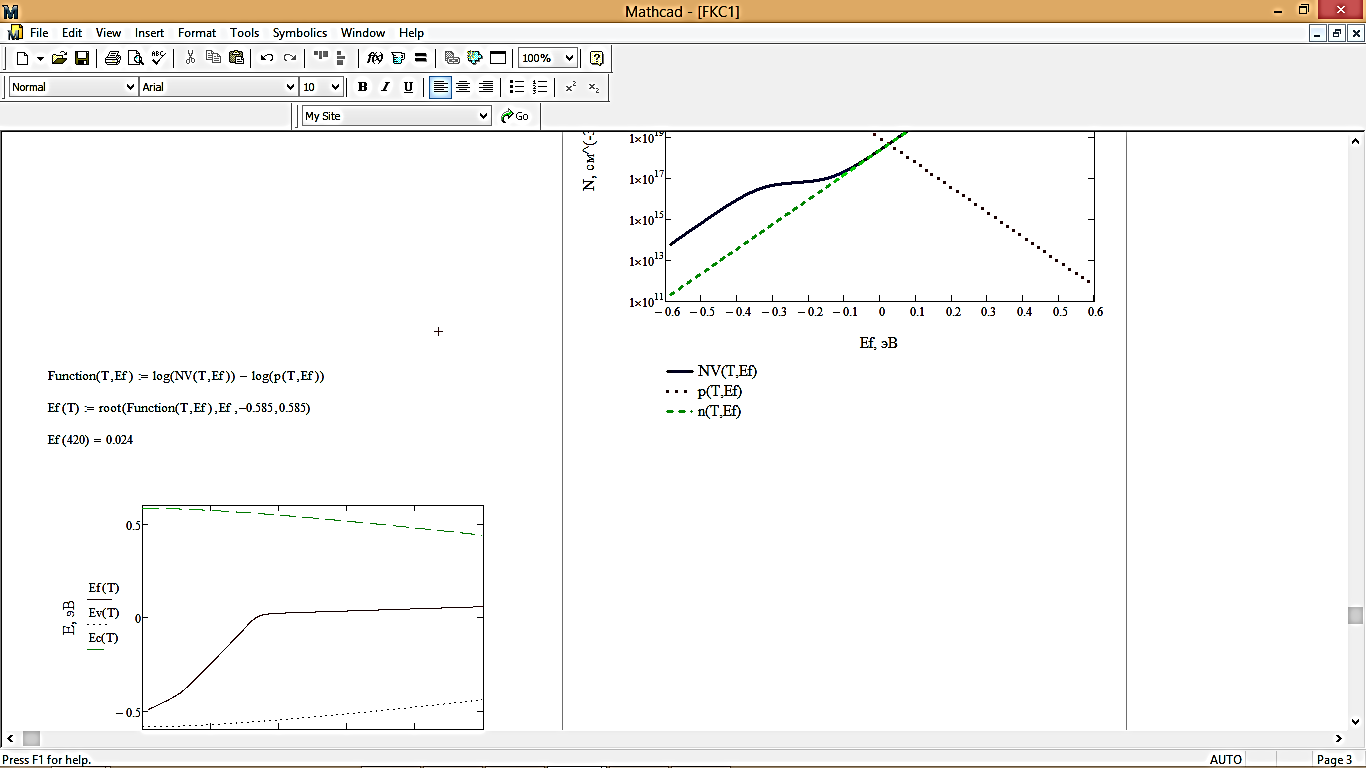
Сравнивая графическое и численное значения, делаем вывод, что значения приблизительно равны, что говорит о верном определении Ef.
7. Температурная зависимость энергии Ферми:
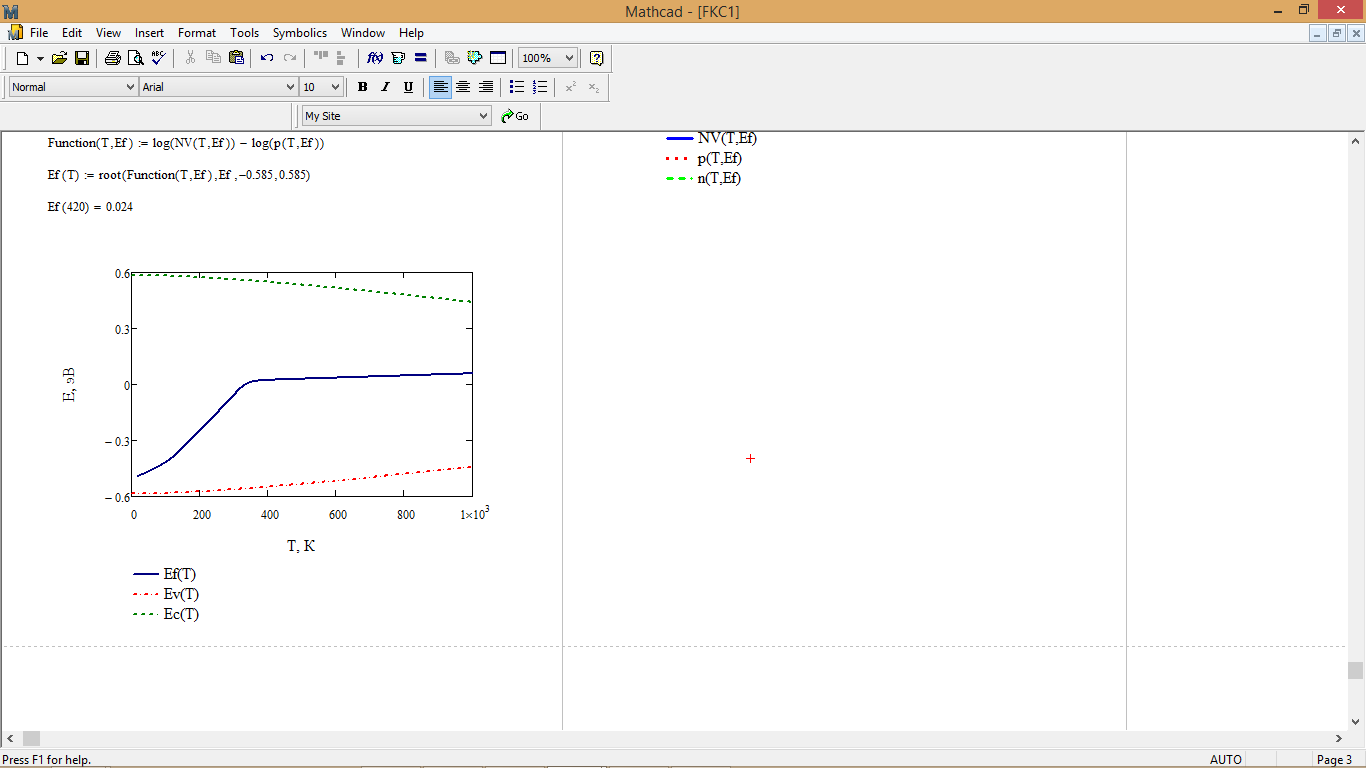
Рис. 9 – График температурной зависимости энергии Ферми
ВЫВОД
В результате проведения данной лабораторной работы, было получено значения энергии Ферми, определенное двумя методами (графическим –
Ef = 0,025 [эВ] и численным – Ef = 0,024 [эВ]). При этом, сравнивая оба метода, делаем вывод о приблизительном совпадении полученных значений Ef, что говорит о верности наших вычислений.
Также, были получены температурные зависимости энергии Ферми (рис. 9) и ширины запрещенной зоны (рис. 6). Анализируя оба графика, делаем вывод, что с ростом температуры ширина запрещенной зоны уменьшается, при этом, энергия Ферми увеличивается, и, с 400 К энергия Ферми плавно изменяется, что говорит о переходе примесного полупроводника в из примесной в собственную проводимость.