ИДЗ / ИДЗ 7 / IDZ7_MalikovBI_0207

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра физической электроники и технологии

Индивидуальное домашнее задание №7

Студент гр. 0207 _________________ Маликов Б.И.

Преподаватель _________________ Никитин А.А.

Санкт-Петербург

2023

ЗАДАНИЕ

Найти максимальную толщину пленки алюминия, осажденную за время 100 с. Пленка осаждается методом термического испарения из кольцевого источника диаметром 5 см и температурой 1200 К. Расстояние от источника до подложки 8 см.

ИСХОДНЫЕ ДАННЫЕ

Материал: Al

Плотность: ρ = 2,71∙10³ кг/м³

Молярная масса: M = 26,98∙10^-3 кг/моль

Температура: T = 1200 K

Коэффициент А: A = 8,99 (так как температура подложки T = 1200 K – 273 K = 927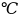 ближе всего подходит к интервалу температур: 724-1279 )

Коэффициент B: B = 15630 K

Время осаждения: t = 100 с

Диаметр кольцевого источника: d = 5 см = 0,05 м

Расстояние от источника до подложки: h = 8 см = 0,08 м

РЕШЕНИЕ

1. Вычисление значения давления насыщенного пара

Вычислим значение давления насыщенного пара, используя коэффициенты A и B:

P_Н.П = 133∙ = 133∙ = 0,01227 Па = 12,27∙10^-3 Па

2. Вычисление массовой плотности потока алюминия

Массовая плотность потока Al вычисляется как:

J_m =

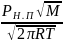
Отсюда, массовая плотность потока Al будет равна:

J_m = = 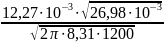= 8,052∙10^-6

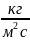
2. Нахождение максимальной толщины пленки алюминия

Радиус кольцевого источника равен:

s = 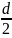= = 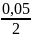0,025 м

Тогда:

s = 0,035

Значит:

h > s => 0,08 > 0,035 => Имеем один максимум в центре подложки

Выражение для толщины пленки, получаемой из кольцевого источника, выглядит следующим образом:

L =

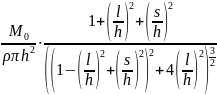
Так как максимальная толщина будет в центре подложки, то есть l = 0, и тогда формула принимает следующий вид:

L_maх = =

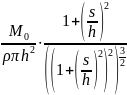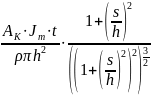
где A_K = 2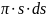 – площадь бесконечно тонкого кольца.

Примем толщину кольца намного меньше его радиуса, то есть: ds << s. Так как радиус кольца равняется: s = 0,025 м, тогда примем толщину кольца, равную 1 мм, то есть: ds = 1 мм = 0,001 м.

Тогда, площадь кольца будет равна:

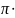A_K = 2 = 2 0,025∙0,001 = 0,000157 м²

Отсюда, максимальная толщина пленки алюминия равна:

L_maх = 1,93∙10^-9 м = 1,93 нм