ИДЗ / ИДЗ 1 / IDZ1_MalikovBI_0207

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра физической электроники и технологии

Индивидуальное домашнее задание №1

Студенты гр. 0207 _________________ Маликов Б.И.

Преподаватель _________________ Никитин А.А.

Санкт-Петербург

2023

ЗАДАНИЕ

а) Вычислите значение 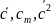, 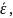и постройте распределения Максвелла по абсолютным скоростям f(с) и энергиям f(ε), постройте те же распределения в нормированных координатах, используя для нормировки среднюю скорость и кинетическую энергию, соответственно.

б) Найти число частиц, которые при максимальной температуре (или максимальной массе) имеют скорости в диапазонах 1 м/c и 100 м/c в окрестностях , а также энергию в диапазонах 1 мэВ и 30 мэВ в окрестности

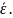
в) Построить зависимость числа соударений молекул газа с площадкой площадью 1 мм² за время 10 с.

ИСХОДНЫЕ ДАННЫЕ

Углекислый газ (CO₂)

Давление: p = 1 Торр = 1 мм. рт. ст. = 133 Па

Температурный диапазон: T = 400 – 600 К

Молярная масса: M = 44 г/моль = 44∙10^-3 кг/моль

Постоянная Больцмана: k = 1,38∙10^-23 Дж/К = 8,62∙10^-5 эВ/К

Постоянная Авогадро: N_A = 6,02∙10²³ моль^-1

Масса молекулы: m = 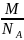= = 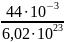7,309∙10^-26 кг

РЕШЕНИЕ

1. Вычисление значений , построение распределения Максвелла по абсолютным скоростям f(с) и энергиям f(ε), построение тех же распределений в нормированных координатах, используя для нормировки среднюю скорость и кинетическую энергию, соответственно

1.1.1 Вычисление значений 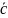(разделим температурный диапазон на три равные части)

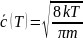
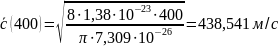
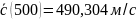
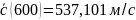
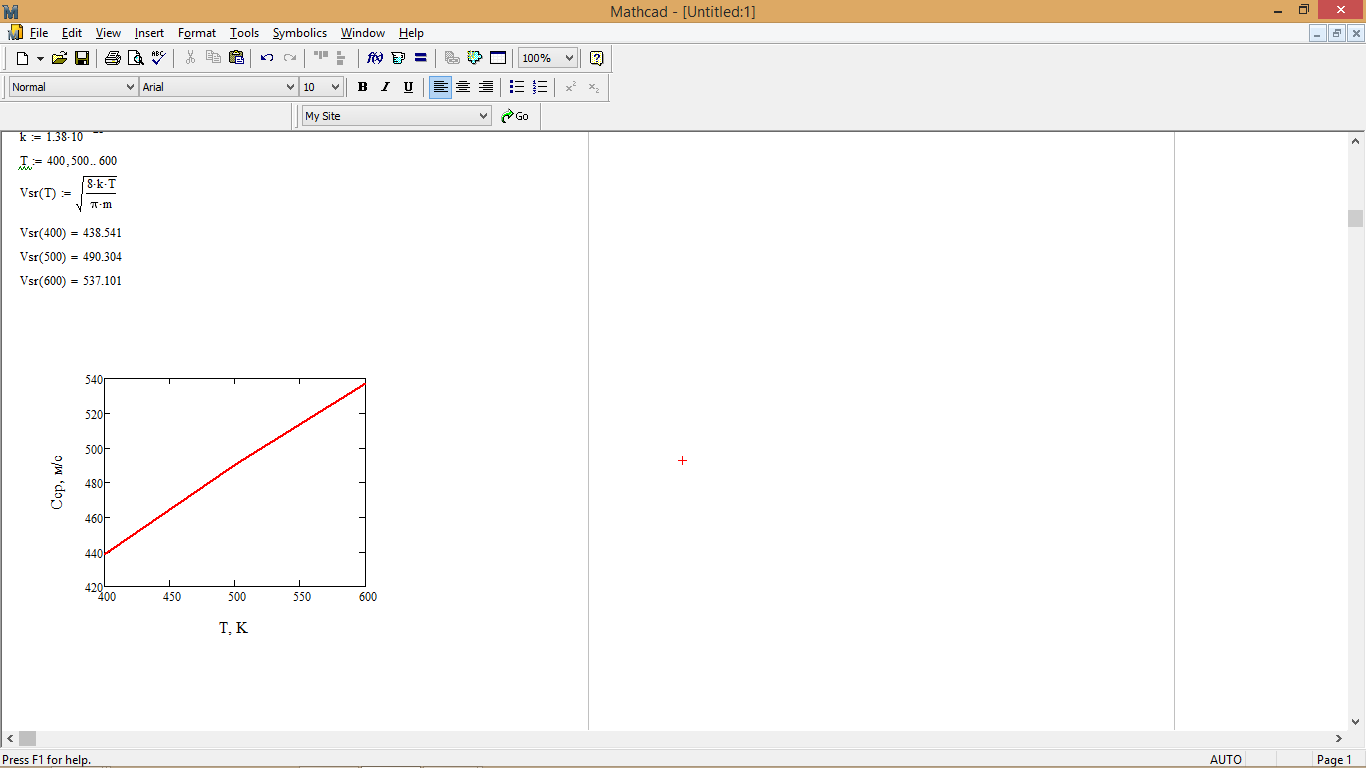
Рис. 1 – График зависимости средней скорости молекул CO₂ от температуры

1.1.2 Вычисление значений с_m

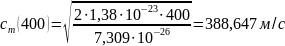
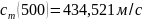
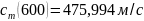
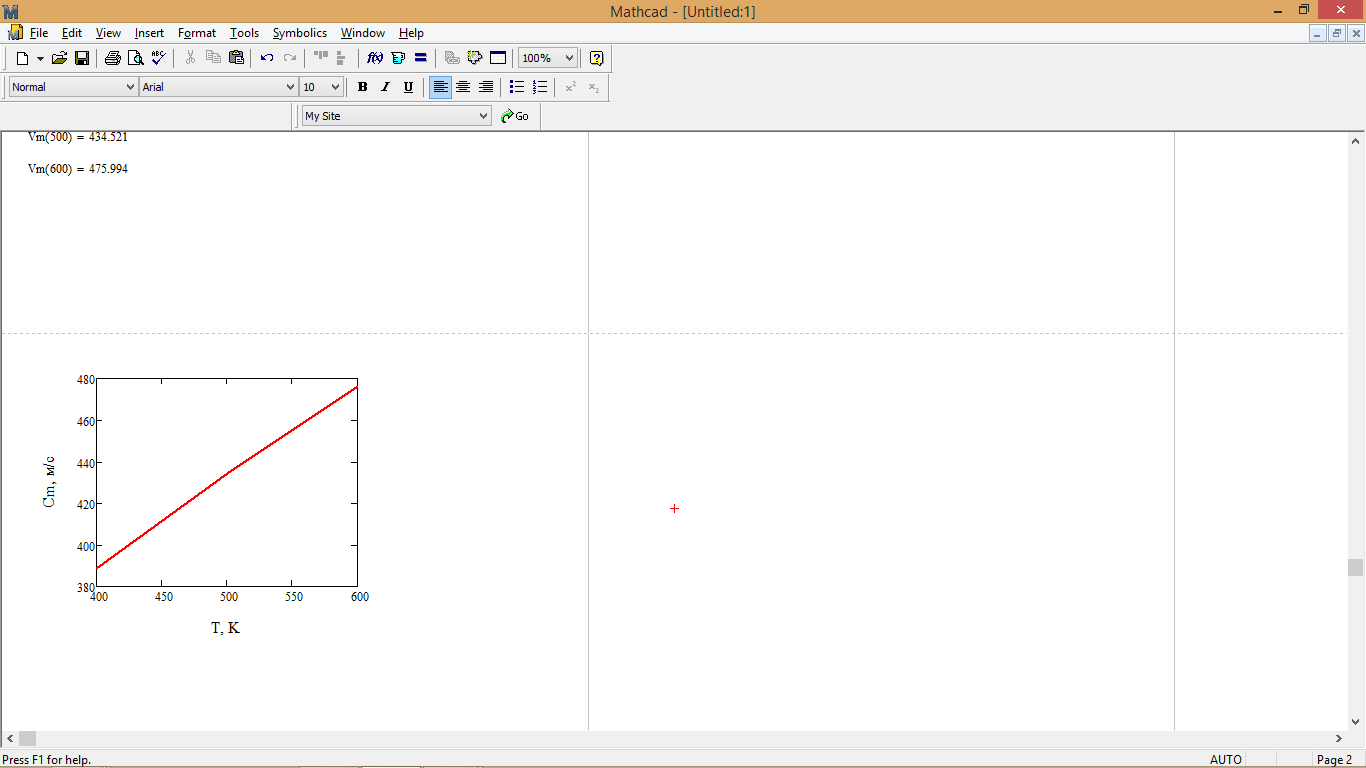
Рис. 2 – График зависимости наиболее вероятной скорости молекул CO₂ от температуры

1.1.3 Вычисление значений

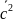
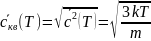
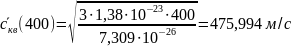
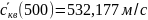
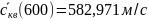
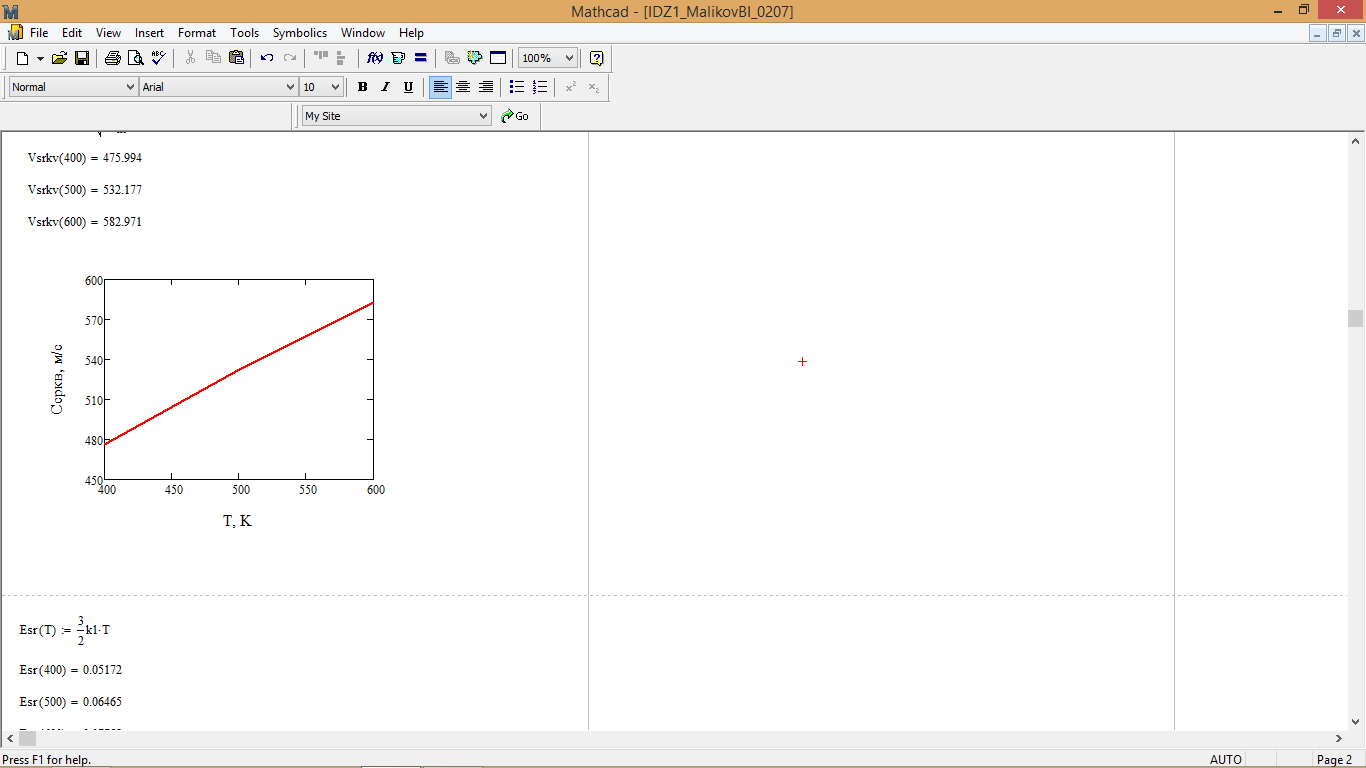
Рис. 3 – График зависимости среднеквадратичной скорости молекул CO₂ от температуры

1.1.4 Вычисление значений

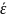
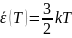
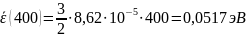
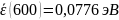
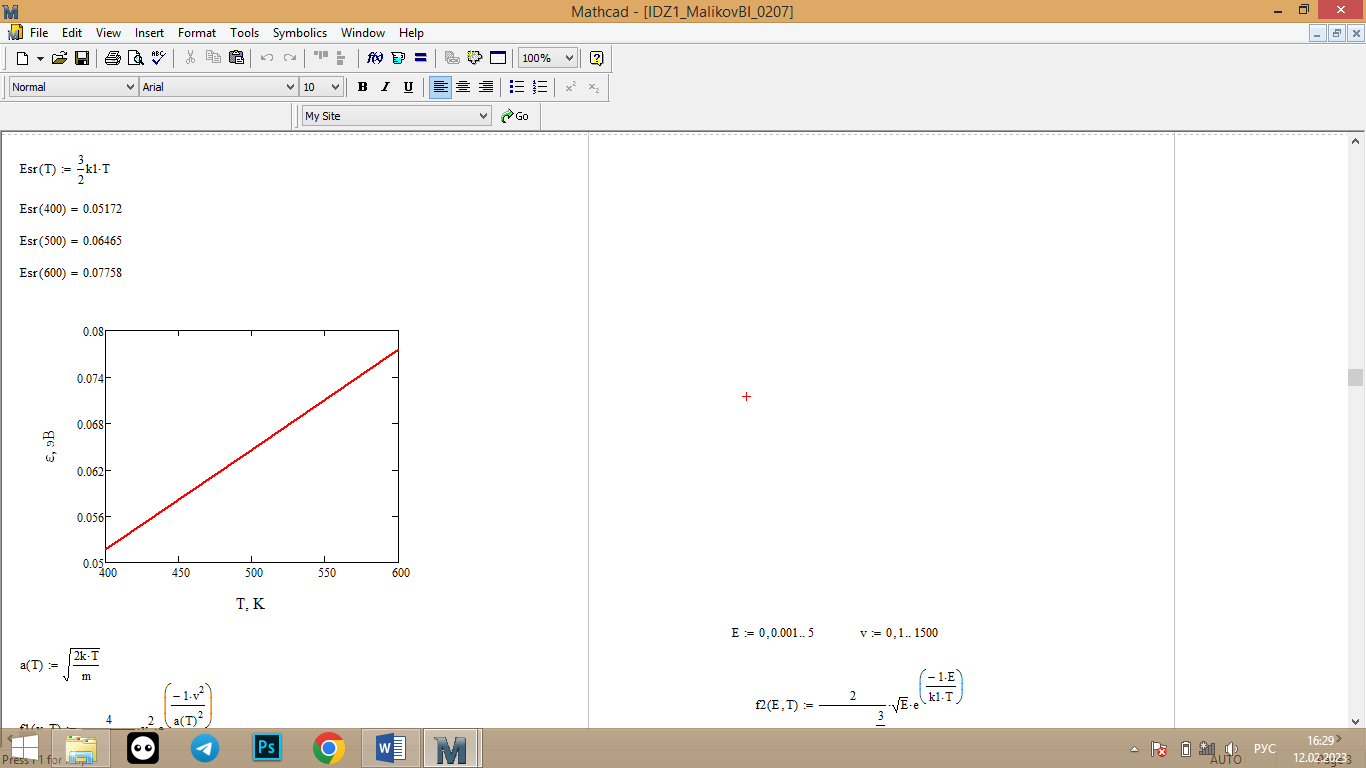
Рис. 4 – График зависимости средней энергии молекул CO₂ от температуры

1.2.1 Распределение Максвелла по абсолютным скоростям f(с)

f(c) =

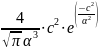
где:

α(T) =

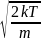
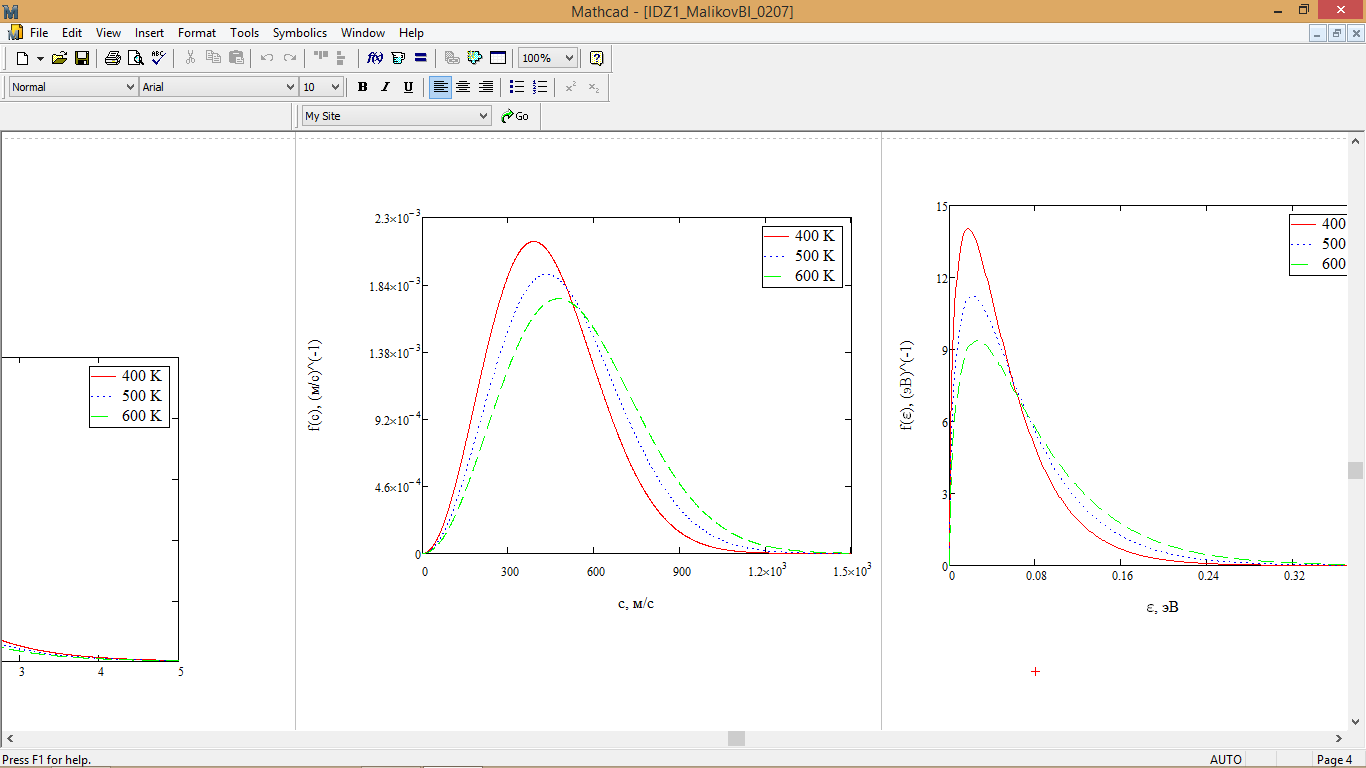
Рис. 5 – График распределения Максвелла по абсолютным скоростям

, c/м

, c/м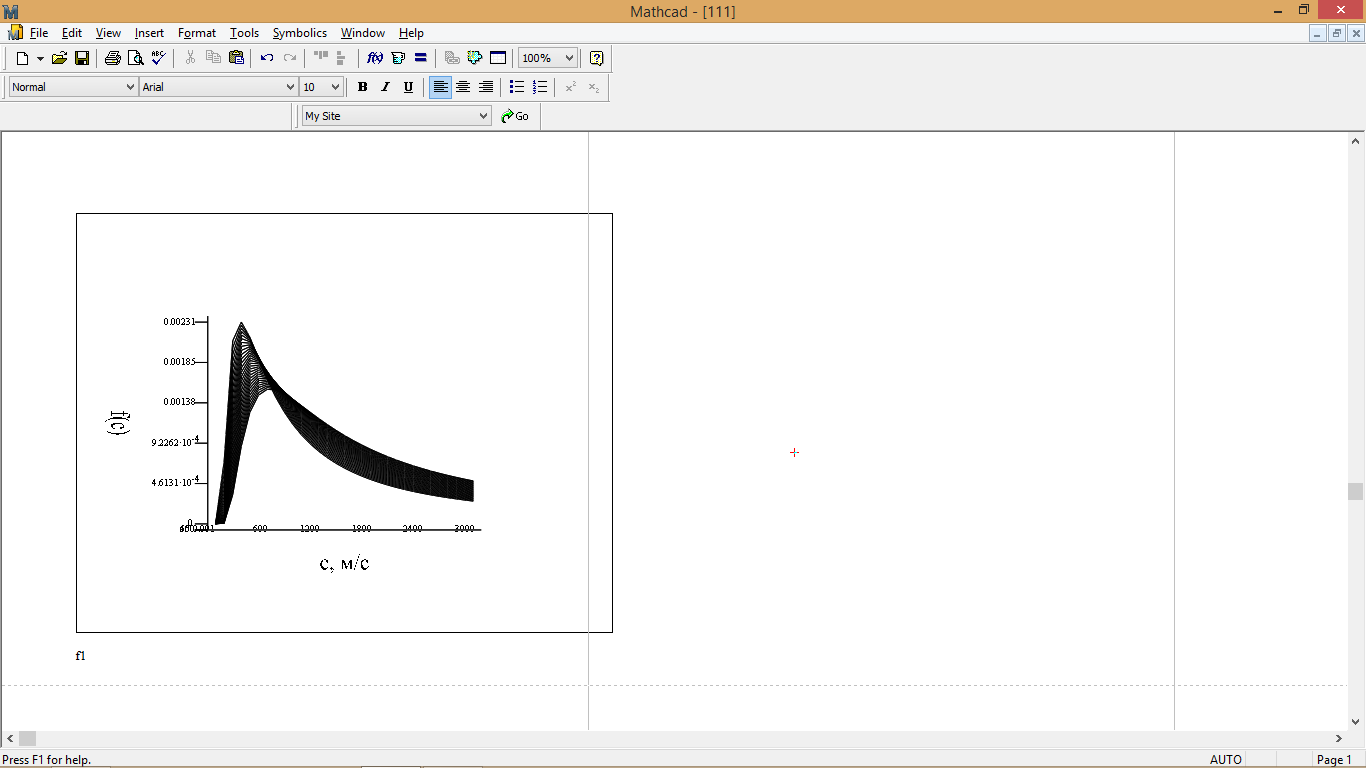

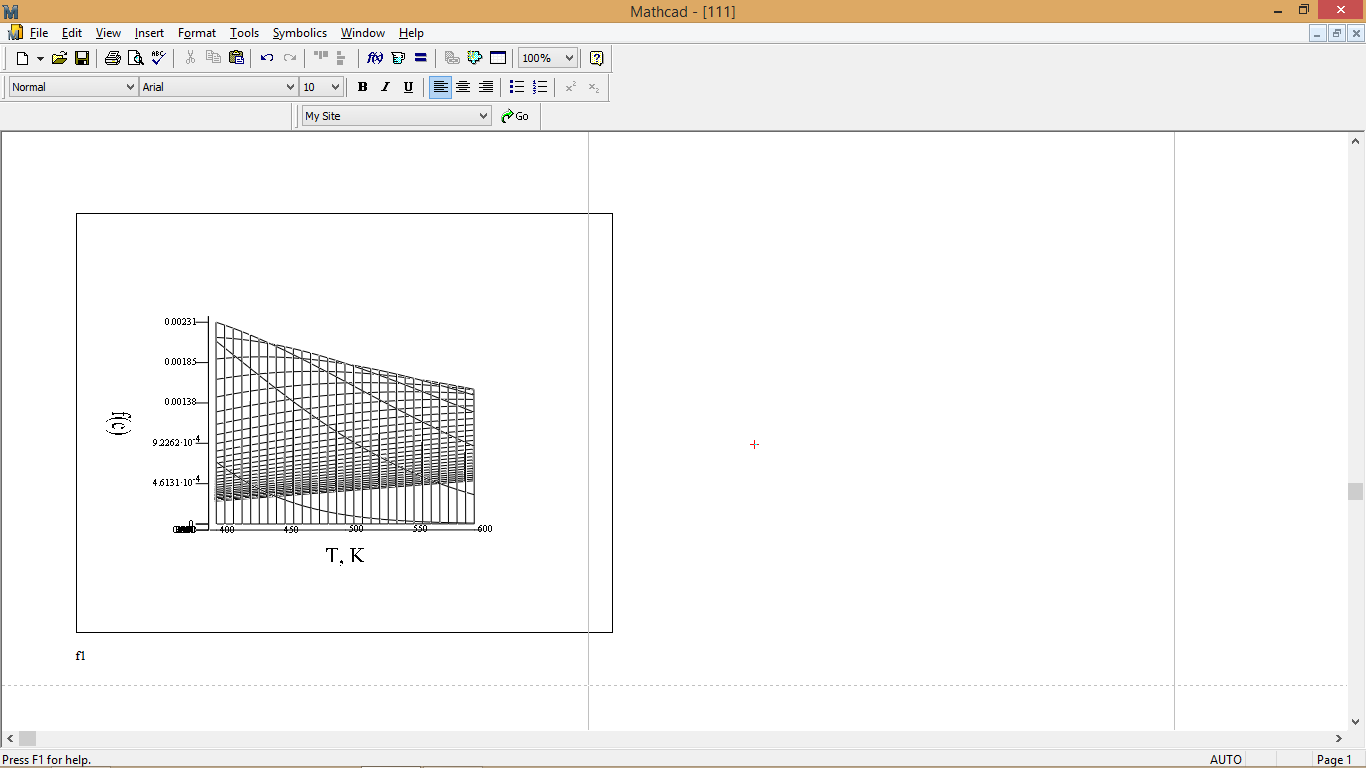
Рис. 6 – График распределения Максвелла по абсолютным скоростям в 3D-проекции на различные оси

, c/м

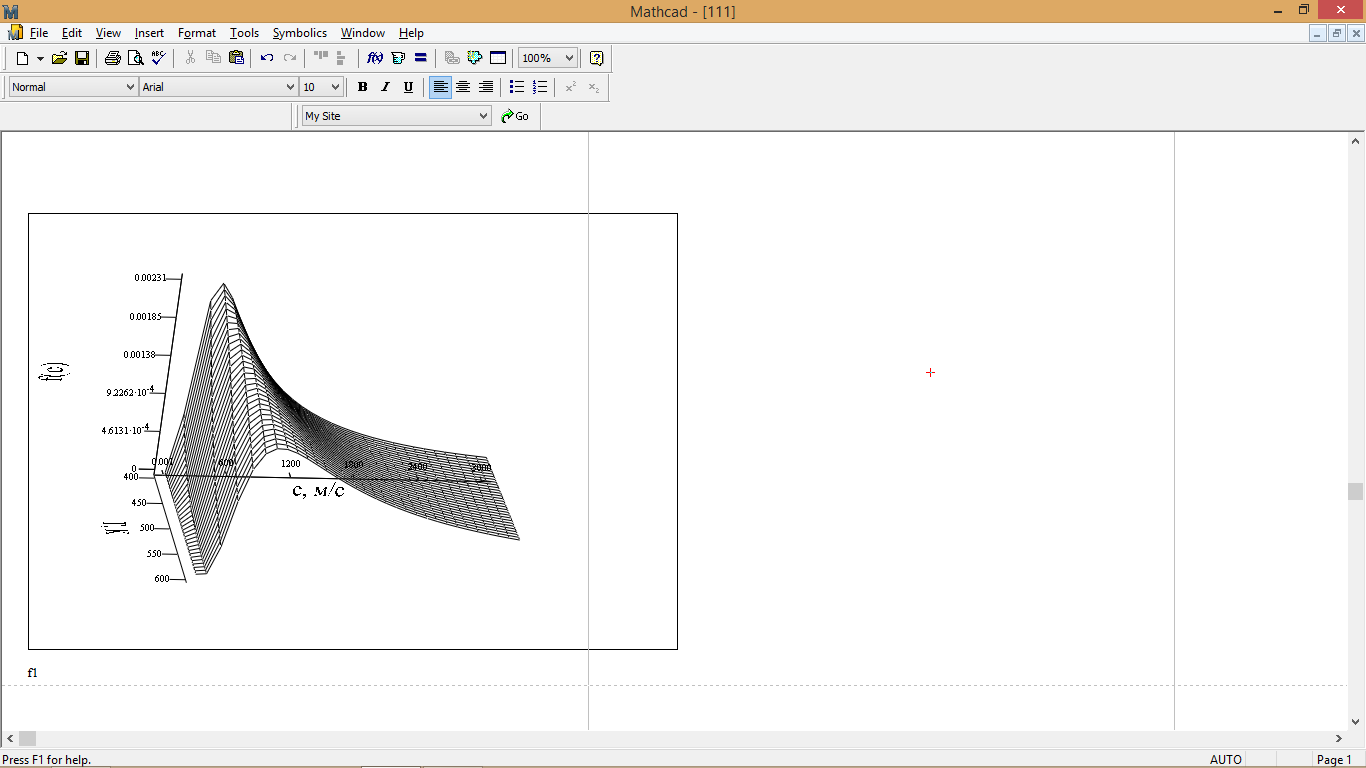
Рис. 7 – График распределения Максвелла по абсолютным скоростям в полной 3D-проекции

1.2.2 Распределение Максвелла по абсолютным энергиям f(ε)

f( ) =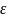

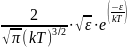
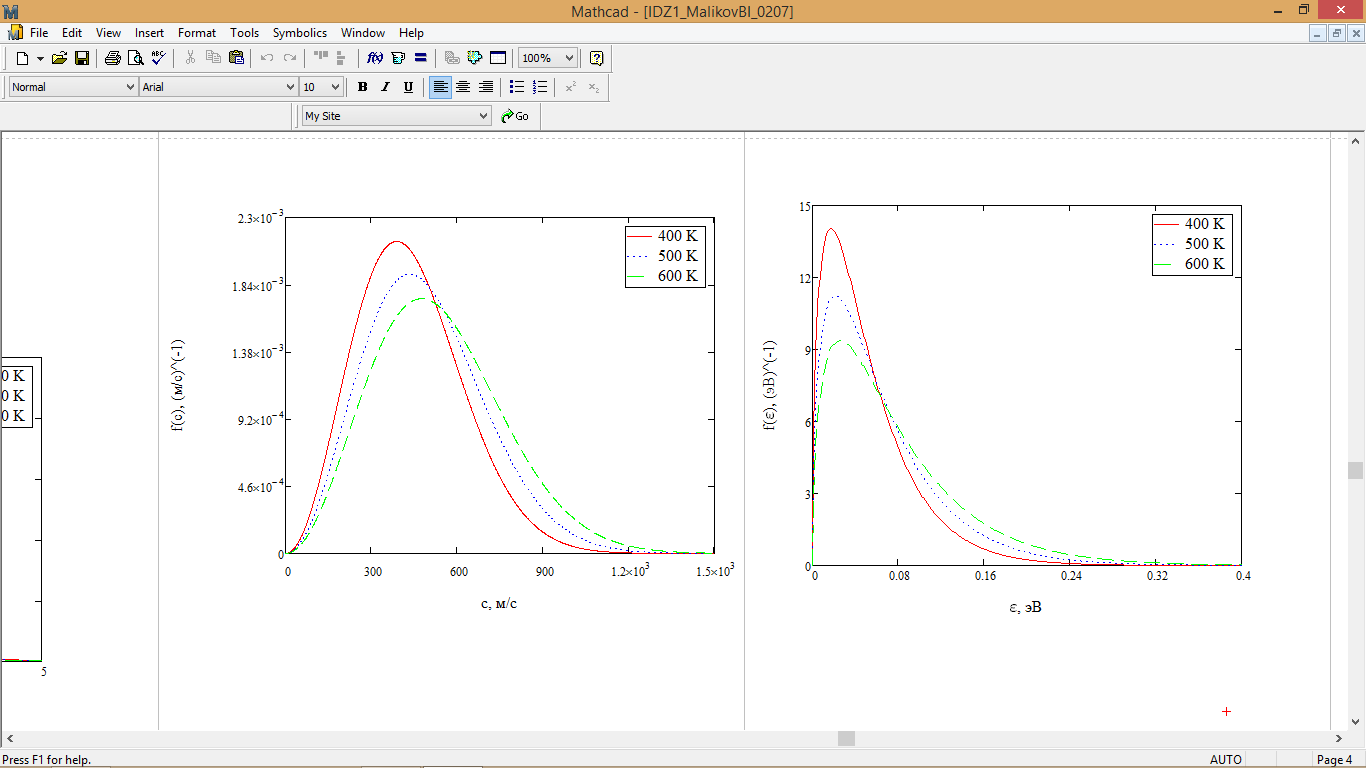
Рис. 8 – График распределения Максвелла по абсолютным энергиям

1.3.1 Распределение Максвелла по абсолютным скоростям f(с) в нормированных координатах

Нормирование координат проводим путем следующего преобразования для скоростей:

f(с∙

Для энергий:

f(ε∙

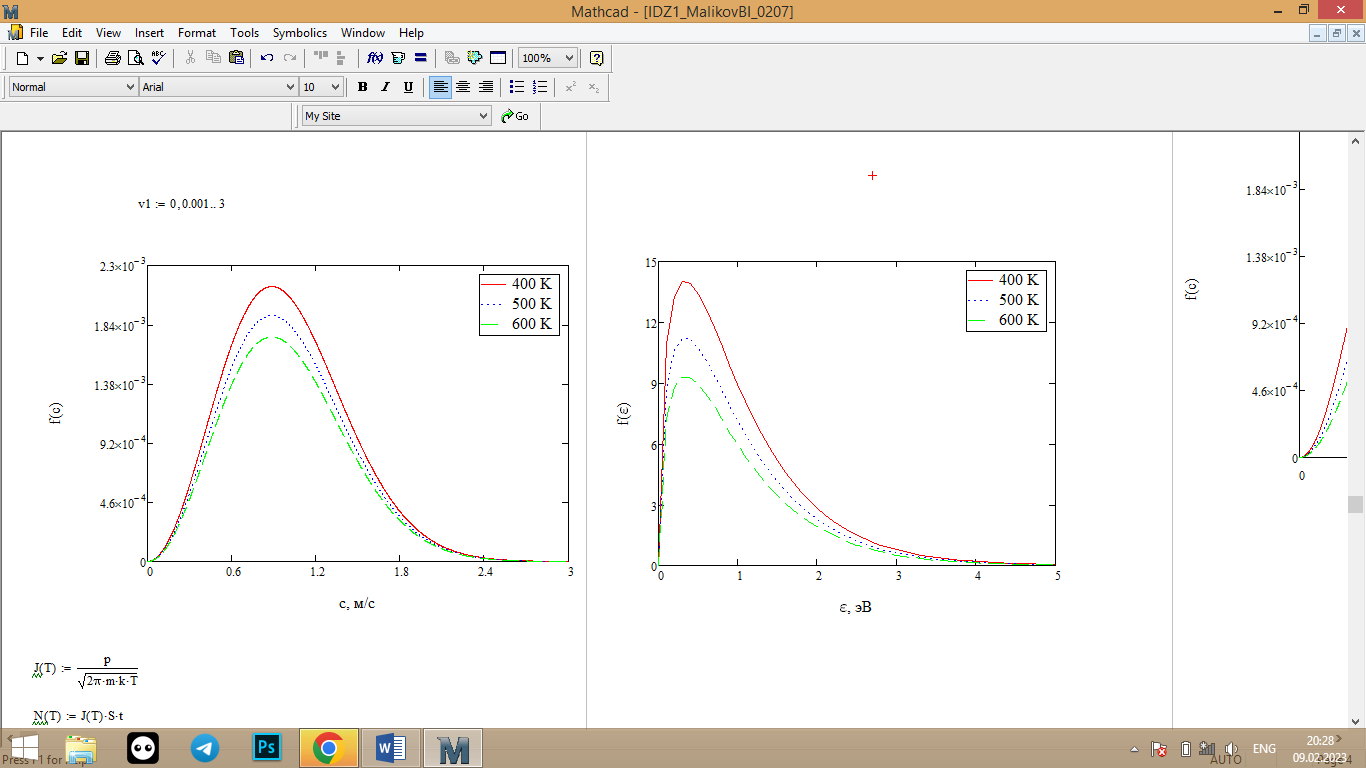
Рис. 9 – График распределения Максвелла по абсолютным скоростям в нормированных координатах

1.3.1 Распределение Максвелла по абсолютным энергиям f(ε) в нормированных координатах

Рис. 10 – График распределения Максвелла по абсолютным скоростям в нормированных координатах

2. Расчет числа частиц, которые при максимальной температуре (600 К) имеют скорости в диапазонах 1 м/c и 100 м/c в окрестностях ,

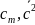
2.1.1 В диапазоне 1 м/с в окрестности

dN_с = N∙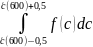

где N (при 600 К):

N = 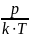= = 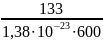1,6063∙10²² м^-3

тогда:

dN_с = N∙ = 2,714∙10¹⁹ м^-3

2.1.2 В диапазоне 100 м/с в окрестности

dN_с = N∙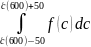

тогда:

dN_с = N∙ = 2,698∙10²¹ м^-3

2.2.1 В диапазоне 1 м/с в окрестности

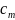
dN_с = N∙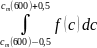

тогда:

dN_с = N∙ = 2,802∙10¹⁹ м^-3

2.2.2 В диапазоне 100 м/с в окрестности

dN_с = N∙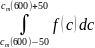

тогда:

dN_с = N∙ = 2,781∙10²¹ м^-3

2.3.1 В диапазоне 1 м/с в окрестности

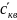
dN_с = N∙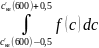

тогда:

dN_с = N∙ = 2,549∙10¹⁹ м^-3

2.3.2 В диапазоне 100 м/с в окрестности

dN_с = N∙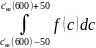

тогда:

dN_с = N∙ = 2,536∙10²¹ м^-3

3. Расчет числа частиц, которые при максимальной температуре (600 К) имеют энергию в диапазонах 1 мэВ и 30 мэВ в окрестности

3.1 В диапазоне 1 мэВ в окрестности

dN_ε = N∙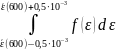

тогда:

dN_ε = N∙ = 9,577∙10¹⁹ м^-3

3.1 В диапазоне 100 мэВ в окрестности

dN_ε = N∙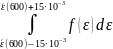

тогда:

dN_ε = N∙ = 2,882∙10²¹ м^-3

4. Зависимость числа соударений молекул газа с площадкой площадью 1 мм² за время 10 с

Плотность потока газа через поверхность:

J(T) =

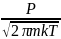
Отсюда, число соударений молекул газа с площадкой площадью 1 мм² (10^-6 м²) за время 10 с:

N(T) = J(T)∙S∙t

Вычисление числа соударений молекул газа с площадкой площадью 1 мм² (10^-6 м²) за время 10 с при разных температурах:

N(400) = 2,642∙10²⁴∙10^-6∙10 = 2,642∙10¹⁹

N(500) = 2,363∙10¹⁹

N(600) = 2,157∙10¹⁹

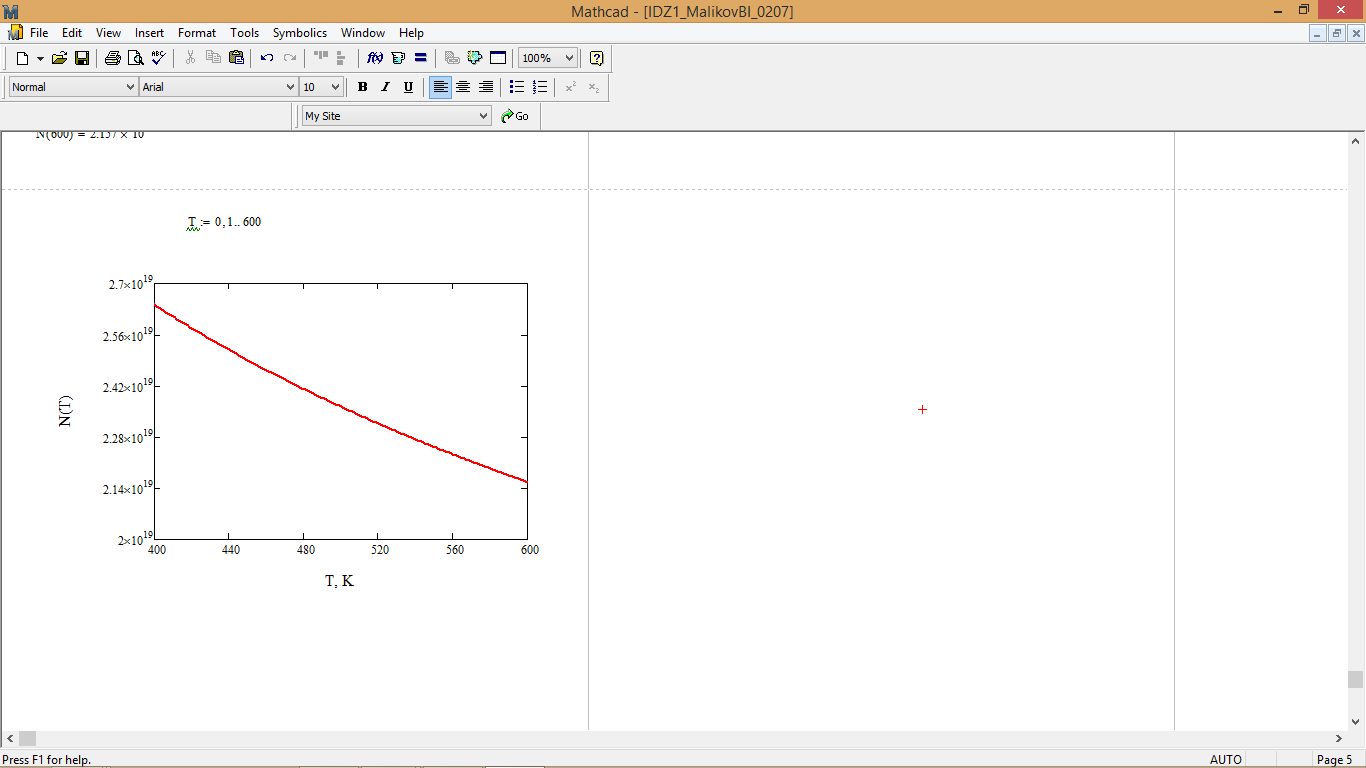
Рис. 11 – График зависимости числа соударений молекул газа с площадкой площадью 1 мм² за время 10 с от температуры