Лабы Яшкардин / Лаба 9 / ТОЭ Лаба 9 0207 Маликов Отчет

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра теоретических основ электротехники

отчет

по лабораторной работе №9

по дисциплине «Теоретические основы электротехники»

Тема: Исследование индуктивно связанных цепей

Студент гр. 0207		Маликов Б.И.
Преподаватель		Яшкардин Р.В.

Санкт-Петербург

2022

ЦЕЛЬ РАБОТЫ

Целью данной лабораторной работы является экспериментальное определение параметров двух индуктивно связанных катушек и проверка основных соотношений индуктивно связанных цепей при различных соединениях катушек.

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

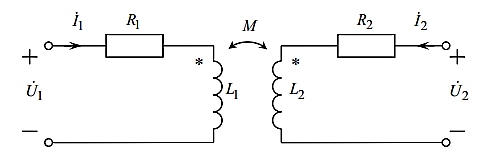
Рис. 1 - Схема замещения двух индуктивно связанных катушек, удовлетворительно учитывающая электромагнитные процессы в диапазоне низких и средних частот.

где L₁ и L₂ – индуктивности первой и второй катушек; R₁ и R₂ – сопротивления первой и второй катушек; М – взаимная индуктивность.

Важной величиной является коэффициент связи – степень магнитной связи двух катушек:

k = =

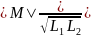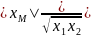
где x₁ = ωL₁ и x₂ = ωL₂ – индуктивные сопротивления катушек; x_M = M – сопротивление взаимной индуктивности; при этом 0  k  1.

В УГР уравнения цепи принимают вид:

Стоит отметить, что знак M и x_M определяется выбором положительных направлений токов I₁ и I₂. Для выбранных направлений токов M  0 , если включение катушек согласное, и M  0 , если включение встречное. Способ включения катушек устанавливается с помощью однополярных выводов, отмеченных «звездочками»: если токи катушек направлены одинаково относительно однополярных выводов, то катушки включены согласно; в противном случае включение встречное.

Параметры уравнения могут быть определены из двух опытов холостого хода, в одном из которых I₂  0 , в другом I₁  0 ; осуществляют эти опыты размыканием соответствующей пары внешних выводов катушек. Если используют катушки достаточно высокой добротности (ωL >> R ), то при определении индуктивностей допустимо пренебречь активными сопротивлениями обмоток катушек, т. е. считать R₁  0 и R₂  0 ; ошибка при этом будет несущественной с точки зрения инженерной практики. Полагая в уравнениях сначала I₂  0 , а затем I₂  0 , при условии R₁ = R₂ = 0 получаем соответственно:

Изобразим последовательное и параллельное соединение двух индуктивно связанных катушек:

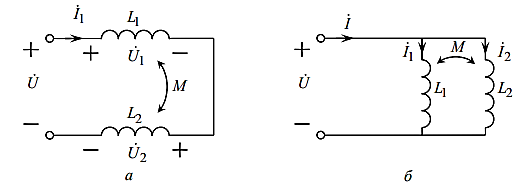
Рис. 2 - Последовательное и параллельное соединение двух индуктивно связанных катушек.

Для случая последовательного соединения двух индуктивно связанных катушек:

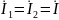
Решая систему уравнений при R_­1 = R₂ = 0 найдем выражение эквивалентной индуктивности:

L_Э = 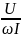= L₁ + L₂ + 2M

Для случая параллельного соединения двух индуктивно связанных катушек:

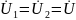
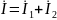
Решая систему уравнений при R_­1 = R₂ = 0 найдем выражение эквивалентной индуктивности:

L_Э = =

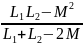
При этом M > 0 при согласном включении катушек, M < 0 при встречном.

Если к выводам второй катушки присоединить нагрузочное сопротивление Z_Н, получим двухобмоточный трансформатор – рис. 3. В трансформаторе энергия от источника, включенного в цепь первичной обмотки, передается нагрузке Z_Н, подключенной ко вторичной обмотке. Эта передача осуществляется без электрической связи между обмотками посредством изменяющегося потока взаимной индукции:

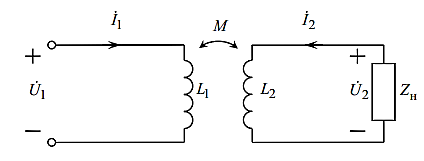
Рис. 3 – Схема двухобмоточного трансформатора.

Приняв 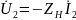и R₁ = R₂ = 0 в системе уравнений, получим:

H_U (jω) = =

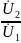В случае активной нагрузки Z_Н = R_Н модуль функции передачи по напряжению (АЧХ):

| H_U (jω)| =

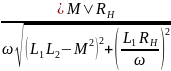
ПРОТОКОЛ НАБЛЮДЕНИЙ

ЛАБОРАТОРНАЯ РАБОТА №9

ИССЛЕДОВАНИЕ ИНДУКТИВНО СВЯЗАННЫХ ЦЕПЕЙ

Таблица 1

Номер катушки	Наблюдают				Вычисляют
	U1 , В	U2 , В	I , мА	x , Ом		L, Гн	|xM| , кОм	|M| , Гн
1
2

Таблица 2

Включение	Наблюдают					Вычисляют
	U, В	U1, В	U2, В	I, мА	I, мА		U1, В	U2, В	Lэ, Гн
Cогласное
Встречное

Таблица 3

Включение	Наблюдают		Вычисляют
	U, В	I, мА	I, мА	Lэ, Гн
Согласное
Встречное

Таблица 4

Частота	Нагрузка R=100 Ом
f, Гц	U1 , В	U2 , В	|Hu(jw)| = U2/U1		U1 , В		U2 , В		|Hu(jw)| = U2/U1
			Опыт	Расчёт					Опыт	Расчет

Выполнили: Маликов Б.И.

Бурчик Н.Е.

Группа № 0207

Преподаватель: Яшкардин Р.В.

Дата: