МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра теоретических основ электротехники

отчет

по лабораторной работе №7

по дисциплине «Теоретические основы электротехники»

Тема: Исследование резонансных явлений в простых электрических цепях

Студент гр. 0207		Маликов Б.И.
Преподаватель		Яшкардин Р.В.

Санкт-Петербург

2022

ЦЕЛЬ РАБОТЫ

Целью данной лабораторной работы является исследование резонанса и АЧХ последовательного и параллельного колебательных контуров.

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

Прежде всего, следует дать определение понятию резонанс: резонанс – состояние электрической цепи в УГР, при котором фаза тока и напряжений на входе совпадают.

Различают два вида резонанса – резонанс напряжений и резонанс токов. Изобразим каждый из приведенных примеров:

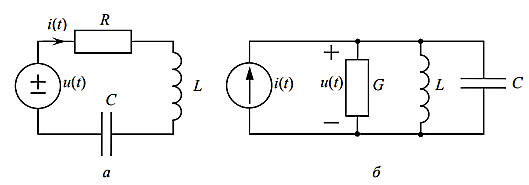
Рис. 1 – Резонанс напряжений, последовательный контур (а) и резонанс токов, параллельный контур (б).

Определим комплексное сопротивление последовательного контура:

Z (jω) = R +

Определим комплексную проводимость параллельного контура:

Y (jω) = G +

Найдем резонансную частоту ω₀:

ω₀ = , а f₀ =

При резонансе напряжений модуль комплексной проводимости максимальный, то есть ток при резонансе напряжений (ω = ω₀) достигает максимальных значений:

|Y| = = =

при этом, ток:

I₀ =

Напряжения на емкости и индуктивности в последовательной цепи на рис.1, а, при резонансе компенсируют друг друга и могут быть во много раз больше напряжения источника. При этом, отношение действующего значения напряжения любого из реактивных элементов к напряжению источника при   ₀ называют добротностью Q последовательного контура:

Q = = = = = =

где  - характеристическое сопротивление контура.

Определим индуктивность и емкость:

L =

C =

При резонансе токов модуль комплексного сопротивления максимальный, то есть напряжение при резонансе токов (ω = ω₀) достигает максимальных значений:

|Z| = = =

при этом, напряжение:

U₀ =

Токи, протекающие через индуктивность и емкость параллельной цепи на рис. 1, б, при резонансе компенсируют друг друга и могут во много раз быть больше тока источника. Отношение действующего значения тока любого из реактивных элементов к току источника при   ₀ называют добротностью параллельного контура:

Q = = = = = =

В случае отклонения частоты от резонансной реактивное сопротивление последовательного контура и реактивная проводимость параллельного контура не равны нулю, поэтому ток первого и напряжение второго уменьшаются.

Стоить заметить, что АЧХ последовательного контура – зависимость модуля проводимости от частоты:

|Y (jω)| = =

При этом, АЧХ параллельного контура – зависимость модуля сопротивления от частоты:

|Z (jω)| = =

По резонансной кривой можно определить добротность контура. Она равна отношению f₀ к полосе пропускания f , измеренной по уровню 0,707 от максимума резонансной кривой:

Q =

Рис. 2 – Вид резонансной кривой при разных значениях Q, R и f.

Обработка результатов измерений

1. Экспериментальное исследование резонанса напряжений.

1.1 Исследование резонанса напряжений и ачх контура с малыми потерями.

Рис. 3. Схема исследования резонанса напряжений и АЧХ с малыми потерями.

Вычисление значений R, Q, , L и C:

R = = = 138,41 [Ом]

Q = = = 22,35

 = QR = 22,35∙138,41 = 3093,49 [Ом]

L = = = 0,14 [Гн]

C = = = 1,43∙10^-2 [мкФ]

Таблица 1

Исследование резонанса напряжений контура с малыми потерями.

Измерения при резонансе				Вычисляют
U , В	I0 , мА	f0 , кГц	UС0 , В		R , Ом	Q	 , Ом	L , Гн	C , мкФ
2	14,45	3,6	44,7		138,41	22,35	3093,49	0,14	1,43∙10-2

Модуль проводимости вычисляется по формуле:

|Y (jω)| = =

ω = 2πf

Пример вычислений при частоте f = 1,8 [кГц]:

Практика:

|Y (jω)| = = = 0,23∙10^-3 [См]

Теория:

ω = 2π∙1,8∙10³ = 11309,73

|Y (jω)| = = 0,22∙10^-3 [См]

Таблица 2

Исследование ачх контура с малыми потерями.

Измеряют				Вычисляют
f , кГц	I , мА	|Y (j)| , См	ω , рад/c		|Y (j)| , См
1,8	0,46	0,23∙10-3	11309,73		0,22∙10-3
2	0,54	0,27∙10-3	12566,37		0,26∙10-3
2,5	0,8	0,40∙10-3	15707,96		0,44∙10-3
2,9	1,61	0,81∙10-3	18221,24		0,77∙10-3
3,3	2,75	1,38∙10-3	20734,51		2,04∙10-3
3,6	14,45	7,23∙10-3	22619,47		6,35∙10-3
4,1	4,57	2,29∙10-3	25761,06		1,11∙10-3
5,3	1,08	0,54∙10-3	33300,88		0,39∙10-3
6,2	0,72	0,36∙10-3	38955,75		0,27∙10-3
6,9	0,59	0,30∙10-3	43353,98		0,22∙10-3
7,2	0,56	0,28∙10-3	45238,93		0,21∙10-3

Вывод: исключая инструментальную погрешность, практические вычисления совпадают с теоретическими.

Рис. 4. АЧХ контура с малыми потерями.

По АЧХ контура с малыми потерями вычислим добротность:

Q =

где △f – полоса пропускания, , измеренная по уровню 0,707 от максимума АЧХ.

0,707∙6,35∙10^-3 = 4,49∙10^-3 [См] => △f = 3,8 – 3,4 = 0,4 [кГц] => Q = = 9

Сравним с теоретическими значениями:

Теория: Q = = = 22,35

Практика: Q = = 9

Значения не совпадают, что можно объяснить малым диапазоном частот, в котором проводились измерения, а также инструментальной погрешностью.