МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра теоретических основ электротехники

отчет

по лабораторной работе №3

по дисциплине «Теоретические основы электротехники»

Тема: Исследование свободных процессов в электрических цепях

Студент гр. 0207		Маликов Б.И.
Преподаватель		Яшкардин Р.В.

Санкт-Петербург

2022

ЦЕЛЬ РАБОТЫ

Целью данной лабораторной работы является изучение связи между видом свободного процесса в электрической цепи и расположением ее собственных частот (корней характеристического уравнения) на комплексной плоскости, так же целью данной работы является экспериментальное определение собственных частот и добротности RLC-контура по осциллограммам.

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

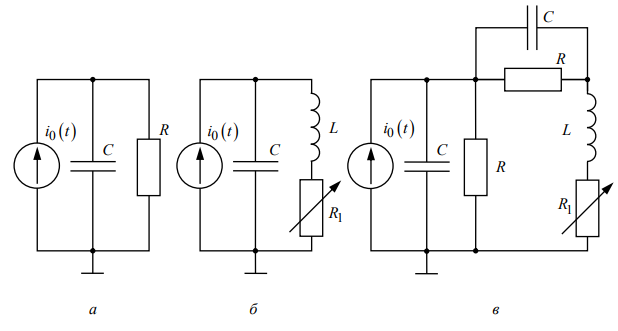
Рис. 1 – Схемы цепей, представленные в данной работе

Задачей выполнения данной лабораторной работы является изучения свободных процессов в цепях, схемы которых изображены на рис. 1. Как можно заметить, в каждой из цепей содержится источник импульсов тока i₀(t), заряжающих конденсатор C. Стоит уточнить, что разрядка конденсатора происходит в паузах между импульсами, и тогда цепь находится в свободном режиме, так как в момент пауз i₀ = 0 (т.е отсутствуют какие-либо импульсы). Так же, для изучения свободных процессов в данных цепях используется осциллограф, при этом, исследуется осциллограмма напряжения на выводах элементов.

Система линейных дифференциальных уравнений служит для описания поведения линейных цепей. Стоит заметить, что вид свободного процесса в цепи напрямую зависит от собственных частот цепи – p_k (корней характеристического уравнения).

Собственные частоты цепи рассчитываются путем приравнивания входной проводимости к нулю, то есть находятся путем решения уравнения: Y(p) = 0.

Приведем примеры:

Порядок в цепи зависит от количества L и C элементов.

1) Так, схема рис. 1, а, относится к цепи первого порядка. Тогда, входная проводимость:

Y(p) = pC +

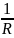
Приравняем к нулю и получим p₁:

pC + = 0 => p₁ = - a = -

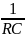
2) Схема рис. 1, б, относится к цепи второго порядка. Тогда, данная цепь будет обладать двумя собственными частотами (p₁ и p₂). Найдем данные значения.

Входная проводимость: Y(p) = pC +

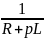
Приравнивая к нулю, получим: pC + = 0 =>

=> p_1,2 = - 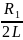± 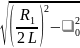, где a = , =

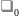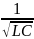
3) Схема рис. 1, в, соответствует цепи третьего порядка. Найдем входную проводимость, приравняем к нулю и найдем собственные частоты цепи (p₁, p₂ и p₃).

Входная проводимость: Y(p) = pC + +

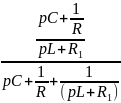
Приравняем к нулю: pC + + = 0 => p₁ = - a = - ,

p_2,3 = - 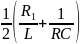± 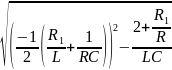, где a =

Для цепи первого порядка (рис. 1, а) свободный процесс описывается так:

То есть, как можно заметить, свободный процесс описывается затухающей экспонентой. При этом, описание свободного процесса в цепи 1-го порядка может быть получено и без составления системы диф. уравнений цепи. Для этого достаточно найти τ – постоянную времени.

Так же, в данном уравнении: u – напряжение на каком-либо элементе цепи, t – время; α – постоянная затухания и A – постоянная интегрирования.

Перейдем к рассмотрению цепи второго порядка. В данном случае, имеются два значения собственных частот: p₁ и p₂. Собственные частоты могут быть как вещественными, так и комплексно-сопряженными. Если рассматривается случай простых вещественных частот, то:

p₁ = -a₁ и p₂ = -a₂

Тогда, в этом случае, свободный процесс описывается следующим образом:

При этом, такой свободный процесс называется апериодическим, так как в описании процесса отсутствуют sin или cos.

Изобразим временную диаграмму для свободного процесса в цепи первого порядка (рис. 2, а) и для свободного процесса второго порядка (рис. 2, б):

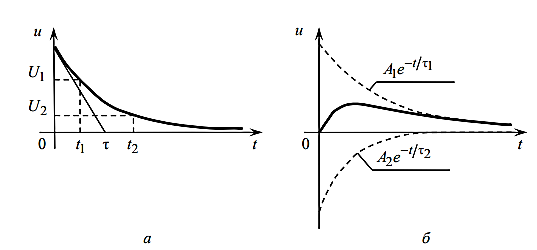
Рис.2 – Временные диаграммы свободных процессов

Так же, рассмотрим случай комплексно-сопряженных собственных частот:

p_1,2 = -a ± j

Тогда, свободный процесс:

В данном случае, свободный процесс является колебательным, так как в его описании содержится cos.

Если же рассматривать вещественные кратные собственные частоты, получим:

p₁ = p₂ = -a

Свободный процесс в этом случае:

Изобразим временную диаграмму для данных процессов:

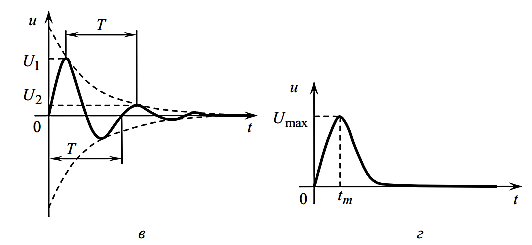
Рис. 3 – Временные диаграммы свободных процессов в случае a -комплексно-сопряженных собственных частот и б - вещественных кратных собственных частот

Стоит заметить, что постоянную затухания можно найти следующим образом (рис. 2, а):

a =

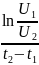
Так же, можно найти 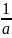 = , проведя касательную, как изображено на рис. 2, а.

При этом, собственная частота цепи:

p = -a = -

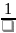
В случае рис. 3, в, собственные частоты:

p_1,2 = -a ± j = -a ± j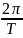

В случае рис. 3, г, собственные частоты цепи:

p₁ = p₂ = -a = -

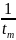
Определимся с добротностью последовательного RLC - контура:

Q = 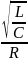= = 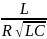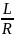₀ =

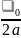
При этом, ₀ = - частота незатухающих колебаний в идеальном контуре.

Также, собственные частоты последовательного RLC - контура можно записать следующим образом:

p_1,2 = -

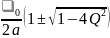
Стоит заметить, что при Q < 0,5 - апериодический режим, Q = 0,5 – критический режим, Q > 0,5 – колебательный режим, а Q → ∞ – незатухающий колебательный режим.

При Q > 10 с высокой степенью точности можно считать:

p_1,2 = -

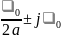
Тогда, формула добротности:

Q = = =

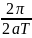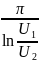
Учитывая отношение напряжений за n периодов колебаний:

Q = = =

Обработка результатов измерений

1. Исследование свободных процессов в цепи первого порядка.

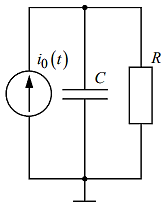
Рис. 1 – Схема цепи первого порядка

C = 0,02 [мкФ], R = 5 [кОм], T_c = 1,2 [мс], источником тока i₀(t является генератор импульсов:

Рис. 2 – Выставленные параметры осциллографа.

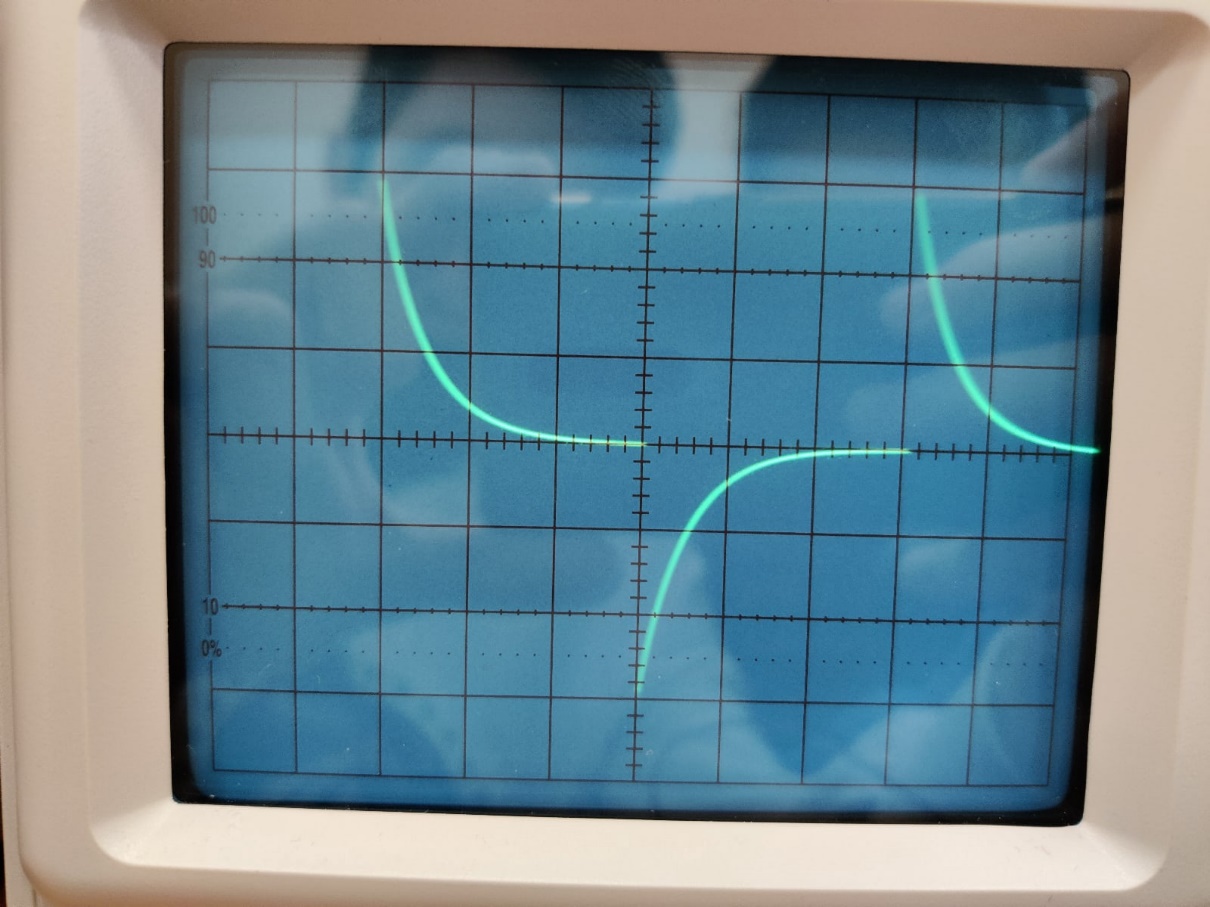
Рис. 3 – Осциллограмма при исследовании свободных процессов в цепи первого порядка.

Вычислим собственную частоту цепи теоретически:

p = 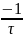= = 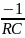= 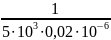-10000

Определим собственную частоту цепи по осциллограмме:

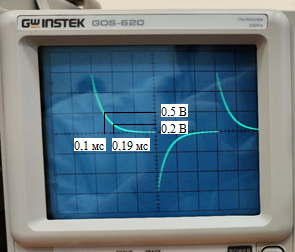
Рис. 4 – Определение собственой частоты при исследовании свободных процессов в цепи первого порядка.

p = -α = - 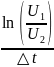= - = -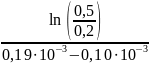10181

Таким образом, теоретически рассчитанная собственная частота цепи приблизительно равна собственной частоте цепи, найденной по осциллограмме.

Определим свободный процесс

U_C(t) = Ae^-10000t

Отобразим диаграмму расположения собственных частот на комплексной плоскости:

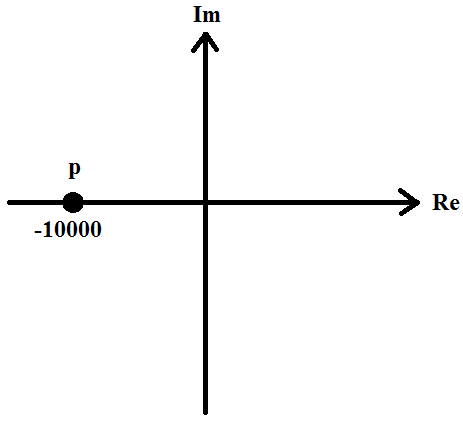
Рис. 5 - Диаграмма расположения собственных частот при исследовании свободных процессов в цепи первого порядка на комплексной плоскости.

Ответы на вопросы

1. Каким аналитическим выражением описывается осциллографируемый процесс?

Ответ:

Осциллографируемый процесс описывается выражением U_C(t) = Ae^-10000t

2. Соответствует ли найденная собственная частота теоретическому расчету, выполненному согласно (3.1)?

Ответ:

Найденная собственная частота приблизительно равна частоте, найденной теоретически, а именно, теоретически получили: p = -10000, практически: p = -10181.

2. Исследование свободных процессов в цепи второго порядка

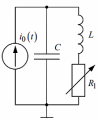
Рис. 6 – Схема цепи второго порядка.

С = 0,02 [мкФ], L = 25 [мГн], R₁ изменяется в зависимости от эксперимента.

2.1. Снятие осциллограммы процесса при R₁ = 0,5 [кОм] (колебательный режим):

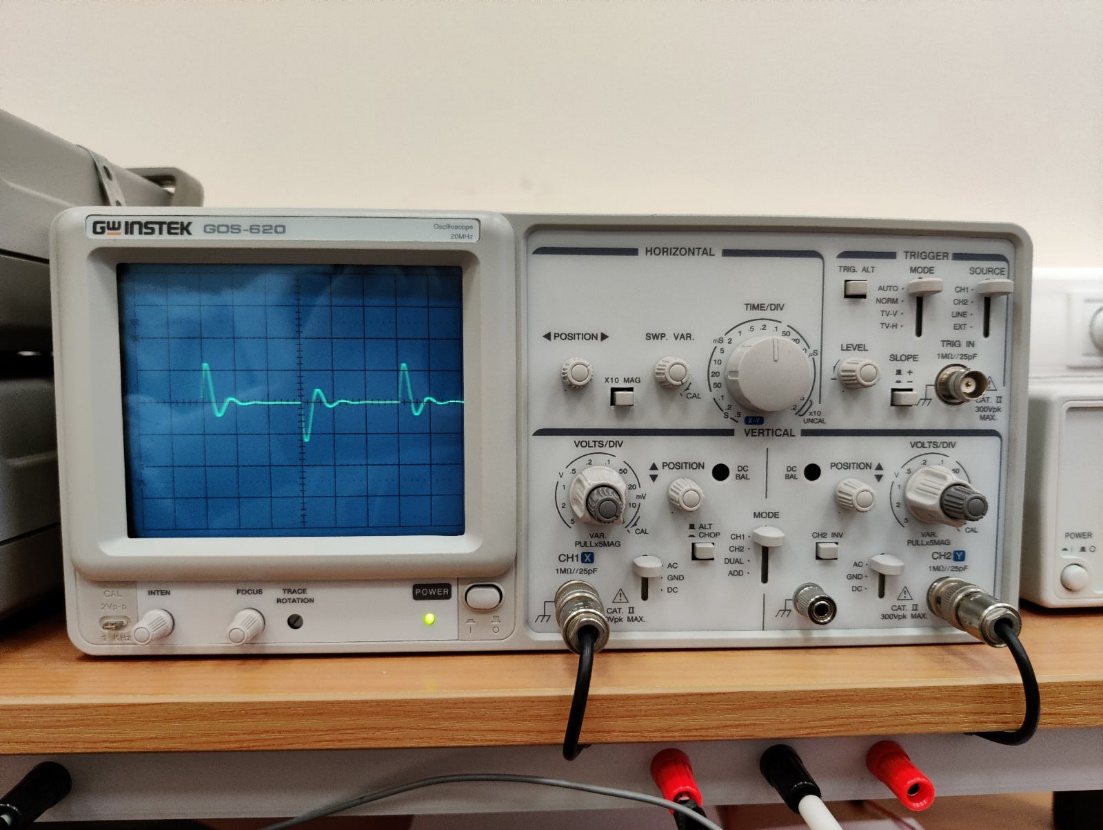
Рис. 7 – Осциллограмма при исследование свободных процессов в цепи второго порядка (R­₁ = 0,5 [кОм]).

Вычислим собственные частоты цепи теоретически:

p_1,2 = ± 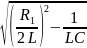= 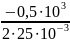± 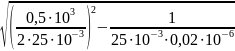= -10000 ± j∙43589

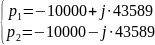
Вычислим собственные частоты цепи по осциллограмме:

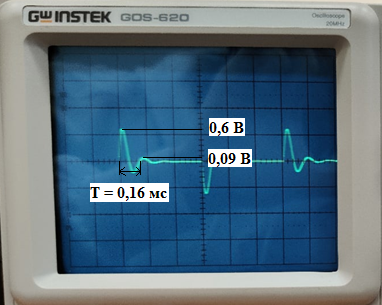
Рис. 8 - Определение собственой частоты при исследовании свободных процессов в цепи второго порядка (R­₁ = 0,5 [кОм]).

α = , где △t = T, тогда, получим:

α = 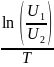= = 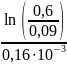11857

p_1,2 = -a ± j = -a ± j = -11857 ± j∙39250

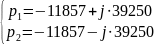
Таким образом, теоретически рассчитанные собственные частоты цепи приблизительно равны собственным частотам цепи, найденным по осциллограмме.

Определим свободный процесс:

U_R(t) = A₁e^-10000tcos(43589t) + A₂ e^-10000tsin(43589t)

Отобразим диаграмму расположения собственных частот на комплексной плоскости:

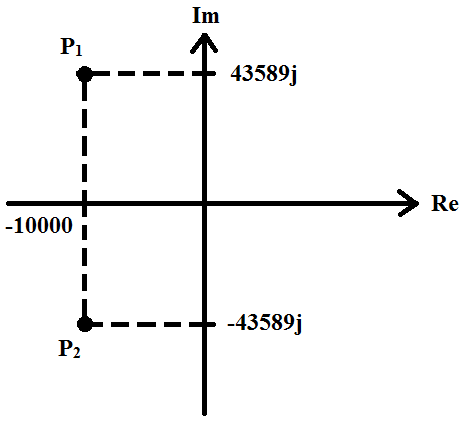
Рис. 9 - Диаграмма расположения собственных частот при исследовании свободных процессов в цепи второго порядка на комплексной плоскости

(R­₁ = 0,5 [кОм]).

Вычислим добротность контура теоретически:

Q = =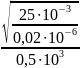 = 2,24

Вычислим добротность контура по осциллограмме:

Q = = = = 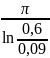= 1,66, добротность соответствует колебательному режиму (Q > 0,5).

2.2. Снятие осциллограммы процесса при R₁ = 3 [кОм] (апериодический режим):

Рис. 10 – Осциллограмма при исследование свободных процессов в цепи второго порядка (R­₁ = 3 [кОм]).

Вычислим собственные частоты цепи теоретически:

p_1,2 = ± = ±

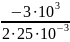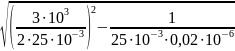
= - 60000 ± 40000

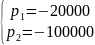
Вычислим собственные частоты цепи по осциллограмме:

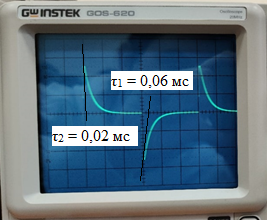
Рис. 11 - Определение собственой частоты при исследовании свободных процессов в цепи второго порядка (R­₁ = 3 [кОм]).

p₁ = - 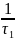= - = -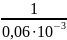16667

p₂ = - 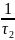= - = -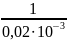50000

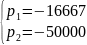
Определим свободный процесс:

U_R(t) = A₁e^-20000t + A₂e^-100000t

Отобразим диаграмму расположения собственных частот на комплексной плоскости:

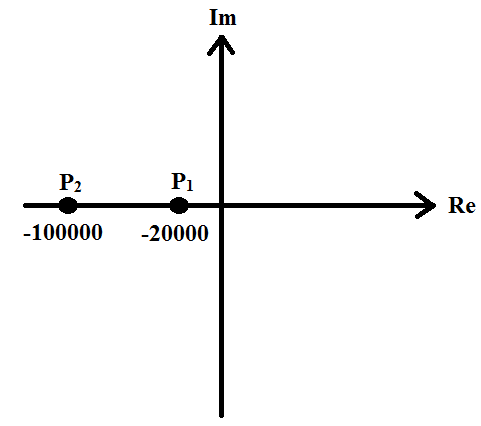
Рис. 12 - Диаграмма расположения собственных частот при исследовании свободных процессов в цепи второго порядка на комплексной плоскости

(R­₁ = 3 [кОм]).

2.3. Снятие осциллограммы процесса при R₁ = R_КР = 1,6 [кОм] (критический режим):

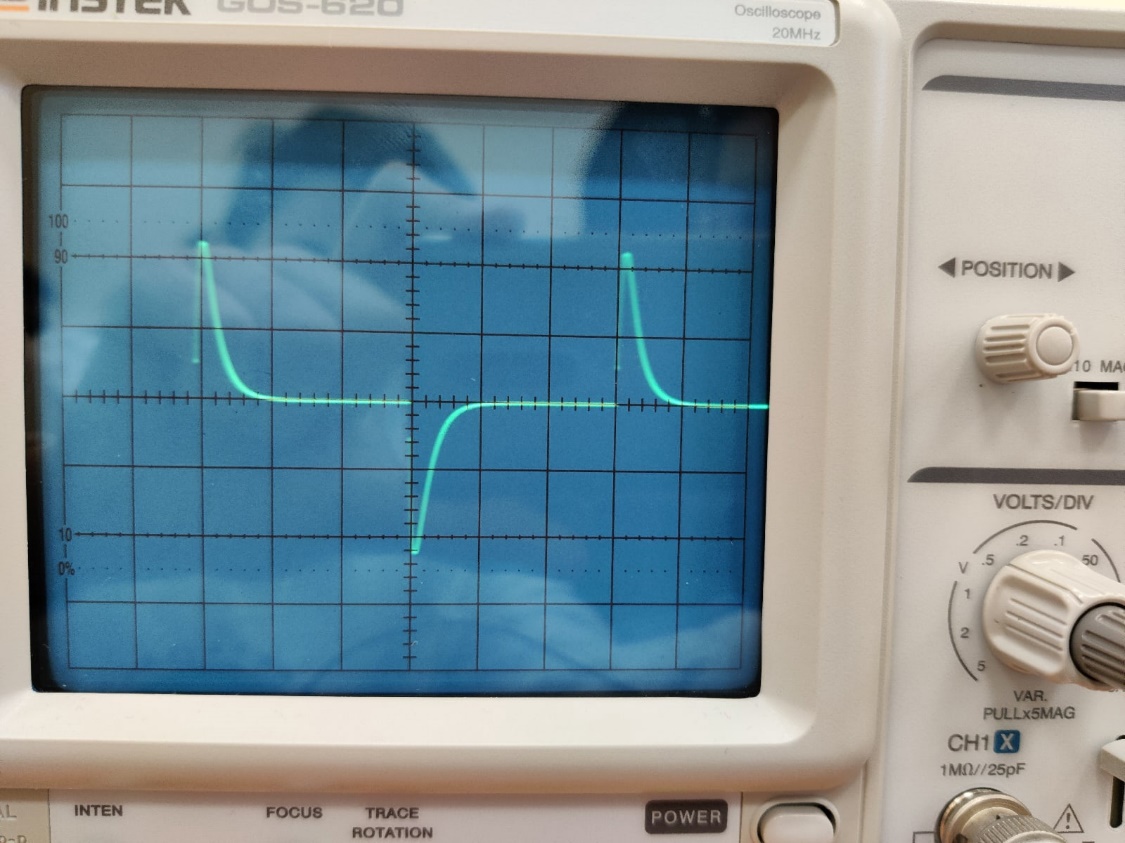
Рис. 13 – Осциллограмма при исследование свободных процессов в цепи второго порядка (R­₁ = R_КР = 1,6 [кОм]).

Вычислим собственные частоты цепи теоретически:

p₁ = p₂ = - α = 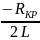= = 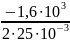-3,2∙10⁴

Вычислим собственные частоты цепи по осциллограмме:

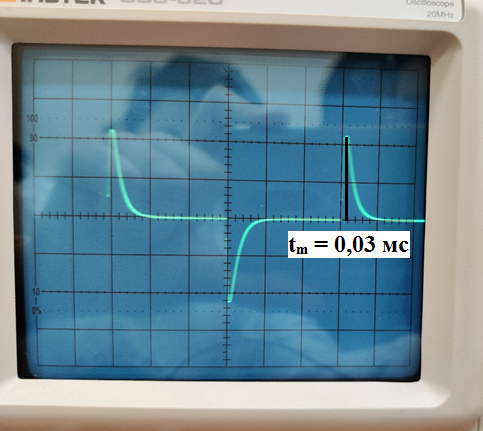
Рис. 14 - Определение собственой частоты при исследовании свободных процессов в цепи второго порядка (R­₁ = R_КР = 1,6 [кОм]).

p₁ = p₂ = - α = 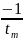= = 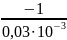-3,3∙10⁴

Таким образом, теоретически рассчитанные собственные частоты цепи приблизительно равны собственным частотам цепи, найденным по осциллограмме.

Определим свободный процесс:

U_R(t) = A₁e^-32000t + A₂te^-32000t

Отобразим диаграмму расположения собственных частот на комплексной плоскости:

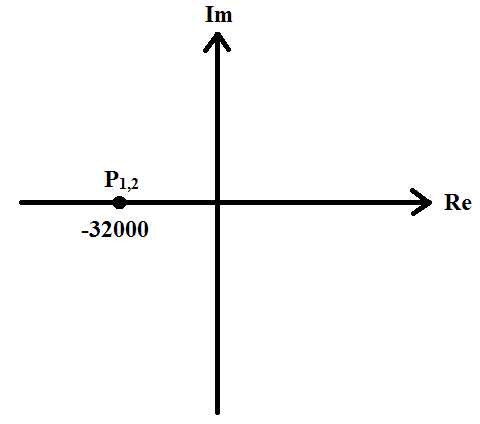
Рис. 15 - Диаграмма расположения собственных частот при исследовании свободных процессов в цепи второго порядка на комплексной плоскости

(R­₁ = R_КР = 1,6 [кОм]).

2.3. Снятие осциллограммы процесса при R₁ = 0 (незатухающий режим):

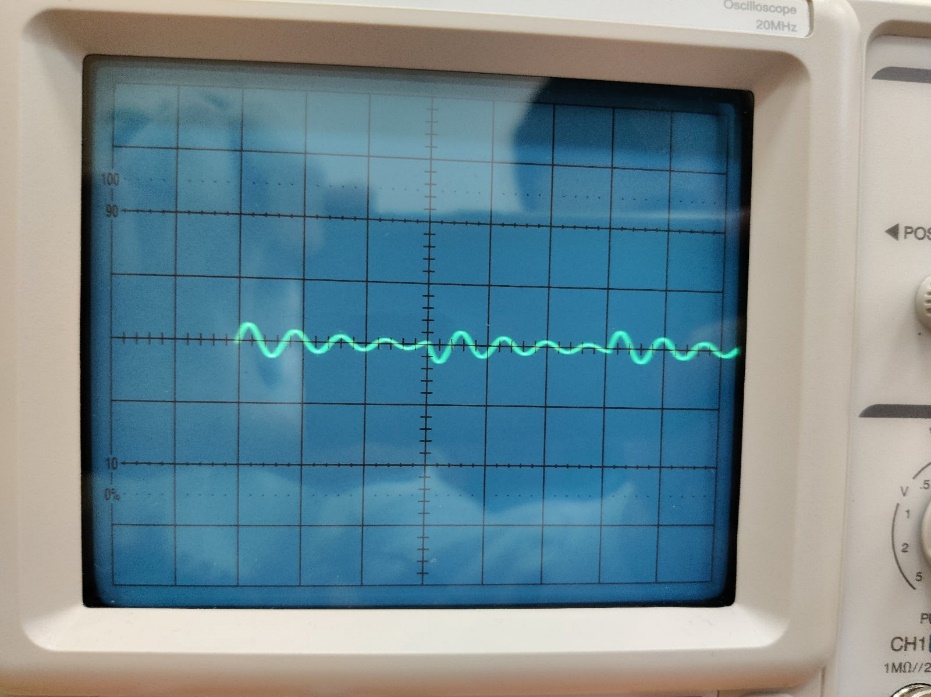
Рис. 16 – Осциллограмма при исследование свободных процессов в цепи второго порядка (R­₁ = 0).

Вычислим собственные частоты цепи теоретически:

p_1,2 = ± jω = ± j = ± 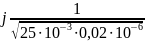= ± j44721

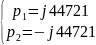
Вычислим собственные частоты цепи по осциллограмме:

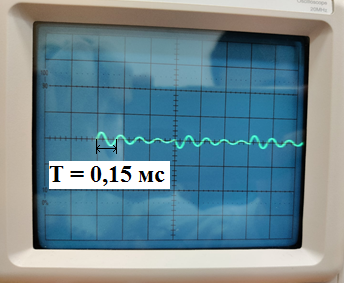
Рис. 17 - Определение собственой частоты при исследовании свободных процессов в цепи второго порядка (R­₁ = 0).

p_1,2 = ± jω = ± j = 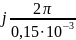= ±j41888

Таким образом, теоретически рассчитанные собственные частоты цепи приблизительно равны собственным частотам цепи, найденным по осциллограмме.

Определим свободный процесс:

U_R(t) = A₁cos(44721t)

Отобразим диаграмму расположения собственных частот на комплексной плоскости:

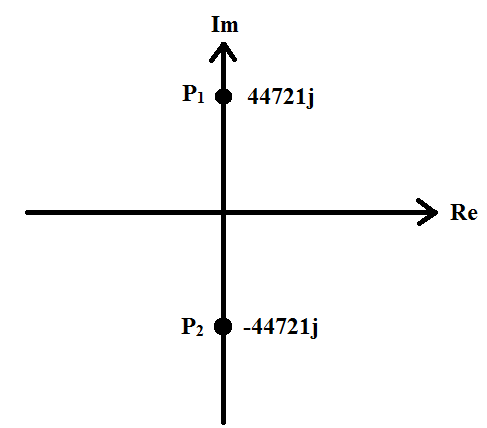
Рис. 18 - Диаграмма расположения собственных частот при исследовании свободных процессов в цепи второго порядка на комплексной плоскости

(R­₁ = 0).

Вычислим добротность контура:

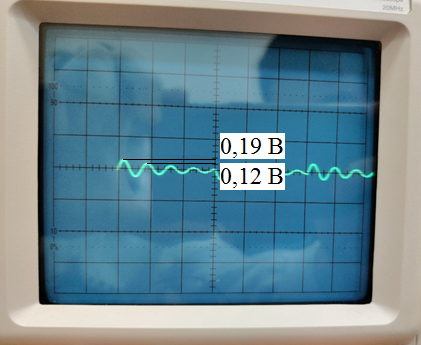
Рис. 19 - Определение добротности при исследовании свободных процессов в цепи второго порядка (R­₁ = 0).

Q = 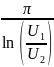= = 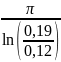6,84