Лабы Яшкардин / Лаба 2 / ТОЭ Лаба 2 0207 Маликов Отчет

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра теоретических основ электротехники

отчет

по лабораторной работе №2

по дисциплине «Теоретические основы электротехники»

Тема: Исследование линейных резистивных цепей

Студент гр. 0207		Маликов Б.И.
Преподаватель		Яшкардин Р.В.

Санкт-Петербург

2022

ЦЕЛЬ РАБОТЫ

Целью работы является экспериментальное исследование и анализ линейных разветвленных резистивных цепей с использованием методов анализа сложных цепей, а именно методов наложения, эквивалентного источника и принципа взаимности.

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

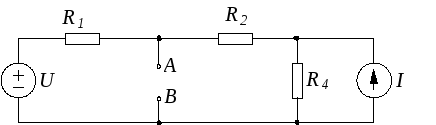
Рис. 1 – Резистивная цепь, заданная в данном эксперименте

В данной работе рассматривается линейная разветвленная резистивная цепь (рис. 1), включающая себя источники постоянного тока I и напряжения U. Также, данная цепь содержит резистивные элементы R₁, R₂, R₃ и R₄.

По указанию преподавателя, значение напряжения ИН устанавливают равным U = 4В или U = 2В, значение тока ИТ, так же по указанию преподавателя,

I  2 мА или I  1 мА. При этом, значение резистивных элементов следующие: R₁ = R₂ = 1,5 кОм, R₃ = R₄ = 3 кОм.

Определим основные методы анализа сложных цепей, необходимые для нахождения токов и напряжений в каждой из ветвей:

Рис. 2 – Метод наложения

1. Рассмотрим метод наложения. Метод наложения основан на том, что действие нескольких источников в цепи равен алгебраической сумме действий каждого из источников по отдельности. В нашем случае, в цепи действуют два источника, значит, необходимо рассмотреть два случая (рис. 2, а и б). В случае рисунка а, мы рассматриваем действие только источника напряжения, при этом ИТ -> ХХ. А в случае рисунка б, мы анализируем цепь с действующим ИТ, при этом ИН -> КЗ. Тогда, опираясь на Рис. 2, можно найти токи I₁, I₂, I₃ и I₄:

I₁ = I₁’ – I₁” (знак минус, так как противонаправленные), I₂ = I₂’ – I₂”,

I₃ = I₃’ + I₃” и I₄ = I₄’+I₄”.

Рис. 3 – Метод эквивалентного источника источника напряжения

2. Рассмотрим метод эквивалентного источника источника напряжения. Метод эквивалентного источника источника напряжения состоит в том, что, выбрав одну из ветвей цепи, цепь с несколькими источниками можно представить в виде цепи, состоящей из эквивалентного источника напряжения, в данном случае U₀ и сопротивлением R₀, соединенный последовательно (рис. 3а). Рис. 3а – эквивалентная схема для ветви 3. При этом, обозначим U₀ – напряжение холостого хода (напряжение при обрыве цепи на выводах А и Б) в ветви 3. R₀ – эквивалентное сопротивление цепи в случае исключения всех источников (ИН -> КЗ, ИТ -> ХХ) (рис. 3б). Тогда, ток I₃ находим следующим образом:

I₃ =

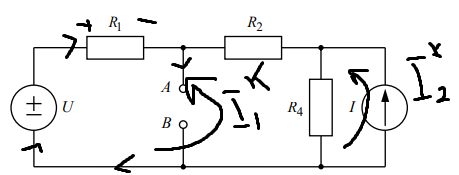
Рис. 4 – Принцип взаимности

Рассмотрим принцип взаимности. Принцип взаимности состоит в том, что если единственный в цепи ИН U (ИТ исключаем, ИТ -> ХХ), действующий в ветви 1, вызывает в ветви 3 ток I (рис. 4а), то, если перенести ИН в ветвь 3, то этот источник вызовет в ветви 1 такой же ток I (рис. 4б).

ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

2.2.1 Исследование цепи при питании её от двух источников

Проверим полученные результаты, занесённые в таблицу 2.1 протокола наблюдения, используя уравнения Кирхгофа:

Уравнения Кирхгофа для токов:

1. –I₁ – I₂ + I₃ = 0 = –0,23 – 0,34 + 0,57 = 0

2. –I + I₄ + I₂ = 0 = –1,03 + 0,69 +0,34 = 0

Уравнения Кирхгофа для напряжений:

1) –U₃ – U₁ + U = 0 = –1,64 – 0,36 + 2,00 = 0

2) –U₄ +U₂ +U₃ = 0 = -2,15 +0,5 + 1,64  0

Из расчетов видно, что экспериментально полученные измерения примерно совпадают с измерениями, полученными теоретически. Погрешность можно списать на инструментальную погрешность вольтметра.

2.2.2 Определение токов цепи методом наложения.

Для удобства перенесём таблицу 2.2 из протокола наблюдения

Таблица 2.2 протокола наблюдений

Включены источники	I1, мА	I2, мА	I3, мА	I4, мА
U	0,61	0,23	0,37	0,23
I	0,38	0,58	0,20	0,46
U, I	0,23	0,35	0,57	0,69

Определим по данным обоих опытов методом наложения токи в ветвях:

1. = 0,61 – 0,38 = 0,23 = 0,23

2. = 0,58 – 0,23 = 0,35  0,34

3. = 0,37 + 0,20 = 0,57 = 0,57

4. = 0,23 + 0,46 = 0,69 = 0,69

Произведя расчеты и сравнив полученные результаты с результатами из п. 2.2.1, видно, что результаты, полученные методом наложения, практически совпадают со значениями токов из п. 2.2.1.

2.2.3. Определение тока в ветви с сопротивлением R₃ методом эквивалентного источника напряжения.

Проверим данные, полученные экспериментальным путем, путем расчета цепи методом эквивалентного источника, используя параметры цепи:

В цепи: U = 2 В, I  1 мА, R₁ = R₂ = 1,5 кОм, R₃ = R₄ = 3 кОм.

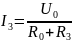
U₀ = U_AB = U – U₁ = 2 – I₁R₁

Воспользуемся методом контурных токов для нахождения тока I₁:

I₂^k = 1

6∙I₁^k – 3 = -2

I₁^k = 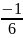= - 0,17 мА = I₁

R₀ = = = 1,125 кОм

U₀ = U_AB = U – U₁ = 2 – I₁R₁ = 2 + 0,17∙1.5 = 2,26 В

= = 0.54 мА

Результаты эксперимента: U₀ = 2.29 В, I₃ = 0.57 мА

По результатам расчетов можно сказать, что значения U₀ (2,26  2,29) и I₃ (0,54  0,57) примерно равны

2.2.4. Экспериментальная проверка принципа взаимности.

По результатам эксперимента:

I₃ = 0,37 мА

I₁ = 0,42 мА

Значения примерно равны, это говорит о наличии погрешности в измерениях.

ВЫВОД

1. При исследовании цепи от двух источников были найдены значения токов и напряжений на ветвях. Проверка показала, что ЗНК и ЗТК выполняются (2.2.1.)

2. Были определены токи цепи и найдены методом наложения токи в ветвях. Результаты показали, что найденные токи совпадают с токами, найденными в (2.2.1.)

I	2.2.1	2.2.2
I1, мА	0.23	0.23
I2, мА	0.34	0.35
I3, мА	0.57	0.57
I4, мА	0.69	0.69

3. Методом эквивалентного источника напряжения был измерен ток I­₃ (2.2.3.). Используя данные цепи, полученное значение было подтверждено результатами расчета цепи методом эквивалентного источника.

Результаты эксперимента: U₀ = 2.29 В, I₃ = 0.57 мА.

Результаты расчета: U₀ = 2.26 В, I₃ = 0.54 мА.

4. Эксперимент, проведенный в (2.2.4), показал, что принцип взаимности выполняется и:

I₃ = 0.37 мА

I₁ = 0.42 мА

Значения примерно равны.

ОТВЕТЫ НА КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Каковы результаты контроля данных в 2.2.1?

Ответ:

Контроль данных в пункте 2.2.1 был проведен с помощью уравнений Кирхгофа. При этом, как можно увидеть, конечные результаты измерений верны, а именно: данные, измеренные в ходе эксперимента, были проверены при помощи уравнений Кирхгофа и полностью подтвердились.

2. Изменятся ли токи ветвей, если одновременно изменить полярность напряжения ИН и направление тока ИТ на противоположные?

Ответ:

В случае изменения полярности напряжения ИН и направление тока ИТ, значения токов ветвей не изменятся, а изменятся только их изначальные направления течения (на противоположные). То есть, данное утверждение можно описать так:

3. Чему равно напряжение между узлами «C» и «D» цепи?

Ответ:

Напряжение между узлами «C» и «D» будет следующим: U_CD = U₁-U₂

Напряжение на R₁ будет равняться: U₁ = I₁R₁ = 0,23∙10^-3∙1500 = 0,345 В

Напряжение на R₂ будет равнятся: U₂ = I₂R₂ = 0,34∙10^-3∙1500 = 0,510 В

Тогда, U_CD = U₁-U₂ = 0,345 – 0,510 = - 0,165 в

4. Как изменить напряжение ИН, чтобы ток I₁ стал равен нулю?

Ответ:

В данной задаче легче всего использовать метод контурных токов, тогда, запишем систему (причем, I₄∙R₄ примем за U₄):

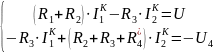
В нашем случае, I₁ = 0 =>

Выразим I₂^K:

I₂^K = -

Тогда:

∙(R₂+R₃+R₄) = U₁ => U = U₄∙ ,

где U₄ = I∙R₄ = 1,03∙10^-3∙3∙10³ = 3,09 В

U = 3,09∙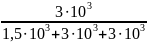 = 1,236 В

5. Почему рис. 2.4, б при U  U₀ реализует схему метода эквивалентного источника напряжения (рис. 2.3, а)?

Ответ:

Потому, что при U = U₀ в рис. 2.4, б мы получаем такое же эквивалентное сопротивление, как и в случае (рис. 2.3, а), тогда, исходя из формулы:

R₀ = , где I_K – ток КЗ ветви 3 (в обоих случаях одинаковый), можем сказать, что

R₀ = =

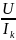
6. Чему будет равен ток 1 I , если ИН поместить в ветвь 4, а ИТ отключить?

Ответ:

Значение напряжения ИН, заданное преподавателем U = 2 В. Так как ИН помещается в ветвь 4, а ИТ отключается, то получаем следующее:

R₁₃ = = = 1 кОм

По ФДН:

U₁₃ = U₁ = U₃ = U∙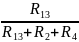 = 2∙ = 0,36 В

Тогда, ток I₁:

I₁ = = = 0,24 мА

7. Как проконтролировать результаты экспериментов в 2.2.2, 2.2.3 и 2.2.4?

Ответ:

Контроль результатов экспериментов происходит путем сравнения их с теоретическими расчетами. В п. 2.2.2 токи в цепи определялись методом наложения, при этом, результаты вычислений сопоставлялись с экспериментальными значениями пункта 2.2.1. В п. 2.2.3 ток в ветви с сопротивлением R₃ определялся методом эквивалентного источника напряжения, при этом, полученное значение сопоставлялось со значением тока, полученным экспериментально в 2.2.1. В п. 2.2.4 экспериментально рассматривался принцип взаимности, при этом, результаты двух экспериментов сравнивались между собой, а также, данные результаты сравнивались с расчетными значениями.