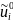Трегуб Типовики / Типовик 2 Мет. Мат. Физ
..docxМинистерство науки и высшего образования Российской Федерации
СПбГЭТУ «ЛЭТИ»
Кафедра высшей математики
Методы математической физики
Типовой расчет по теме:
«Решение уравнения теплопроводности методом Фурье и сеточным методом»
Вариант №11
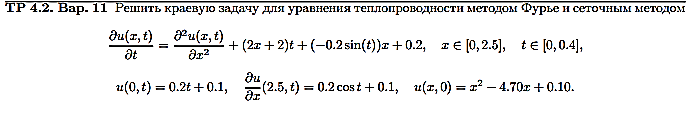
Выполнил: студент гр. №0207 Маликов Б. И.
Преподаватель: Трегуб В. Л.
Оценка: баллов
Санкт-Петербург
2022
I. Решение уравнения теплопроводности методом Фурье.
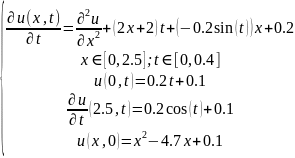
1. Сведем исходную задачу к задаче с однородными краевыми условиями. Для этого выполним замену u(x,t) = v(x,t) + w(x,t). Зададим w(x,t) = α(t)x + β(t) и подберем α(t) и β(t) так, чтобы функция w(x,t) удовлетворяла тем же краевым условиям, что и функция u(x,t):
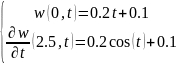
Тогда v(x,t) будет удовлетворять однородным условиям:
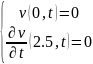
Подставляя w(x,t) в краевые условия, получим:
0.2t + 0.1 = v(0,t) + β(t) => β(t) = 0.2t + 0.1
0.2cos(t) +
0.1 =
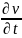 (2.5,t)
+ α(t) => α(t) = 0.2cos(t) + 0.1
(2.5,t)
+ α(t) => α(t) = 0.2cos(t) + 0.1
Значит:
w(x,t) = (0.2cos(t) + 0.1)x + 0.2t + 0.1
Найдем v(x,0):
u(x,t) = v(x,t) + (0.2cos(t) + 0.1) + 0.2t + 0.1
u(x,0) = x2 – 4.7x + 0.1 = v(x,0) + 0.3x + 0.1 => v(x,0) = x2 – 5x
Запишем краевую задачу относительно функции v(x,t):
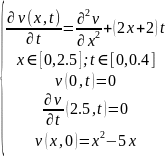
Данную задачу
решим методом Фурье. Функцию v(x,t)
будем искать в виде ряда по собственным
функциям оператора Lx(v)
= -
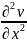 .
.
2. Решим задачу Штурма-Лиувилля.
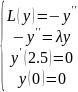
λ= μ2 > 0 => y(x) =C1cos(μx) + C2sin(μx)
Тогда:
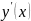 =
-μC1sin(μx)
+μC2cos(μx)
=
-μC1sin(μx)
+μC2cos(μx)
При x = 0:
 = C1cos(0)
+ C2sin(0)
= 0 => C1
= 0
= C1cos(0)
+ C2sin(0)
= 0 => C1
= 0
При x = 2.5:
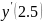 = μC2cos(2.5μ)
= 0
= μC2cos(2.5μ)
= 0
Тогда:
y(x)
= C2sin(μx),
C2
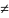 0.
0.
Найдем собственные числа и собственные функции оператора Штурма-Лиувилля рассматриваемой задачи:
cos(2.5μ)
= 0 => 2.5μk
=
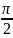 + πk;
=> μk
=
+ πk;
=> μk
=
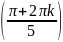 ,
k
= 0, 1, 2, …
,
k
= 0, 1, 2, …
Тогда, собственные числа:
λk
= μk2
=
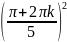 ,
k
= 0, 1, 2, …
,
k
= 0, 1, 2, …
И собственные функции:
yk(x)
= sin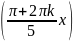 ,
k
= 0, 1, 2, …
,
k
= 0, 1, 2, …
3. Функцию v(x,t)
найдем в виде ряда Фурье по найденным
собственным функциям дифференциального
оператора yk(x):
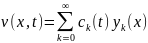
Функции f(x,t) = (2x+2)t и φ(x) = x2 – 5x также разложим в ряды Фурье:
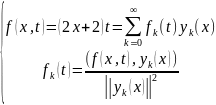
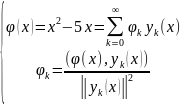
Вычислим
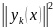 и скалярные произведения:
и скалярные произведения:
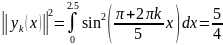
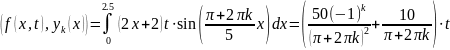

Вычислим коэффициенты Фурье:
fk(t)
=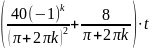
φk
=
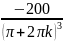
Выполним подстановку в уравнение:
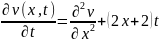
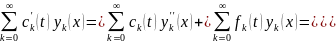
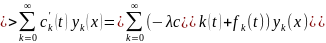
Подставим ряды в начальное условие v(x,0) = x2 – 5x:
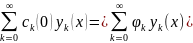
Тогда:
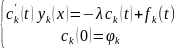
Воспользуемся методом неопределенных коэффициентов. Найдем общее решение однородного уравнения:
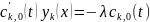
Тогда:
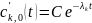
Частное решение неоднородного уравнения найдем в виде:
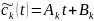
Тогда:
Ak = -λk(Akt + Bk) + Gkt
где:
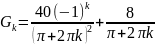
Найдем Ak и Bk:
Ak
= (-λkAk
+ Gk)t
– λkBk
=>
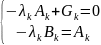 =>
=>
=>
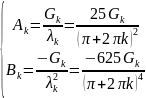
Запишем общее решение неоднородного уравнения:
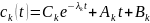
где:
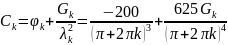
Окончательное решение задачи Коши имеет вид:
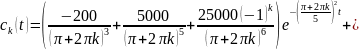
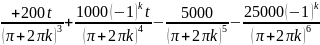
При найденных значениях ck(t), искомая функция v(x,t) представляется в виде ряда:
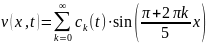
4. Получим решение исходной задачи u(x,t):
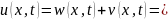
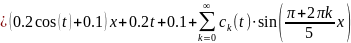
5. Найдем приближенное решение исходной задачи, используя N-ю частичную сумму ряда Фурье при N = 6, в точках x1, … ,x6, разбив промежуток [0, l] на 5 частей при t = T =0.4:
xi
=
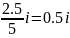
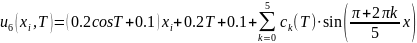
Значения первых 6 коэффициентов ck(T) ряда Фурье:
k |
0 |
1 |
2 |
3 |
4 |
5 |
ck(T) |
− 5.0068 |
− 0.0368 |
0.0195 |
0.0051 |
0.0038 |
0.0016 |
Значения функции u(x,T) в точках x1, … , x6:
x |
0 |
0.5 |
1 |
1.5 |
2 |
2.5 |
u(x,T) |
0.180 |
− 1.231 |
− 2.520 |
− 3.472 |
− 3.991 |
− 4.063 |
II. Решение уравнения теплопроводности по явной разностной схеме.
Обозначим:
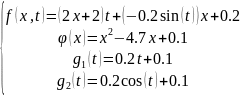
Разобьем точками x0, … , xn промежуток [0, l] на n равных частей и точками
t0,…, tm промежуток [0, T] на равных частей (n = m = 5). Получим сетку, покрывающую область Ω = [0, l] x [0, T]. Обозначим (xi, tj) узлы сетки.
Вычислим шаги сетки по осям Ox и Ot:
h
=
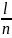 =
=
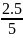 = 0.5
= 0.5
τ
= =
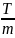 =
=
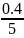 = 0.08
= 0.08
Обозначим
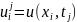 – значение искомой функции в узле (xi,
tj).
– значение искомой функции в узле (xi,
tj).
Для нулевого временного слоя (xi, t0), i = 0, … , n, используем начальное условие:
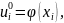 i
= 0, … , n
i
= 0, … , n
В узлах сетки (xi, tj) i = 1, …, n; j = 0, …, m – 1 запишем дифференциальное уравнение, заменив производные соответствующим разностным отношением:
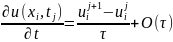
и:
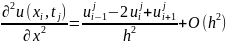
Запишем:
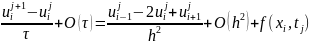
i = 1, …, n – 1; j = 0, …, m − 1;
В граничных узлах сетки (x0, tj+1) и (xn, tj+1), j = 0, …, m – 1 запишем заданные краевые условия:
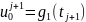
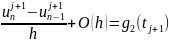
Получим явную
разностную схему для уравнения
теплопроводности – систему уравнений
относительно неизвестных
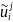 (приближенных
значений u(x,t)
в узлах сетки):
(приближенных
значений u(x,t)
в узлах сетки):
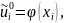 i = 0, …
, n
i = 0, …
, n
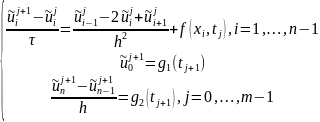
Вычислим значение функции на нулевом временном слое:
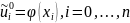
Определим значения
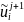 на следующих временных слоях во внутренних
точках:
на следующих временных слоях во внутренних
точках:
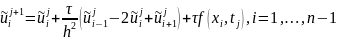
и граничных точках:
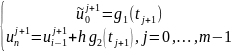
Проверим выполнение условия устойчивости явной разностной схемы. Условия устойчивости:
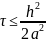
В данной задаче:
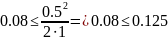
Условие выполнено, применение явной разностной схемы возможно.
Вычислим значение функции на нулевом временном слое при t = 0:
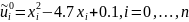
i |
0 |
1 |
2 |
3 |
4 |
5 |
x |
0 |
0.5 |
1 |
1.5 |
2 |
2.5 |
|
0.100 |
− 2.000 |
− 3.600 |
− 4.700 |
− 5.300 |
− 5.400 |
Для краевого условия при x = 0 найдем значение функции:
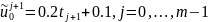
i |
0 |
1 |
2 |
3 |
4 |
|
0.08 |
0.16 |
0.24 |
0.32 |
0.40 |
|
0.116 |
0.132 |
0.148 |
0.164 |
0.180 |
Вычислим значения :
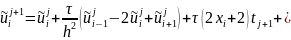
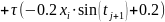
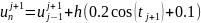
i = 1, … , n – 1; j = 0, …, m – 1; x = xn = 2.5;
Получим решение задачи по явной разностной схеме:
j \ i |
0 |
1 |
2 |
3 |
4 |
5 |
0 |
0.100 |
− 2.000 |
− 3.600 |
− 4.700 |
− 5.300 |
− 5.400 |
1 |
0.116 |
− 1.824 |
− 3.424 |
− 4.524 |
− 5.124 |
− 4.974 |
2 |
0.132 |
− 1.681 |
− 3.224 |
− 4.318 |
− 4.832 |
− 4.684 |
3 |
0.148 |
− 1.541 |
− 3.015 |
− 4.056 |
− 4.532 |
− 4.385 |
4 |
0.164 |
− 1.401 |
− 2.788 |
− 3.769 |
− 4.209 |
− 4.064 |
5 |
0.180 |
−1.254 |
− 2.545 |
− 3.460 |
− 3.863 |
− 3.720 |
III. Решение уравнения теплопроводности по неявной разностной схеме.
Заданную краевую задачу запишем в узлах сетки, покрывающей область Ω.
Для нулевого временого слоя (xi,t0), i = 0, …, n, используя начальное условие:
i = 0, … , n
В узлах сетки (xi,tj), i = 1, …, n – 1; j = 1, …, m, запишем дифференциальное
уравнение, заменив производные разностным отношением, но производную по
времени аппроксимируем, используя разностное отношение «назад»:
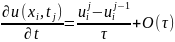
Вторую производную по x аппроксимируем симметричным разностным
отношением:
Получим:

i = 1, …, n – 1; j = 0, …, m;
В граничных узлах сетки (x0, tj) и (xn, tj), j = 0, …, m , запишем заданные краевые условия:
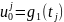
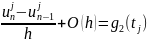
Неявная схема разностной аппроксимации заданной краевой задачи:
i = 0, … , n
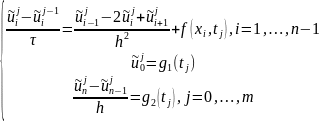
где - приближенное значение функции u(x,t) в узлах сетки.
Для выполнения расчетов перепишем уравнение в виде:
i = 0, … , n
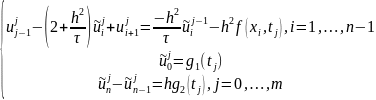
Из начального
условия
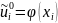 (i
= 0, … , n)
определяются значения
для нулевого временного слоя.
(i
= 0, … , n)
определяются значения
для нулевого временного слоя.
Значения (i = 0, … , n) для следующих временных слоев tj (j = 1, …, m) можно найти, решая систему линейных уравнений.
Кратко эту систему можно записать:
A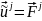
Найдем
преобразованную матрицу
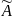 :
:
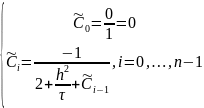
Запишем матрицу :
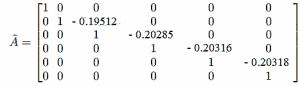
Определим правые части систем для всех временных слоев:
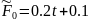
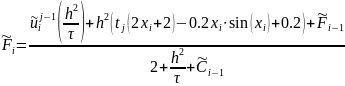
i =1, …, n-1
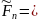
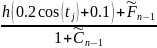
Для решения систем уравнений с матрицей коэффициентов будем использовать
следующие формулы (обратный ход метода прогонки):
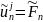
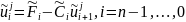
Последовательно решим системы уравнений с верхней треугольной матрицей
Коэффициентов для временных слоев 1, …, 5:
1-й t слой: 2-й t слой:

3-й t слой: 4-й t слой:
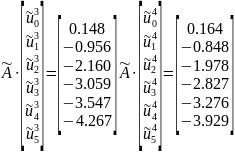
5-й t слой:
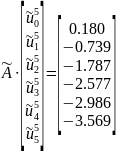
Решение задачи по неявной разностной схеме:
j \ i |
0 |
1 |
2 |
3 |
4 |
5 |
0 |
0.100 |
− 2.000 |
− 3.600 |
− 4.700 |
− 5.300 |
− 5.400 |
1 |
0.116 |
− 1.840 |
− 3.404 |
− 4.483 |
− 5.026 |
− 4.877 |
2 |
0.132 |
− 1.687 |
− 3.191 |
− 4.233 |
− 4.731 |
− 4.583 |
3 |
0.148 |
− 1.534 |
− 2.963 |
− 3.956 |
− 4.414 |
− 4.267 |
4 |
0.164 |
− 1.379 |
− 2.720 |
− 3.654 |
− 4.074 |
− 3.929 |
5 |
0.180 |
− 1.220 |
− 2.462 |
− 3.331 |
− 3.711 |
− 3.569 |