КЭТ Лабы Грязнов / 5 Лаба / КЭТ Лаба 5 Отчет

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра электронных приборов и устройств

отчет

по лабораторной работе №5

по дисциплине «Компоненты электронной техники»

Тема: Исследование параметров катушки индуктивности

Студенты гр. 0207 _________________ Маликов Б.И.

_________________ Бурчик Н.Е.

Преподаватель _________________ Грязнов А.Ю.

Санкт-Петербург

2022

ЦЕЛЬ РАБОТЫ

Ознакомление с основными параметрами катушек индуктивности и методами их измерений.

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

Движущиеся заряды порождают магнитное поле. Магнитное поле имеет направленный характер и характеризуется векторной величиной В, называемой электромагнитной индукцией.

Напряженность магнитного поля - вспомогательная величина Н, аналогичная вектору электрического смещения D.

Связь между В и Н определяется формулой:

(1.1)

где ₀ = 410^-7 Гн/м - магнитная проницаемость вакуума (воздуха); μ – относительная магнитная проницаемость вещества по отношению к вакууму.

Магнитное поле удается сконцентрировать внутри катушки, образованной множеством близко расположенных витков с током I. Если принять, что все составляющие индукции по сечению катушки S равны некоторому среднему значению В, что справедливо для катушек с сердечником, то отдельные значения B суммируются в полный поток электромагнитной индукции, или магнитный поток, определяемый как

 = B∙S = L∙I (1.2)

Индуктивность зависит от геометрии катушки, от магнитной проницаемости сердечника и магнитных свойств окружающей среды. Так, для дросселей с замкнутыми тороидальными магнитопроводами индуктивность определяется формулой

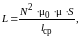(1.3)

Единицей индуктивности является генри [Гн]. Одному генри соответствует индуктивность катушки без сердечника, которая развивает поток электромагнитной индукции в 1 Вб (вебер) в результате протекания тока 1 А.

В соответствии с законом Ленца изменение магнитного потока Ф, пронизывающего замкнутый контур, порождает в нем индуцированную ЭДС (Е):

(1.4)

Выражение для ЭДС катушки индуктивности при изменении протекающего через нее тока:

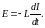(1.5)

Включение индуктивности последовательно с цепью нагрузки, питаемой пульсирующим источником тока, снижает его пульсации за счет возникающей ЭДС самоиндукции.

Если предположить, что ток в катушке изменяется от некоторого значения I до нуля, то работа, совершаемая этим током за время dt, будет определяться как

dA = EIdt (1.6)

Если индуктивность не зависит от тока, очевидно, что магнитное поле является носителем энергии, за счет которой и совершается данная работа. Таким образом, катушка L, через которую протекает ток I, запасает энергию W, равную

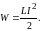(1.7)

Катушка не может запасти энергию мгновенно. Ее нужно зарядить аналогично тому, как заряжают конденсатор. Если индуктивность подключается к источнику постоянного напряжения U, то ее зарядка происходит по экспоненциальному закону:

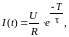(1.8)

где R – полное активное сопротивление, ограничивающее ток индуктивности; τ = L/R – постоянная времени зарядки индуктивности.

Цепь, состоящую из катушки индуктивности и параллельно подключенного ей конденсатора, называют колебательным контуром. При работе индуктивности в составе колебательного контура ее периодическая зарядка и разрядка происходят на резонансной частоте контура:

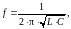(1.9)

где С – емкость конденсатора, входящего в колебательный контур.

Поскольку в колебательном контуре происходит периодическое превращение энергии, запасенной в катушке индуктивности, в энергию заряженного конденсатора, то в отсутствие потерь справедливо:

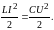(1.10)

Поскольку работа контура сопровождается потерями энергии, используют понятие добротности колебательного контура, характеризующее скорость затухания колебаний.

(1.11)

где Ne – число колебаний, в течение которых амплитуда снижается в е раз.

Рисунок 1. Схема колебательного контура.

ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

1. Расчет теоретического и практического значений индуктивности исследуемой катушки для N = 20.

В лабораторной работе используется сердечник с μ = 2500, l_ср = 78 [мм], S = 54 [мм²].

Теоретическое значение индуктивности по формуле (1.3):

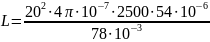= 0.87 [мГн]

Практическое значение индуктивности:

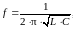=> = 0.72 [мГн]

2. Расчет добротности колебательного контура.

Вычисление добротности по формуле (1.11):

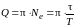
Где вычисляется по формуле:

=>

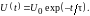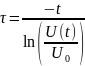
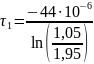= 71.1 [мкс]

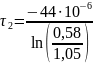= 74.1 [мкс]

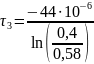= 118.4 [мкс]

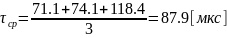
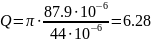
3. Исследование зависимости индуктивности катушки от количества витков.

Вычисление теоретических и экспериментальных значений индуктивности при различных витках катушки:

Пример расчета для 18 витков:

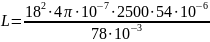= 0.70 [мГн]

= 0.60 [мГн]

Таблица 1.

Теоретическое и практическое значений величины индуктивности исследуемой катушки.

Кол-во витков	8	10	12	14	16	18	20
Lтеор, мГн	0.14	0.22	0.31	0.43	0.56	0.70	0.87
Lпракт, мГн	0.15	0.22	0.29	0.38	0.48	0.60	0.72

Рисунок 2. Зависимость индуктивности от количества витков катушки.

4. Исследование зависимости частоты колебательного контура от индуктивности.

Вычисление теоретических значений частоты колебательного контура по формуле (1.9):

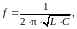
Катушка EC24-240R:

f =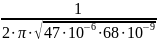 = 89025 [Гц]

Катушка B82141A:

f =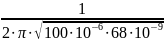 = 61033 [Гц]

EC24-240R параллельно B82141A:

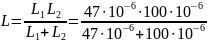= 31.97 [мкГн]

f =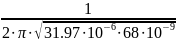 = 107942 [Гц]

EC24-240R последовательно с B82141A:

L = L₁ + L₂ = 147 мкГн

f =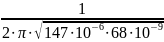 = 50339 [Гц]

Вычисление экспериментального значения частоты по формуле:

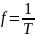
Катушка EC24-240R:

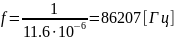
Катушка B82141A:

EC24-240R параллельно B82141A:

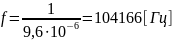
EC24-240R последовательно с B82141A:

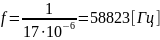
Рисунок 3. Зависимость частоты колебательного контура от индуктивности.

ВЫВОД

В ходе данной лабораторной работы была получена зависимость индуктивности катушки от количества витков. Анализируя теоретические и экспериментальные данные можно прийти к выводу, что:

1. Значения лежат примерно в одном диапазоне, что говорит о правдивости эксперимента.

2. При уменьшении числа витков катушки индуктивность также уменьшается.

Также была вычислена добротность Q = 6.28. Добротность обычно бывает в пределах 15 – 350, что говорит о низком качестве работы исследуемой катушки в цепях переменного тока.

Была исследована зависимость частоты колебательного контура от индуктивности катушек EC24-240R и B82141A при отдельном подключении, последовательном и параллельном. В итоге получили график зависимости, по которому можно сделать вывод, что с увеличением индуктивности уменьшается частота.