Лабы 2 Семестр / 0207 Маликов Отчет Лабораторная работа №8
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра физики
ОТЧЕТ
по лабораторной работе №8
ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЙ ТОКОПРОВОДЯЩИХ МОДЕЛЕЙ ПРИ ПОМОЩИ МОСТА УИТСТОНА
Выполнил: Маликов Б.И.
Группа № 0207
Преподаватель: Шишкина М.Н.
Вопросы |
Задачи ИДЗ |
Даты коллоквиума |
Итог |
|||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
||||||||||
|
||||||||||
|
||||||||||
|
||||||||||
Санкт-Петербург
2021
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
1. Выведем формулу для px1 :
Эскиз модели коаксиального кабеля:
Для коаксиального кабеля:
По
формуле:
;
=>
=>
=>
;
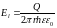Значит:
;
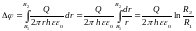Так
как
=>
;
RC=εε0
=>
2. Выведем формулу для px2 :
Эскиз модели двухпроводной линии:
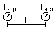
Для двухпроводной линии:
По
формуле:
;
=> => => ;
;
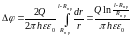Так
как
,
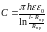значит
;
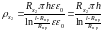3. Рассчитаем Rx1 и Rx2:
По
формуле: Rx
=
∙R3
1:
(Rx1)1 = 1∙980 = 980 [Ом]
(Rx1)2 = 0,5∙1920 = 960 [Ом]
(Rx1)3=2∙533 = 1066 [Ом]
Упорядочим выборку в порядке возрастания:
Rx1={960; 980; 1066} [Ом]
Промахи отсутствуют.
Рассчитаем среднее выборочное значение:
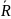x1=
=
= 1002 [Ом]
Рассчитаем СКО среднего:
SRx1 = 32,52 [Ом]
Определим случайную погрешность:
△Rx1=tp,N∙SRx1=4,3∙32,52=139,84 [Ом]
Рассчитаем полную погрешность:
△ x1=139,84 [Ом]
Запишем результат измерения:
Rx1=(1,0
0,1)∙103
[Ом]
2:
(Rx2)1 = 1∙1731,5 = 1732 [Ом]
(Rx2)2 = 0,5∙3470,5 = 1735 [Ом]
(Rx2)3=2∙881 = 1762 [Ом]
Упорядочим выборку в порядке возрастания:
Rx2={1732; 1735; 1762} [Ом]
Промахи отсутствуют.
Рассчитаем среднее выборочное значение:
x2=
=
= 1743 [Ом]
Рассчитаем СКО среднего:
SRx2 = 9,54 [Ом]
Определим случайную погрешность:
△Rx2=tp,N∙SRx1=4,3∙9,54=41,02 [Ом]
Рассчитаем полную погрешность:
△ x2=41,02 [Ом]
Запишем результат измерения:
Rx2=(1,74 0,04)∙103 [Ом]
4. Рассчитаем px1 и px2:
=>
1:
(px1)2
=
=
0,38 [Ом∙м]
(px1)2
=
=
0,37 [Ом∙м]
(px1)3=
=
0,42 [Ом∙м]
Упорядочим выборку в порядке возрастания:
px1={0,37; 0.38; 0,42} [Ом∙м]
Промахи отсутствуют.
Рассчитаем среднее выборочное значение:
x1=
0,39
[Ом∙м]
Рассчитаем СКО среднего:
Spx1 = 0,015 [Ом∙м]
Определим случайную погрешность:
△ px1=tp,N∙Spx1=4,3∙0,015=0,06 [Ом∙м]
Рассчитаем полную погрешность:
△ x1=0,06 [Ом∙м]
Запишем результат измерения:
px1=(0,39 0,06) [Ом∙м]
2:
=>
(px2)2
=
=
0,25 [Ом∙м]
(px2)2
=
=
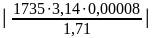0,25 [Ом∙м]
(px2)3=
=
0,26 [Ом∙м]
Упорядочим выборку в порядке возрастания:
px2={0,25; 0,25; 0,26} [Ом∙м]
Промахи отсутствуют.
Рассчитаем среднее выборочное значение:
x1= 0,253 [Ом∙м]
Рассчитаем СКО среднего:
Spx1 = 0,003 [Ом∙м]
Определим случайную погрешность:
△ px1=tp,N∙Spx1=4,3∙0,003=0,013 [Ом∙м]
Рассчитаем полную погрешность:
△ x1=0,013 [Ом∙м]
Запишем результат измерения:
px1=(0,253 0,013) [Ом∙м]
ВЫВОД
В ходе данной лабораторной работы были получены данные, на основании которых смогли вычислить значения сопротивлений Rx1 и Rx2 и удельных сопротивлений материалов токопроводящих моделей x1 и x2 для двух моделей. В конечном итоге, сравнивая значения, можно сделать вывод о том, что в двух случаях использовали разные материалы проводников.