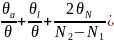Лабы 3 Семестр / 0207 Маликов Отчет Лабораторная работа №2
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра физики
ОТЧЕТ
по лабораторной работе №2
ОПРЕДЕЛЕНИЕ ДЛИНЫ СВЕТОВОЙ ВОЛНЫ С ИСПОЛЬЗОВАНИЕМ БИПРИЗМЫ
Выполнил: Маликов Б.И.
Группа № 0207
Преподаватель: Мазуренко В.С.
Вопросы |
Задачи ИДЗ |
Даты коллоквиума |
Итог |
|||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
||||||||||
|
||||||||||
|
||||||||||
|
||||||||||
Санкт-Петербург
2021
ЦЕЛЬ РАБОТЫ
Определение длины световой волны интерференционным методом.
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ
Экспериментальная установка состоит из оптической скамьи с мерной линейкой; бипризмы Френеля, закреплённой в держателе; источника света со светофильтром; раздвижной щели; окуляра со шкалой. Источником света служит лампа накаливания. Светофильтр, расположенный перед лампой, пропускает определенную часть спектра излучения лампы, которую и надлежит изучить. На оптической скамье, снабженной линейкой с миллиметровой шкалой, помещены укрепленные на держателях вертикальная щель S, бипризма Р и окуляр О. Ширину щели можно изменять с помощью винта, находящегося в верхней части его оправы. Щель и бипризма могут быть повернуты вокруг горизонтальной оси, а бипризма также и вокруг вертикальной оси.
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
Один из способов наблюдения интерференции световых волн основан на использовании бипризмы Френеля. Бипризма Френеля - две призмы с очень малым преломляющим углом , сложенные основаниями. От источника света S (щели) лучи падают на обе половины бипризмы Р, преломляются в ней и за призмой распространяются так, как если бы исходили из двух мнимых источников S1 и S2. За призмой имеется область пространства, в которой световые волны, преломлённые верхней и нижней половинами бипризмы, перекрываются.
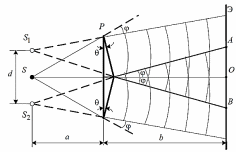
В этой области пространства сводятся воедино две части каждого цуга волн от источника S, прошедшие разные оптические пути, способные при выполнении условия lког 2/ интерферировать, где Δ – оптическая разность хода лучей, lког – длина когерентности, λ – средняя длина волны излучения, Δλ – интервал длин волн, представленных в данной волне. При этом колебания в точках, удалённых на расстояние большее lког вдоль распространения волны, оказываются некогерентными.
![]() Интерференционная
картина, получающаяся при этом,
соответствует интерференции волн,
исходящих из двух когерентных источников,
расположенных в точках S1 и S2, и на экране
Э в области АВ наблюдается тогда ряд
светлых и тёмных полос, параллельных
ребру бипризмы. Расстояние x
между светлыми (или тёмными) полосами
интерференционной картины составляет:
Интерференционная
картина, получающаяся при этом,
соответствует интерференции волн,
исходящих из двух когерентных источников,
расположенных в точках S1 и S2, и на экране
Э в области АВ наблюдается тогда ряд
светлых и тёмных полос, параллельных
ребру бипризмы. Расстояние x
между светлыми (или тёмными) полосами
интерференционной картины составляет:
где a и b ― расстояния от щели до бипризмы и от бипризмы до экрана; l = a + b; λ0 ― длина волны излучения источника в вакууме; d ― расстояние между мнимыми источниками, равное d = 2atg 2a.
Для расстояния d получаем:
d = 2a(n-1)
C учётом этого соотношения, имеем:
x = l0/2a(n-1) или 0 = 2a(n-1)x/l.
Данные выражения устанавливают связь между длиной световой волны и геометрическими размерами системы (т. е. источник света – бипризма Френеля – экран), в которой реализуется явление интерференции.
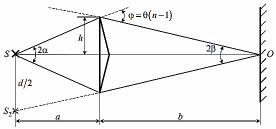
Видимость интерференционной картины зависит от размеров источника света. Существенным является угол 2. Угол 2 между соответствующими лучами, идущими от S через каждую из двух ветвей интерферометра к О, представляет собой угол раскрытия лучей, определяющий интерференционный эффект в точке О. Практически то же значение имеет этот угол и для любой другой точки интерференционного поля. Этот угол называется апертурой интерференции. Ему соответствует в поле интерференции угол схождения лучей 2, величина которого связана с углом 2 правилами построения изображений.
Из рисунка видно, что:
2 d/(a+b).
Получим выражение для расстояния между интерференционными полосами:
x = /(2).
Из рисунка видно также, что: + = = (n-1), и, кроме того, h/a , h/b . Исключая из двух последних выражений величину h, получаем =a/b.
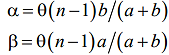 Для
углов
и
находим:
Для
углов
и
находим:
Условие хорошего наблюдения интерференции от протяжённого источника ширины s можно записать в виде: stga ≤ /4.
Для того, чтобы интерференционная картина при данных значениях и обладала высокой видимостью, приходится ограничиваться наблюдением интерференционных полос, порядок которых много меньше предельного mmax, определяемого условием:
mmax /
Экспериментально определяемая ширина полос рассчитывается по формуле:
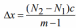
где m ― число полос, которые по яркости хорошо видны на экране, N1 и N2 – положения первой и последней полосы этого набора в делениях шкалы окуляра, c = 0,1 мм/ дел ― масштабный множитель.
Ширина области перекрытия волн на экране имеет протяженность AB = 2btgφ = 2bφ = 2b(n-1)θ. Тогда максимальное число интерференционных полос, которое можно наблюдать на экране с учетом формулы равно:
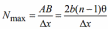 или
или
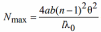
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
1.
Рассчитаем выборочным методом длину
волны излучения источника λ0
=
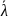
λ для N = 5 и P = 95%:
λ для N = 5 и P = 95%:
1.1 Упорядочим выборку в порядке возрастания:
λ0 = {417,29;494,83;535,20;560,58;565,19} [нм]
1.2 Рассчитаем среднее выборочное значение:
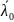 =
514,62 [нм]
=
514,62 [нм]
1.3 Рассчитаем СКО среднего:
S
λ0
-=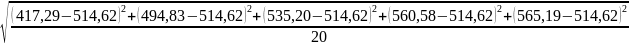 =27,34 [нм]
=27,34 [нм]
1.4 Определим случайную погрешность по коэффициенту Стьюдента при N=5 и P=95%: tp,N=2,8 – по таблице;
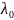 =
tp,N∙
SF
=>
=
76,55 [нм]
=
tp,N∙
SF
=>
=
76,55 [нм]
1.5 Рассчитаем полную погрешность результатов измерений, при Ѳ = 18,84 [нм]:
=
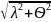 =>
=78,83
[нм]
=>
=78,83
[нм]
1.6 Запишем результат измерений в округлённой форме:
λ0 = 514,6 ± 78,8 [нм]
2. Вычислим по формулам для одного из опытов апертуру интерференции 2α и угол схождения лучей 2β:
По
формулам: α
=
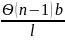 и β
=
,
учитывая, что l
= a
+ b,
для пятого значения получим:
и β
=
,
учитывая, что l
= a
+ b,
для пятого значения получим:
2α
=
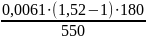 = 0,0020 [рад]
= 0,0020 [рад]
2β
=
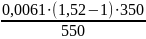 = 0,0042 [рад]
= 0,0042 [рад]
3. Оценим допустимые размеры источника (ширину щели s) для данной апертуры 2α:
По
формуле:
s∙tga
≤
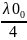 ,
получим: s
≤
,
получим: s
≤
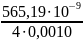 => s
≤
0,00014 [м]
=> s
≤
0,00014 [м]
4. Определим максимальный порядок интерференции mmax , при котором происходит обрыв ИК на экране, и по известному из опыта значению длины волны λ0 излучения источника рассчитаем интервал его немонохроматичности (полосу пропускания светофильтра), длину lког и время tког когерентности его излучения:
По
формуле:
mmax
=
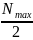 =
=
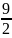 ≈ 5
≈ 5
mmax
=
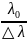 => △λ
=
=> △λ
=
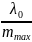 =
=
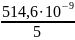 = 102,9 [нм]
= 102,9 [нм]
lког
≈
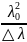 ≈
≈
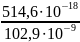 = 2573,5
[нм]
= 2573,5
[нм]
tког
=
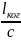 =
=
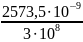 = 8,58 [фс]
= 8,58 [фс]
5. Сопоставим максимальное число полос Nmax , наблюдаемое в опыте, с рассчитанным по формуле по экспериментально определенной ширине линий, и по формуле для длины волны зеленого света λ0 = 550 нм:
По
формуле: Nmax
=
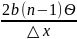 =
=
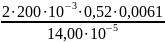 ≈ 9
≈ 9
Nmax
=
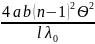 =
=
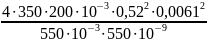 ≈ 9
≈ 9
Максимальное число полос Nmax , наблюдаемое в опыте: Nmax ≈ 9
ВЫВОД
В ходе данной работы были получены данные, на основании которых нам удалось вычислить значение длины волны зеленого света. Полученное значение, а именно: (514,6 ± 78,8) [нм], с учетом погрешности, входит в рамки спектра зеленого света. Также, сравнив значения Nmax наблюдаемое в опыте и рассчитанное по двум разным формулам (по формуле для длины волны и по формуле по экспериментально определенной ширине линий), можно сделать вывод о том, что Nmax было определено верно.
ПРОТОКОЛ НАБЛЮДЕНИЙ
ЛАБОРАТОРНАЯ РАБОТА №2
с |
θ |
n |
Nmax |
мм/дел |
Рад |
|
|
|
|
|
|
ОПРЕДЕЛЕНИЕ ДЛИНЫ СВЕТОВОЙ ВОЛНЫ С ИСПОЛЬЗОВАНИЕМ БИПРИЗМЫ
№ |
a |
N1 |
N2 |
m |
x
=
|
λ0
=
|
|
|
мм |
дел |
дел |
|
мм |
нм |
нм |
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
Выполнил: Маликов Б.И.
Преподаватель: Мазуренко В.С.

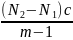
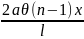
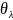 =
λ(
=
λ(