
ЛБ 2
.pdf
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральноегосударственноеавтономноеобразовательноеучреждениевысшегообразования
«НАЦИОНАЛЬНЫЙИССЛЕДОВАТЕЛЬСКИЙТОМСКИЙПОЛИТЕХНИЧЕСКИЙУНИВЕРСИТЕТ»
Школа базовой инженерной подготовки Отделение общетехнических дисциплин
ОТЧЕТ ПО ПРАКТИЧЕСКО-ЛАБОРАТОРНОЙ РАБОТЕ № 2
Определение механических параметров звеньев механизма (геометрия масс)
по дисциплине:
МЕХАНИКА
Исполнитель: |
|
|
|
студент группы |
5А07 |
Шкарпетин А.С |
19.04.2022 |
|
|
Сергеев А.С |
|
Руководитель: |
|
|
|
преподаватель |
|
Черемискина М.С. |
|
Томск – 2022
Определение механических параметров звеньев механизма (геометрия масс) Цель работы: Ознакомление с методикой экспериментального определения центра тяжести и момента инерции тела, имеющего ось вращения, не проходящую через центр тяжести.
Порядок выполнения работы по определению величины момента инерции звенаметодом физического маятника
1.Определить массу звена m.
2.Определить положение центра тяжести звена S.
3.Выбрать точку подвеса О и измерить расстояние от точки подвеса до центра тяжести lS (измерение проводить с точностью до 1 мм). Привести
эскиз.
4.Определить период колебаний Т.
5.Период колебания звена подсчитывается как среднее из трёх замеров
времени 20-30 полных колебаний.
6.Определить величины моментов инерции J0 и JS.
7.Составить отчёт с пояснениями.
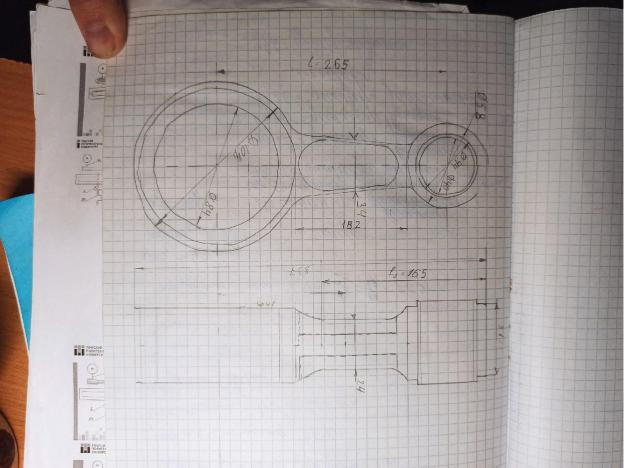
Рис. 1 Эскиз шатуна

Определение массы упрощенных звеньев
m = V ∙
Заменяем крепления полыми цилиндрами и основание шатуна заменяем параллелепипедом. Объем большого полого цилиндра
1 = |
|
∙ |
∙ ( 2 |
− 2) = 3,14 ∙ 0,036 ∙ |
0,0582−0,042 |
= 4,99 ∙ 10−5 м3 |
||
4 |
|
|||||||
|
|
|
|
|
|
|
|
|
Объем малого полого цилиндра |
|
|
|
|||||
2 = |
|
∙ |
∙ ( 2 |
− 2) = 3,14 ∙ 0,036 ∙ |
0,1042−0,0842 |
|
= 106 ∙ 10−6 м3 |
|
|
||||||||
4
Объем параллелепипеда
3 = ∙ ∙ = 0,182 ∙ 0,036 ∙ 0,024 = 0,0002 м3
Общий объем
= 1 + 2 + 3 = 0,003 м3
Плотность материала примем равную плотности стали = 7900 мкг3 Найдем массу каждого звена
Находим массу большого полого цилиндра
1 = 1 ∙ = 0,84 кг
Находим массу малого полого цилиндра
2 = 2 ∙ = 0,394 кг Находим массу параллелепипеда
3 = 3 ∙ = 1,242 кг
Масса Упрощенного шатуна
= 1 + 2 + 3 = 2,47 кг
Вес звена
= ∙ = 24,29 Н
Определим центр тяжести
|
|
|
|
|
|
∑ |
∙ |
|
|
∙ + |
∙ |
0,394 ∙ 0,024 + 1,242 ∙ 0,265 |
|
|||||||
|
= |
|
|
|
= |
2 |
3 |
|
= |
|
|
= 0,1 м |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
1 + 2 + 3 |
2,47 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Определим полярные моменты фигур: |
|
|||||||||||||||||||
|
= |
1 |
|
(3 2 |
+ 3 2 |
+ 2) = |
0,84 |
(3 ∙ 0,0522 + 3 ∙ 0,0422 + 0,0362) = 1,029 ∙ |
||||||||||||
|
|
|
|
|||||||||||||||||
1 |
12 |
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
||||
10−3 кг ∙ м2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
= |
2 |
(3 2 |
+ 3 2 |
+ 2) = |
0,394 |
(3 ∙ 0,0292 + 3 ∙ 0,0022 + 0,0362) = 0,17 ∙ |
|||||||||||||
|
|
|||||||||||||||||||
2 |
12 |
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||

10−3 кг ∙ м2
3 = 123 ( 2 + 2) = 1,24212 (0,0342 + 0, 1822) = 3,56 ∙ 10−3 кг ∙ м2
Найдем полярный момент:
= ( 2 + 2. ∙ 2) + ( 1. + 1. ∙ 2) + ( 3 + 3 ∙ ) = (0,17 ∙ 10−3 + 0.394 ∙ 0,12) + (1,029 ∙ 10−3 + 0.84 ∙ 0,042) + (3,56 ∙ 10−3 + 1,242 ∙ 0,161) =
0.21 кг ∙ м2
Результаты по определению периода колебаний и величин моментов инерции привести в таблицах:
Таблица 2 – Определение периода колебаний
|
Время |
20 |
Период |
|
Среднее значение |
|
№ опыта |
|
периода |
||||
колебаний, с |
|
колебаний, с |
|
|||
|
|
|
колебаний, c |
|||
|
|
|
|
|
||
1 |
t1=31.77 |
|
T1=t1/20=1,59 |
|
ср = |
|
2 |
t2=31.75 |
|
T2= t2/20=1,59 |
|
|
|
|
1+ 2+ 3 |
=1.59 |
||||
3 |
t3=31.72 |
|
T2= t3/20=1,59 |
|
3 |
|
|
|
|
||||
|
|
|
|
|||
Таблица 3 - Определение величины моментов инерции
|
Ls, |
|
|
|
|
|
2 |
|
∙ 2, кг |
|
|
= |
2 |
|
∙ |
|
= − ∙ 2, |
||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
m, кг |
|
|
Тср, с |
|
|
|
, м2 |
|
|
0 |
|
4 2 |
|
|
0 |
|
|||||
см |
4 2 |
|
кг ∙м2 |
||||||||||||||||||
|
|
|
|
|
|
|
∙м2 |
|
|
|
|
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
, кг ∙м |
|
|
|
|||||
2,5 |
18.1 |
|
1.59 |
|
0.064 |
0.0811 |
|
0.281 |
|
|
|
0.1995 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
− |
|
|
|0.1995 − 0.21| |
|
|
|
|
|
||||||||
|
∆ |
= |
а |
|
|
|
∙ 100% = |
|
|
|
|
|
|
∙ 100% = 7.13 % |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
0.21 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вывод: в данной лабораторной работе ознакомились с методикой экспериментального определения центра тяжести и момента инерций тела, имеющего ось вращения, не проходящую через центр тяжести. Расхождение в величинах моментов инерций, определение аналитическим путём и экспериментальным составила 7,13 %, что обусловлено упрощениями при определении геометрических параметров простых фигур, из которых состоит данное тело.
