ЛР2

Цель работы:анализвозможностей корреляционныхметодов выделения сигнала из шума и измерения его параметров

Выполнение работы.

В качестве решаемой задачи рассмотрим задачу измерения высоты полета самолета. Самым простым способом будет послать вертикально вниз короткий радиоимпульс и измерить при помощи корреляционной функции задержку импульса, отраженного от земли. Для этого, при помощи zeros(n,m), создаем такие импульсы из длинной нулевой последовательности присвоением группе выбранных отсчетов некоторого значения (амплитуды импульса).

При помощи команды conv(X,Y) которая для выполнения свертки

(скольжения по τ )предварительно увеличит вдвое длину вектора Y, построим(τ). Такой способ измерения высоты полета имеет 2 серьезных недостатка:

малаяпомехозащищенность(можнопойматьчужойимпульс)ипологаяформа(τ), не позволяющая гарантировать точность определения задержки при

наличии шума. Проверим, как изменится вид (τ),, если посылать более сложный

сигнал из двух или трех импульсов.

X=zeros (1,1000);

Y=zeros (1,1000);

X(1:100)=4;

Y(301:400)=2;

figure(1);

plot(conv(X,Y));

grid;

X(200:300)=4;

Y(501:600)=2;

figure(2);

plot(conv(X,Y));

grid;

Из случайной последовательности rand(1,m), логической операцией сравнения с порогом x > P создадим еще более сложный сигнал, в котором нет

n = rand (1,200); s1 = n>0.75;

s2 = (s1-0.5)*2;

y = zeros(1,10000); y(301:500) = s2;

R = zeros(1,1000); for i = 1:800

R(i) = s2*(y(i:i+199))';

end; R(801:1000) = 0;

figure(3);

plot(R);

grid;

x = ones(1,200); x(120:160) = 0; s2 = (s1-0.5)*2;

y = zeros(1,10000); y(301:500) = s2+x; C = zeros(1, 1000); for i = 1:800

C(i) = (s2-mean(s2))*(y(i:i+199)-mean(y))'; end;

figure(4);

plot(C);

grid;

Наложим на принятый сигнал шум с соотношением SNR 3÷ 10 дБ. Определим минимальное соотношение SNR , при котором еще возможно измерение задержки.

%Задание 3

x = ones(1,100); x(15:85) = 0;

r = randn (1,1000); r(401:500) = r(401:500) + x; for i = 1:900

R(i) = x*(r(i:i+99))';

end

figure(5);

plot(R);

grid;

x = ones(1,100); x(11:91) = 0;

r = randn (1,1000); r(401:500) = r(401:500) + x; for i = 1:900

R(i) = x*(r(i:i+99))';

end

figure(6);

plot(R);

grid;

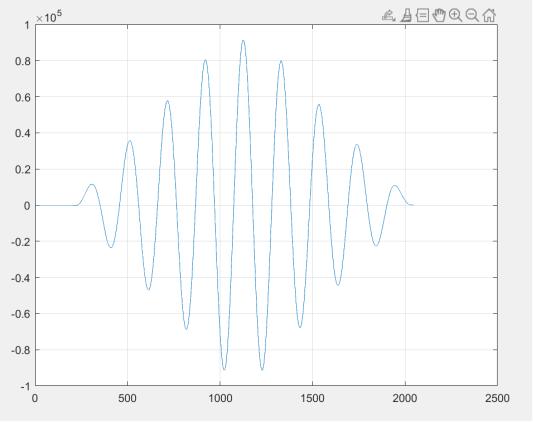
В качестве посылаемого сигнала возьмем отрезок синусоиды, наложим шум и построим (τ) .

%Задание 4

D = 15;

E = 5;

KP1 = 5; NFFT = 1024;

for t = 1:NFFT

ishod(t) = D*sin(2*pi*KP1*t/NFFT);

end

for k = 200: NFFT

p(k) = D*sin(2*pi*KP1*k/NFFT); o(k) = E*randn(size(NFFT)); w(k) = p(k) + o(k);

end

D = conv(ishod, w);

figure(7);

plot(D);

grid;

Выводы:

В данной лабораторной работе, нами был произведен анализ возможностей корреляционных методов выделения сигнала из шума, а так же измерения его же параметров.

Познакомились со скалярным произведением, с положением автокорреляции и основными методами проведения анализа выведения сигнала из шума.